Расчеты и моделирование магнитных полей для системы «кольца Гельмгольца – соленоид» проводились при проектировании и создании комплекса для проверки магнитометров инклинометра. Данный комплекс [1, 4] позволяет осуществлять проверку магнитометров инклинометра непосредственно на буровых площадках нефтегазовых месторождений.
Целью работы является подтверждение возможности создания однородного магнитного поля заданной величины в ограниченном геометрическими размерами установки объеме.
Общий вид комплекса представлен на рис. 1.
Комплекс состоит из установки 1 для базирования на ней проверяемого инклинометра 5, блока связи 2 с компьютером 3, соединительных кабелей и источника питания установки 4. Для работы с комплексом подходит любой персональный компьютер. Система «кольца Гельмгольца – соленоид» служит для создания постоянного направленного магнитного поля известной величины, с помощью которого осуществляется проверка магнитометров инклинометра.
Расчет колец Гельмгольца
Кольцами Гельмгольца называется система из двух одинаковых тонких катушек, расположенных соосно на расстоянии, равном их радиусу. В пространстве между катушками получается поле высокой однородности [2].
Суммарный модуль магнитного поля может быть получен из закона Био-Савара –Лапласа:
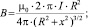 (1)
(1)
где µ0 = 1,257·10–6 Гн/м; I – ток, протекающий по виткам катушек колец, в амперах; R – радиус катушки, в метрах; х – расстояние по оси катушек, в метрах.
Катушки состоят из N витков. Общий ток N∙I.
Для системы двух колец Гельмгольца выражение магнитной индукции в геометрическом центре примет вид:
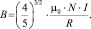 (2)
(2)
Магнитное поле, создаваемое кольцами Гельмгольца, в каждой точке продольной оси Х вычисляется по формуле:
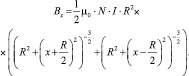 (3)
(3)
Магнитометры инклинометра помещены в цилиндрический корпус диаметром 30 мм на расстоянии 10 мм друг от друга и расположены ортогонально. Длина самого магнитометра 28 мм. Исходя из этого, необходимо создать кольца Гельмгольца и соленоид таких размеров, магнитное поле которых будет равномерным в объеме, вдвое превышающем объем, занимаемый чувствительными элементами.
Исходя из технических требований к изделию, кольца Гельмгольца и соленоид должны питаться от одного источника, максимальный ток которого не должен превышать 0,3 А. Максимальный диаметр колец 300 мм. Диаметр используемого намоточного провода равен 0,45 мм. Считать рабочей зону, в которой погрешность максимального однородного магнитного поля не превышает 1 %. Такая погрешность допустима для осуществления проверки работоспособности магнитометров инклинометра.
Имея исходные данные, по формуле (2) можно вычислить число витков намоточного провода на каждом кольце:
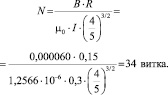 (4)
(4)
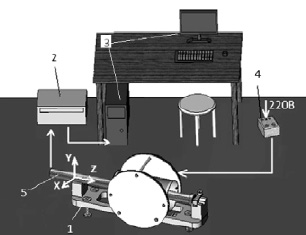
Рис. 1. Общий вид установки
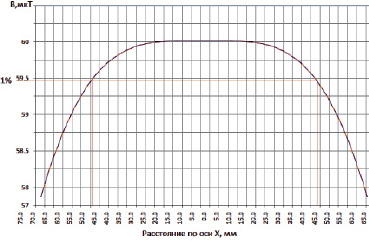
Рис. 2. Распространение магнитного поля в центре колец Гельмгольца вдоль оси Х
Сопротивление системы из 2-х колец:
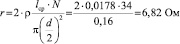 , (5)
, (5)
где ρ = 0,0178 Ом·мм²/м – удельное сопротивление меди; lср = π∙D∙n – длина провода в одном кольце. Действующее напряжение на концах намоточного провода колец определяется:
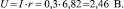 (6)
(6)
Расчетные значения индукции магнитного поля, созданного кольцами Гельмгольца вдоль оси Х, представлены на рис. 2. Зона максимального однородного магнитного поля с погрешностью в 1 % по оси Х составляет 90 мм.
Расчет соленоида
Диаметр соленоида должен быть максимальным и помещаться между кольцами Гельмгольца.
Исходные данные: радиус катушки Rк = 0,145 м; действующий ток I = 0,3 А; длина катушки lк = 0,3 м; диаметр провода dп = 0,00045 м; индукция магнитного поля соленоида В = 0,000060 Тл.
Напряженность магнитного поля:
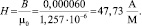 (7)
(7)
Выражение для расчета напряженности магнитного поля соленоида:
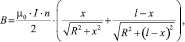 (8)
(8)
где В – индукция создаваемого магнитного поля, Тл; I – сила тока, А; n – число витков на единицу длины, n = N/l; R – радиус соленоида, м; l – длина соленоида, м; x – координата точки на оси соленоида.
Индукция магнитного поля внутри соленоида [2], в середине продольной оси, то есть при x = l/2 вычисляется как:
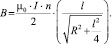 (9)
(9)
Из формулы (9), имея известные данные магнитной индукции, силы тока и геометрических размеров соленоида, можно найти требуемое число витков намоточного провода:
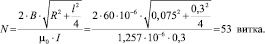 (10)
(10)
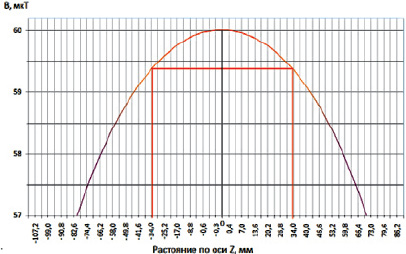
Рис. 3. Распространение магнитного поля в центре соленоида вдоль оси Z
Шаг намотки провода на соленоид:
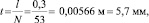 (11)
(11)
где t – шаг намотки провода, мм.
Сопротивление соленоида определяется, как
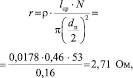 (12)
(12)
где dп – диаметр провода, м; ρ – удельное сопротивление меди 0,0178 Ом·мм²/м; Действующее напряжение определяется:
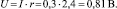 (13)
(13)
Расчетные значения индукции магнитного поля, созданного соленоидом вдоль оси Z, представлены на рис. 3.
Зона максимального однородного магнитного поля с погрешностью в 1 % по оси Z составляет 34 мм от центра соленоида в разные стороны.
Компьютерное моделирование магнитных полей
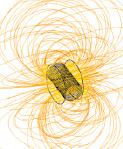
Моделирование магнитных полей, создаваемых системой «кольца Гельмгольца – соленоид», производилось в среде «Comsol» [3]. Расчет магнитного поля выполнялся в модуле «Magnetic Fields (mf)» [5]. Данные геометрических размеров, величины протекающих токов и количества витков использовались те же, что и при аналитическом расчете, а также, согласно техническому заданию, на разработку комплекса для проверки магнитометров инклинометра. Для более подробной визуализации распространения магнитных силовых линий в системе «кольца Гельмгольца – соленоид» представлены в упрощенном виде. Так как кольца Гельмгольца и соленоид включаются поочередно, то сначала моделируется работа соленоида, а затем работа колец Гельмгольца. На рис. 4, а показано распространение магнитных силовых линий в соленоиде.
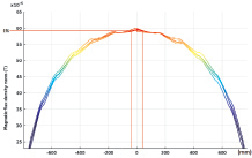
Представленная на рис. 4, б, зависимость показывает, что зона максимального однородного магнитного поля с погрешностью, не превышающей 1 %, составляет 33 мм в обе стороны от центра соленоида по оси Z.
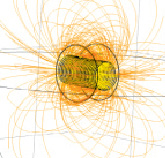
На рис. 5, а, показано распространение магнитных силовых линий поля при работе колец Гельмгольца.
 а
а
 б
б
Рис. 4. а – распространение магнитных силовых линий в соленоиде; б – величина магнитной индукции соленоида в зависимости от координаты точки, лежащей на продольной оси Z
 а
а
 б
б
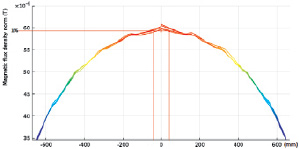
Рис. 5. а – распространение магнитных силовых линий в кольцах Гельмгольца; б – величина магнитной индукции колец Гельмгольца в зависимости от координаты точки, лежащей на продольной оси Х
Представленная на рис. 5, б, зависимость показывает, что зона максимального однородного магнитного поля с погрешностью, не превышающей 1 %, составляет 40 мм в обе стороны от центра колец Гельмгольца по оси X.
Заключение
Результаты аналитического моделирования показывают расхождения с графиками зависимости величины магнитного поля от координаты точки по осям соленоида и колец Гельмгольца, полученными при моделировании в среде Comsol. Расхождение результатов моделирования в среде Comsol с расчетными значениями для областей пространства, где магнитное поле однородно, не превышает для соленоида 3 %, а для колец Гельмгольца 12 %. Это связано с тем, что при использовании катушек колец Гельмгольца с большим количеством витков вторая производная при разложении в ряд Тейлора не равна нулю для пар витков, находящихся на расстоянии, отличном от R/2 вдоль оси Х, относительно геометрического центра системы. Вследствие чего неоднородность магнитного поля увеличивается. Расчеты и моделирование магнитных полей для системы «кольца Гельмгольца – соленоид» при заданных геометрических размерах и электрических параметрах питания системы показывают, что при позиционировании магнитометров проверяемого инклинометра в центре системы осуществлять проверку магнитометров инклинометра в полевых условиях возможно.
Рецензенты:
Дмитриев В.С., д.т.н., профессор НИ ТПУ, г. Томск;
Бориков В.Н., д.т.н., директор института неразрушающего контроля НИ ТПУ, г. Томск.
Работа поступила в редакцию 09.02.2015.
Библиографическая ссылка
Гормаков А.Н., Ульянов И.А. РАСЧЕТ И МОДЕЛИРОВАНИЕ МАГНИТНЫХ ПОЛЕЙ, СОЗДАВАЕМЫХ СИСТЕМОЙ «КОЛЬЦА ГЕЛЬМГОЛЬЦА – СОЛЕНОИД» // Фундаментальные исследования. 2015. № 3. С. 40-45;URL: https://fundamental-research.ru/ru/article/view?id=37081 (дата обращения: 05.03.2026).



