Активация растворных и бетонных смесей, а также составляющих их компонентов является одним из действенных технологических приемов, позволяющих целенаправленно регулировать свойства изделий на их основе [1, 2].
Анализ теоретических исследований и моделирование процессов воздействия электромагнитного поля на природную воду затворения растворных и бетонных смесей на основе цементного вяжущего позволяют утверждать, что на определенном этапе процесса их структурообразования имеется возможность активно влиять на технологические, структурные и физико-технические свойства получаемого материала [3, 4].
В этой связи разработка математической модели процесса активации природной воды затворения с целью управления качеством композиционного материала является актуальной задачей современного материаловедения.
Получение воды затворения с заданными параметрами и обеспечение стабильных и высоких результатов ее активации возможно при применении высокоточных техники и технологий, связанных с распространением электромагнитных волн. Аппараты и устройства, направленные на генерацию электромагнитных волн, часто должны соответствовать множеству критериев под определенную для этих аппаратов задачу. В связи с этим решение начально-краевых задач для трехмерного волнового уравнения является актуальным.
Классическая постановка начальной задачи для трехмерного волнового уравнения в положительном полупространстве будет иметь вид
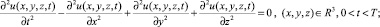 (1)
(1)
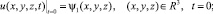 (2)
(2)
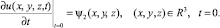 (3)
(3)
Используя отображение 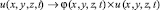 , где
, где 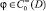 , можем получить постановку этой задачи в обобщенном смысле, в пространстве С.Л. Соболева. Рассмотрим выражение
, можем получить постановку этой задачи в обобщенном смысле, в пространстве С.Л. Соболева. Рассмотрим выражение
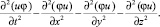
Тогда
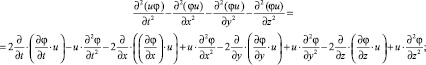
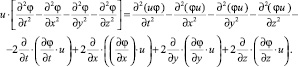
Интегрируя которое и используя формулу Гаусса – Остроградского по произвольной области D, будем иметь
 (4)
(4)
Если область D – все положительное полупространство (t > 0) с кусочно-гладкой границей S: 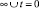 , а
, а 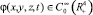 , то получим начальную задачу для трехмерного волнового уравнения в пространстве С.Л. Соболева.
, то получим начальную задачу для трехмерного волнового уравнения в пространстве С.Л. Соболева.
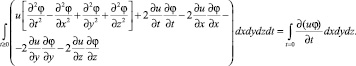 (5)
(5)
Выполним постановку начальной задачи для волнового уравнения на основе интегральных законов сохранения.
Пусть γ и γ′ – две непересекающиеся гиперповерхности в положительном полупространстве 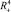 .
.
Определим функцию φ следующим образом:
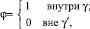
и функция φ гладким образом убывает от 1 до 0 вместе со своими производными 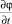 от γ до γ′.
от γ до γ′.
Рассмотрим левый интеграл из уравнения (5):
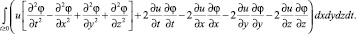
Учитывая свойства функции φ, этот интеграл будет иметь вид
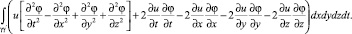
Заменяя интегрирование по полосе от γ до γ′ интегрированием по нормали и касательным направлениям к гиперповерхности γ, получим
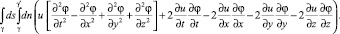
Ширину полосы γγ′ возьмем такой, чтобы можно было предположить, что
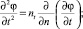
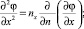
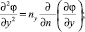
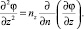
Так как nx = sx, ny = sy, nz = sz, nt = –st и sxds = dx, syds = dy, szds = dz, stds = dt, то получим
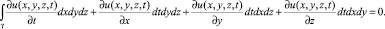
Таким образом, принимая во внимание правый интеграл из уравнения (5), получим обобщенную постановку начальной задачи для волнового уравнения на основе интегральных законов сохранения:
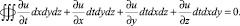
Реализуем явную разностную схему численного решения начально-краевой задачи для волнового уравнения.
Определим равномерную сетку с шагом h по пространственным переменным и с шагом τ по времени
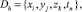
где xi = ih, yj = jh, zk = kh, tn = nτ, i = 0, ±1, ±2, ... , j = 0, ±1, ±2, ... , k= 0, ±1, ±2, ... , n= 0, 1, 2, ...
Для начальной задачи волнового уравнения
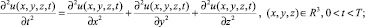 (6)
(6)
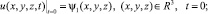 (7)
(7)
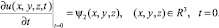 (8)
(8)
построим явную многомерную разностную схему:
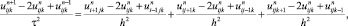
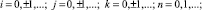 (9)
(9)
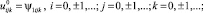 (10)
(10)
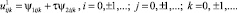 (11)
(11)
Из теории разностных схем известно, что невязка между точным решением задачи (6)–(7) и приближенным решением задачи (9)–(11) есть 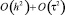 , а необходимое условие устойчивости разностной схемы (9)–(11) равняется
, а необходимое условие устойчивости разностной схемы (9)–(11) равняется 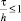 .
.
Реализуем метод расщепления численного решения начально-краевой задачи для волнового уравнения.
При решении многомерных задач объем вычислений методом сеток существенно возрастает. Для его снижения Н.Н. Яненко [5] предложил эффективный метод расщепления, который наряду с устойчивостью обладает свойством минимальности объема вычислений. Решение задачи (6)–(7) сводится к решению трех вспомогательных задач. Построим схему метода расщепления для решения задачи (6)–(7). Введем дифференциальный оператор A, такой, что
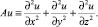
Тогда уравнение (6) можно записать в виде
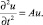
Оператор A является суммой трех операторов
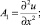
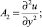
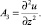
Рассмотрим три вспомогательные одномерные задачи.
Задача 1:
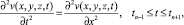 (12)
(12)
с начальными условиями
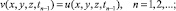 (13)
(13)
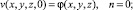 (14)
(14)
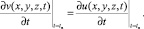 (15)
(15)
Задача 2:
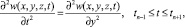 (16)
(16)
с начальными условиями
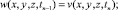 (17)
(17)
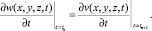 (18)
(18)
Задача 3:
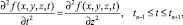 (19)
(19)
с начальными условиями
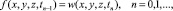 (20)
(20)
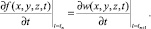 (21)
(21)
Поставленные задачи могут быть решены последовательно: сначала задача 1, потом задача 2, а затем задача 3.
Установим связь между функциями v(x, y, z, tn+1), w(x, y, z, tn+1), f(x, y, z, tn+1) и решением u(x, y, z, tn+1) исходной задачи на (n + 1) слое.
Пользуясь формулой Тейлора, для функции v(x, y, z, tn+1) получим соотношение
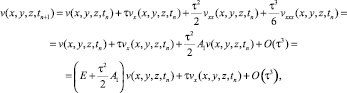 (22)
(22)
(23)
где E – единичный оператор.
Для функций w(x, y, z, tn+1) и f(x, y, z, tn+1) можно получить аналогичные выражения:
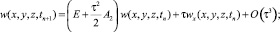 (24)
(24)
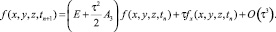 (25)
(25)
Воспользуемся дифференциальным условием (21) для задачи 3:
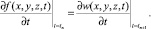
Пользуясь формулой Тейлора, получим соотношение
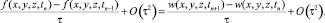
Учитывая условие (20), получим
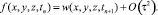
Аналогично
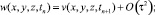
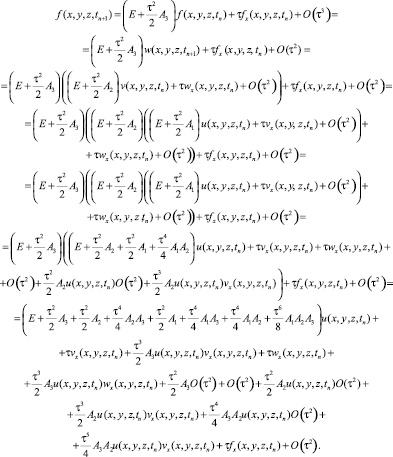
Рассмотрим выражение
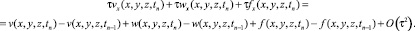
С учетом х начальных данных для вспомогательных задачи 1, задачи 2 и задачи 3 получим
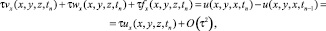
и так как
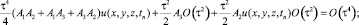
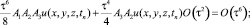
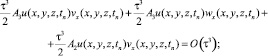
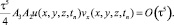 ,
,
получим
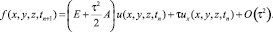 (26)
(26)
Следовательно, можем положить, что
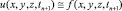 (27)
(27)
с соответствующей аппроксимационной оценкой.
Процесс решения исходной задачи с тремя пространственными переменными x, y, z заменен процессом решения трех задач с одной пространственной переменной в силу расщепления дифференциального оператора A на сумму трех операторов A1 + A2 + A3.
Очевидно, что метод расщепления не увеличивает погрешность по пространственным переменным x, y, z. Покажем, что и по времени t аппроксимационная оценка имеет тот же порядок, что и при прямом разностном методе.
Для каждой задачи (1, 2, 3) построим явные разностные схемы на той же сетке, что и для исходной многомерной задачи:
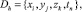
где xi = ih, yj = jh, zk = kh, tn = nτ, i = 0, ±1, ±2, ... , j = 0, ±1, ±2, ... , k= 0, ±1, ±2, ... , n= 0, 1, 2, ... .
Рассмотрим задачу 1.
Заменим производную vtt(xi, yj, zk, tn) её разностной аппроксимацией. Пользуясь формулой Тейлора, получим следующие соотношения:
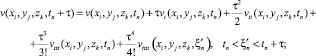 (28)
(28)
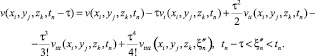 (29)
(29)
Сложим (28) и (29) и выразим vtt(xi, yj, zk, tn).
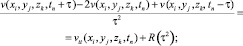 (30)
(30)
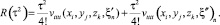 (31)
(31)
Аналогично получим аппроксимацию для vxx(xi, yj, zk, tn).
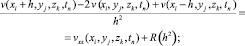 (32)
(32)
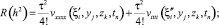
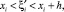
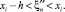 (33)
(33)
Из (31) и (32) получим
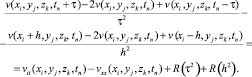 (34)
(34)
Оценим внутреннюю невязку 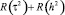 .
.
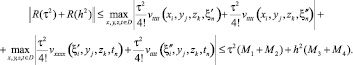 (35)
(35)
Пусть 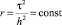 , тогда получим
, тогда получим
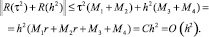 (36)
(36)
Таким образом получаем, что разностная схема (34) аппроксимирует исходную задачу 1 со вторым порядком аппроксимации по τ.
Начальное условие 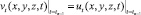 задачи 1 можно представить в следующем виде:
задачи 1 можно представить в следующем виде:
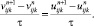 (37)
(37)
Тогда разностная схема для задачи 1 будет иметь следующий вид:
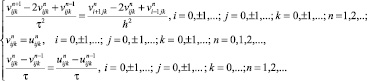 (38)
(38)
Аналогично для вспомогательных задач 2 и 3 соответственно получим
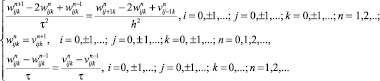 (39)
(39)
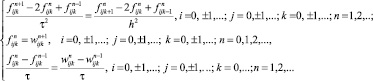 (40)
(40)
Разностные схемы (38), (39) и (40) аппроксимируют соответствующие им задачи со вторым порядком аппроксимации по h и τ.
Для доказательства устойчивости каждой из разностных схем воспользуемся спектральным признаком Неймана.
Рассмотрим разностную схему (38) для задачи 1:
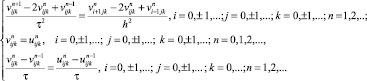
Определим начальное условие в виде трехмерной гармоники, зависящей от трех вещественных параметров α, β, γ:
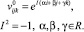 (41)
(41)
Тогда решение задачи 1 при начальном условии (41) имеет вид
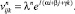 (42)
(42)
Функция 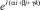 является собственной функцией разностного оператора
является собственной функцией разностного оператора
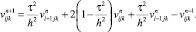 (43)
(43)
λ(α, β, γ) – соответствующее собственное число разностного оператора.
Подставив это выражение в разностную схему, получим
 (44)
(44)
Поделим полученное равенство на 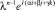 , получим
, получим
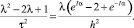 (45)
(45)
Обозначим 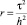 и заметим, что
и заметим, что
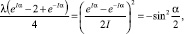 (46)
(46)
получим
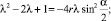 (47)
(47)
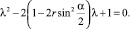 (48)
(48)
Для выполнения условия устойчивости необходимо, чтобы спектр разностного оператора λ(α, β, γ) лежал в единичном круге, т.е. 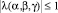 .
.
Произведение корней этого уравнения по теореме Виета равно единице. Если дискриминант
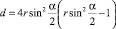 (49)
(49)
квадратного уравнения отрицателен, то корни λ1(α, β, γ) и λ2 (α, β, γ) комплексно-сопряженные и равны единице по модулю.
В случае r < 1 дискриминант остается отрицательным при всех α. В этом случае спектр заполняет часть единичной окружности.
В случае r = 1 спектр заполняет всю окружность.
При r > 1, по мере увеличения α от 0 до π, корни λ1(α, β, γ) и λ2(α, β, γ) двигаются из точки λ = 1 по единичной окружности: один по часовой, а другой против часовой стрелки соответственно и сходятся в точке λ = –1. Затем один из корней перемещается по вещественной оси из точки λ = –1 влево, а другой вправо, т.к. они вещественны и λ1∙λ2 = 1.
Условие устойчивости выполнено при r ≤ 1.
Проведя аналогичные подстановки и преобразования для разностных схем (45) и (46), соответствующих вспомогательным задачам 2 и 3, получим
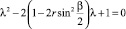 – для разностной схемы (45),
– для разностной схемы (45),
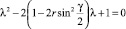 – для разностной схемы (46).
– для разностной схемы (46).
По рассуждениям, аналогичным для (41)–(49), получаем, что условие устойчивости для разностных схем (39) и (40) выполняется также при r ≤ 1.
Рецензенты:Камбург В.Г., д.т.н., профессор кафедры «Информационно-вычислительные системы», Пензенский государственный университет архитектуры и строительства, г. Пенза;
Монастырев П.В., д.т.н., профессор, директор института архитектуры, строительства и транспорта, Тамбовский государственный технический университет, г. Тамбов.
Работа поступила в редакцию 06.03.2015.
Библиографическая ссылка
Бояркин Д.И., Фомичев В.Т., Ерофеев В.Т., Емельянов Д.В., Матвиевский А.А. МОДЕЛИРОВАНИЕ ПРОЦЕССОВ АКТИВАЦИИ ПРИРОДНОЙ ВОДЫ ЗАТВОРЕНИЯ БЕТОНОВ В ЭЛЕКТРОМАГНИТНОМ ПОЛЕ // Фундаментальные исследования. 2015. № 2-6. С. 1157-1165;URL: https://fundamental-research.ru/ru/article/view?id=36997 (дата обращения: 31.12.2025).



