Рассмотрим один из каналов управления объектом эргатической системы [2…5]. Предположим, что оператор является безинерционным звеном, формирующим сигнал x(t) ошибки системы. Тогда при гипотезе независимости каналов для каждого канала управления систему можно представить в виде, изображенном на рис. 1.
Приведем внутреннюю помеху к выходу. Тогда структурную схему можно представить в виде, изображенном на рис. 2.
Если внутренние помехи не зависят от внешних возмущений, то импульсная переходная функция разомкнутой системы H(t, ξ) определится решением интегрального уравнения:
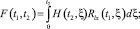
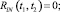
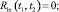
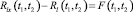 .
.
Определив решением интегрального уравнения
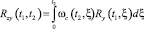
импульсную передаточную функцию цепи обратной связи ωc(t, ξ) и решив уравнение
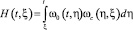
относительно ω0(t, ξ), можно определить импульсную передаточную функцию объекта.
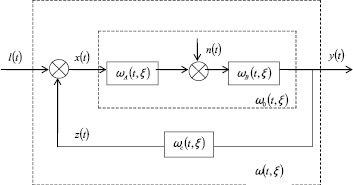
Рис. 1. Одноканальная система: l(t) – входное возмущение (или программа); x(t) – сигнал ошибки системы (исполнительный сигнал), z(t) – сигнал обратной связи; n(t) – помеха; ω(t, ξ) – импульсная переходная функция системы; ω0(t, ξ) – импульсная переходная функция объекта; ωc(t, ξ) – импульсная переходная функция обратной связи; ωA(t, ξ) – импульсная переходная функция части объекта, где действием помехи можно пренебречь
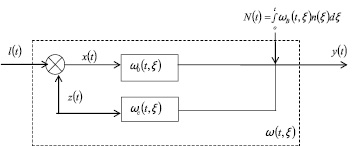
Рис. 2. Приведение помехи к выходу
В частном случае стационарной системы, находящейся в режиме непрерывного функционирования, на вход которой поступает стационарное возмущающее воздействие, будем иметь
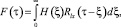
где
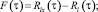
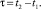
Или в частотной области
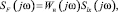
откуда
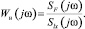
Здесь
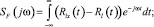
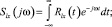
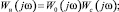
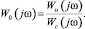
В случае необходимости импульсная передаточная функция системы ω(t, ξ) может быть определена решением интегрального уравнения
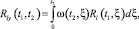
или решением интегрального уравнения Вольтера второго рода:
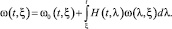
Отметим, что
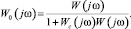
Заметим, что передаточная функция системы по отношению к помехе n(t) равна
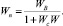
Для стационарной системы уравнение имеет вид
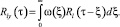
Имеет место аналогичная формула для цепи обратной связи:
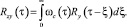
В частотной области:
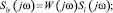
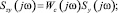
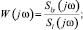
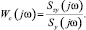
Как видим, знания действующих на систему внутренних помех n(t) для определения W(jω), W0(jω), Wc(jω) не потребовалось; с учетом l(t) = x(t) – z(t) видим, что для их определения не требуется и знания l(t). Достаточно иметь регистрацию сигнала ошибки x(t), сигнала обратной связи z(t), выходного сигнала y(t).
В соответствии со структурной схемой на рис. 1
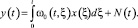
Откуда
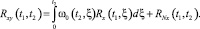
В случае стационарной системы с входным стационарным сигналом отсюда следует
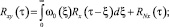
это дает возможность проверки гипотезы о наличии неявной «паразитной» обратной связи между входным и выходным сигналами разомкнутой системы.
В самом деле, эта формула показывает, что при наличии обратной связи входной сигнал x(t) коррелирован как с выходным сигналом объекта y(t), так и с приведенной помехой. При этом RNx(τ) зависит от величины этой связи, а знак – от знака обратной связи системы.
Для проверки гипотезы о наличии неявной обратной связи достаточно сравнить функции Rx(τ), Rxy(τ) при τ ≤ 0. Если в системе существует отрицательная обратная связь, то будет наблюдаться спад ординат левой ветви взаимной корреляционной функции Rxy(τ) по сравнению с ординатами Rx(τ) для тех значений τ, где RNx(τ) ≠ 0 (τ ≈ 0), и тем резче, чем больше RNx(τ). При наличии положительной обратной связи вместо спада в этой области будет иметь место возрастание взаимной корреляционной функции Rxy(τ).
Таким образом, при неизвестной структуре системы процедура диагностики ее функционирования сводится к:
– вычислению корреляционных функций Rx(τ), Rxy(τ);
– проверке исследуемой системы на отсутствие (наличие) обратной связи;
– оценке внутренних помех;
– оценке вычисленных характеристик.
При этом алгоритм нахождения частотной характеристики объекта по данным нормальной эксплуатации определяется последовательностью формул:
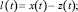
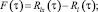
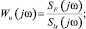
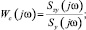
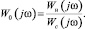
При отрицательной единичной обратной связи получим

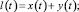
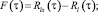
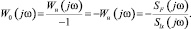
Формулы для определения W0(jω) справедливы как при наличии, так и при отсутствии внутренних помех (например, атмосферных – при проектировании авиационных тренажеров).
Методики прошли апробацию при разработке тренажных и обучающих комплексов для подготовки операторов транспортных систем [1, 6, 7].
Рецензенты:Родионов Ю.В., д.т.н., профессор, заведующий кафедрой «Эксплуатация автомобильного транспорта», декан автомобильно-дорожного института, Пензенский государственный университет архитектуры и строительства, г. Пенза;
Кошев А.Н., д.х.н., профессор кафедры «Информационно-вычислительные системы», Пензенский государственный университет архитектуры и строительства, г. Пенза.
Работа поступила в редакцию 02.03.2015.
Библиографическая ссылка
Будылина Е.А., Гарькина И.А., Данилов А.М., Дулатов Р.Л. СТРУКТУРНАЯ И ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ СЛОЖНЫХ ЭРГАТИЧЕСКИХ СИСТЕМ // Фундаментальные исследования. 2015. № 2-5. С. 919-922;URL: https://fundamental-research.ru/ru/article/view?id=36956 (дата обращения: 12.03.2026).



