Задачи о полях давления при фильтрации жидкости составляют основу теории массопереноса в пористой среде, поскольку они имеют большое практическое значение для нефте- и газодобычи, гидрогеологии, экологии и т.д. [1]. Здесь особое место имеет задача о фильтрации в неоднородных анизотропных пластах в силу разнообразия условий и практической значимости. Ниже показано, что важные аналитические зависимости могут быть успешно получены на основе новых модификаций асимптотических методов, возможности которых при специальном выборе формального параметра асимптотического разложения пока мало реализованы. При этом возникает необходимость построения нулевого и первого коэффициентов разложения, погранслойных функций и оценочных выражений для остаточного члена. Полученный таким образом нулевой коэффициент разложения описывает осредненные значения физических параметров. Построение первого коэффициента требует добавочных условий, которые получены на основе тривиального решения осредненной задачи для остаточного члена. В силу этого соответствующие выражения для нулевого и первого приближения названы «в среднем точными» [2–4].
Развитый авторами настоящей статьи метод уже позволил построить новые сравнительно простые аналитические решения фундаментальных задач подземной гидродинамики [2–4]. Здесь же иллюстрируется применение метода к важнейшей для нефтепромыслового дела квазистационарной задаче, в ограниченном по высоте стоке в неоднородной анизотропной среде. Аналогичная модельная задача ранее была рассмотрена в [3], в [5] построено решение модельной задачи для радиального течения в нулевом приближении для постоянного отбора. В отличие от указанных работ здесь осуществлена постановка и представлено решение задачи с реальными (имеющими физический смысл) коэффициентами в уравнениях и граничных условиях, проведено сопоставление первого асимптотического приближения с точным решением.
Постановка задачи для линейного течения при постоянной депрессии
Пусть среда представлена тремя областями с плоскими границами раздела, покрывающий и подстилающий пласты считаются слабо проницаемыми в горизонтальном направлении, средняя область толщины 2h является хорошо проницаемой и в горизонтальном, и в вертикальном направлениях. Для простоты течение предполагается линейным. Пусть окружающие породы являются сильно анизотропными, и в них преобладает вертикальная проницаемость в сравнении с горизонтальной настолько, что можно пренебречь членом со второй производной по горизонтальной координате в уравнении для окружающей среды. Далее предположим, что свойства подстилающих и покрывающих пластов идентичны. В соответствии с этим постановку задачи можно упростить, воспользовавшись условием симметрии относительно оси пласта.
Дальнейшее упрощение рассматриваемой задачи без заметных искажений основных изучаемых особенностей достигается путем использования так называемого квазистационарного приближения, широко используемого для упрощения исследований нестационарных процессов. Прямоугольную систему координат выберем таким образом, чтобы ось абсцисс была направлена вдоль горизонтального пласта, ось Oz – ей перпендикулярна.
Математическая постановка гидродинамической задачи в таких предположениях включает уравнение пъезопроводности в верхнем пласте
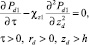 (1)
(1)
стационарное уравнение в центральном пласте
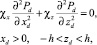 (2)
(2)
условие симметрии в центре пласта
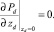 (3)
(3)
Начальное условие может быть записано только для окружающей среды
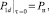 (4)
(4)
поскольку уравнение пъезопроводности в центральном пласте является стационарным. На границе раздела сред заданы равенства давлений и потоков
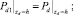 (5)
(5)
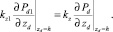 (6)
(6)
Для случая постоянной депрессии давление на левой границе полагается постоянным
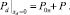 (7)
(7)
В силу граничных условий (5) и (7) давление в пласте зависит от времени параметрически, и его значение при τ = 0 обозначено Pн.
Перейдем далее к безразмерным координатам, используя соотношения
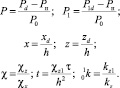 (8)
(8)
С учетом формул (8) уравнения (1), (2) примут вид
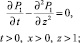 (9)
(9)
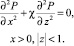 (10)
(10)
Граничные, начальные условия и условия сопряжения при этом не изменяются
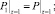
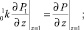
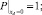
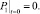 (11)
(11)
Предполагается, что решение является регулярным на бесконечности, т.е. при устремлении пространственных координат в бесконечность искомое решение, а при необходимости и его производная, обращаются в нуль.
Параметризация задачи
Рассмотрим более общую задачу, полученную введением произвольного асимптотического параметра ε, путем замены 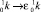 . Так как коэффициент пъезопроводности пропорционален проницаемости, этот параметр появится перед первой и второй производными по z как в уравнениях, так и в граничных условиях задачи. Отметим, что решение исходной задачи может быть получено из решения параметризованной задачи при ε = 1. Задача (9)–(11) является, таким образом, частным случаем более общей параметризованной, содержащей формальный параметр асимптотического разложения ε как в уравнении для пласта, так и в условиях сопряжения
. Так как коэффициент пъезопроводности пропорционален проницаемости, этот параметр появится перед первой и второй производными по z как в уравнениях, так и в граничных условиях задачи. Отметим, что решение исходной задачи может быть получено из решения параметризованной задачи при ε = 1. Задача (9)–(11) является, таким образом, частным случаем более общей параметризованной, содержащей формальный параметр асимптотического разложения ε как в уравнении для пласта, так и в условиях сопряжения
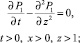 (12)
(12)
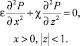 (13)
(13)
Граничные, начальные условия и условия сопряжения при этом не изменяются
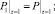
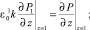
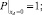
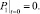 (14)
(14)
Будем искать решение задачи (12)–(14), представляя функцию давления P каждой из областей асимптотической формулой по параметру ε
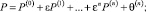
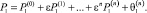 (15)
(15)
Подставив выражения (15) в (12)–(14) и сгруппировав слагаемые по степеням параметра разложения ε, получим:
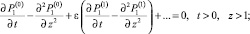 (16)
(16)
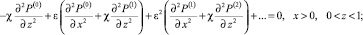 (17)
(17)
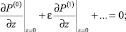
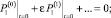 (18)
(18)
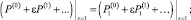
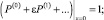 (19)
(19)
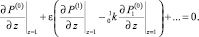 (20)
(20)
Формально устремим ε к нулю в уравнении (17), получим 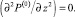 Воспользовавшись условием (18), задачу для определения нулевого приближения приведем к следующему виду:
Воспользовавшись условием (18), задачу для определения нулевого приближения приведем к следующему виду:
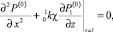
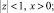 (21)
(21)
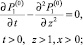 (22)
(22)
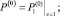

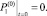 (23)
(23)
Отметим, что рассматриваемая задача относится к неклассическими представляется смешанной, поскольку уравнение для пласта не является параболическим. Кроме того, это уравнение содержит следы производных из внешних областей.
Непосредственным интегральным усреднением исходной задачи нетрудно убедиться, что (21)–(23) представляет задачу для осредненных по толщине центральной зоны значений давления. Это определяет физический смысл нулевого коэффициента разложения или нулевого приближения и практическую важность его определения, поскольку поиском осредненных значений в подобного рода задач чаще всего и ограничиваются.
Применяя интегральные преобразования Лапласа – Карсона по переменной t, вместо (22) получим обыкновенное дифференциальное уравнение, и решение задачи в нулевом приближении представится как
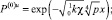
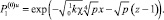 (24)
(24)
Применяя обратное преобразование Лапласа – Карсона [6], получим:
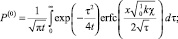
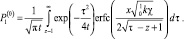 (25)
(25)
Задача для первого коэффициента
Из (26)–(27) следуют выражения для первого коэффициента разложения
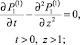 (26)
(26)
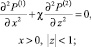 (27)
(27)

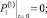
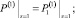 (28)
(28)
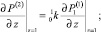
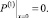 (29)
(29)
Уравнение (27) и выражение (29) содержат коэффициенты первого и второго порядков разложения, поэтому соответствующая задача является зацепленной. Расцепление проводится с помощью процедуры, описанной в [7].
Задача (26)–(29) имеет только тривиальное решение. Ниже показано, что для получения единственного решения задачи для первого коэффициента разложения второе условие (29) следует ослабить и заменить нелокальным средне- интегральным
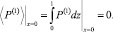 (30)
(30)
При добавлении этого условия задача для первого коэффициента разложения имеет единственное решение. При этом осредненная задача для остаточного члена имеет только нулевое решение, что позволяет назвать построение «в среднем точным» асимптотическим решением [7]. Решение для первых коэффициентов представится как
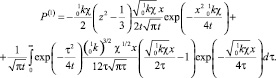 (31)
(31)
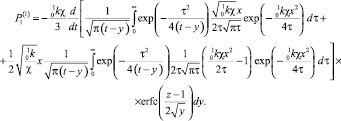 (32)
(32)
Решение (31) состоит из двух частей: первая часть с сомножителем t – нормируемая или функциональная, поскольку определяет зависимость от вертикальной координаты; вторая часть с сомножителем x – ненормируемая. Ненормируемая часть определяется частным решением неоднородного уравнения. Для практических приложений более важна функциональная часть, поскольку чаще всего в расчетах преследуется построение профилей физических величин, когда определяется разность между значением в любой точке и значением при фиксированном z.
Приведенные выше выражения обеспечивают детальную зависимость поля давления от вертикальной координаты в зоне осреднения. Однако главное значение первого коэффициента разложения или его физический смысл заключается в том, что он позволяет получить стационарные вертикальные профили давления.
Построение погранслойных функций
Первый коэффициент асимптотического разложения не обращается в нуль при х = 0 вопреки требованиям исходной задачи (29). Этот недостаток решения устраняется построением погранслойной функции. Для этого введем растянутую переменную 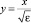 и искомое решение разобьем на две части: регулярную (15) и погранслойную
и искомое решение разобьем на две части: регулярную (15) и погранслойную
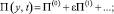
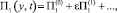 (34)
(34)
а затем выделим задачи для коэффициентов погранслойных разложениий различных порядков. Задача для погранслойных коэффициентов нулевого порядка имеет только тривиальное решение П(0) = 0 и 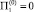 . Решение задачи для первых погранслойных коэффициентов имеет следующий вид:
. Решение задачи для первых погранслойных коэффициентов имеет следующий вид:
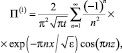
0 < z < 1, x > 0. (35)
Полученное выражение для П(1) позволяет определить граничное условие в задаче для первого погранслойного коэффициента в окружающей среде 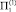 . Окончательное решение этой краевой задачи имеет вид
. Окончательное решение этой краевой задачи имеет вид
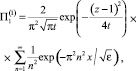 ,
,
z > 1, x > 0. (36)
Выражения (35), (36) представляют искомые погранслойные функции и вместе с нулевыми (25) и первыми (31), (32) коэффициентами определяют искомое асимптотическое решение исходной задачи. При этом значение погранслойных функций заключается в том, что оно описывает стабилизацию или развитие стационарного профиля по координате х.
Точное решение квазистационарной задачи
Рассматриваемая задача удобна тем, что можно построить ее точное решение в пространстве изображений. Если воспользоваться преобразованием Лапласа – Карсона по переменной t (⇒ p) и синус-преобразованием Фурье по координате х (⇒ s), тогда параметризованная задача (12)–(14) запишется как
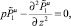 z > 1, t > 0, (37)
z > 1, t > 0, (37)
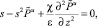 0 < z < 1, x > 0, (38)
0 < z < 1, x > 0, (38)
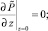
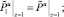
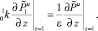 (39)
(39)
Решение задачи (39)–(39) в пространстве изображений имеет вид
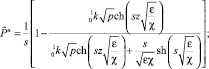 (40)
(40)
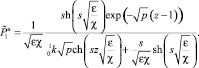 (41)
(41)
Оригиналы решений для преобразования Лапласа – Карсона представляются в форме
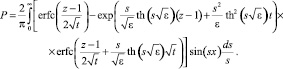 (42)
(42)
Выражение (42) позволяет определить нулевой и первый коэффициенты разложения
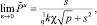 (43)
(43)
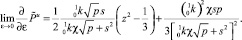 (44)
(44)
Нетрудно убедиться, что выражение (43) является синус-преобразованием нулевого коэффициента (25), а (44) – первого (31). Такое совпадение нулевого и первого коэффициентов свидетельствует о корректности концепции «в среднем точного» асимптотического решения исходной задачи, представленного выше.
Выводы
Применение асимптотического метода позволяет построить относительно простые аналитические формулы для детальных расчетов и существенно уточнить развитые ранее модели фильтрации в неоднородных пластах. При этом коэффициенты точного в среднем асимптотического решения и разложения точного решения по асимптотическому параметру совпадают. В силу этого примененный в работе «точный в среднем» асимптотический метод можно рассматривать как некоторый универсальный практически важный алгоритм поиска стационарных или квазистационарных решений краевых задач в ограниченных подобластях, что является отражением глубинных внутренних свойств асимптотических разложений краевых задач сопряжения математической физики.
Рецензенты:
Шулаев Н.С., д.т.н., профессор, заведующий кафедрой информатики, математики и физики, филиал ФГБОУ ВПО УГНТУ, г. Стерлитамак;
Мустафина С.А., д.ф.-м.н., профессор, заведующий кафедрой математического моделирования Стерлитамакского филиала БашГУ, г. Стерлитамак.
Работа поступила в редакцию 28.01.2015
Библиографическая ссылка
Михайлов П.Н., Михайлов А.П., Филиппов И.М., Кульсарина Н.А. ЛИНЕЙНАЯ МОДЕЛЬ ПОЛЯ ДАВЛЕНИЯ ПРИ ПОСТОЯННОЙ ДЕПРЕССИИ В НЕОДНОРОДНОМ ОРТОТРОПНОМ ПОРИСТОМ ПЛАСТЕ // Фундаментальные исследования. 2015. № 2-1. С. 42-48;URL: https://fundamental-research.ru/ru/article/view?id=36614 (дата обращения: 07.03.2026).



