Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Батракова Г.М. 1 Бояршинов М.Г. 1 Ташкинова И.Н. 1

---

1 ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет»

Методами прикладной математики обработаны результаты экспериментальных исследований биоразложения нитробензола и анилина в модельных почвах. Способ очистки и восстановления почв территорий промышленного назначения, загрязненных в результате аварийных проливов, основан на внесении сообществ живых организмов, способных к биодеградации загрязняющих веществ, и на стимуляции почвенной микрофлоры. Для интенсификации аборигенной микрофлоры почв с целью очистки от амино- и нитроароматических соединений использована биомасса активного ила, адаптированного к веществам-загрязнителям в лабораторных и промышленных условиях. Выполнена аппроксимация данных по результатам экспериментов, что позволило уточнить оптимальную дозу ила, позволяющую достичь максимальной скорости биоразложения, определить расчетный расход биомассы ила для ликвидации загрязнений почв с известной концентрацией и глубиной проникновения по почвенному профилю. Предложена методика аппроксимации зависимости концентрации загрязняющего вещества в почве от дозы внесенного ила и времени выдержки.

Статья в формате PDF

1250 KB

загрязнение почв

нитробензол

анилин

активный ил

аппроксимация экспериментальных данных

поиск оптимальных параметров

1. Балабанов Д.С., Бояршинов М.Г. Рассеяние отработанных газов автотранспорта над городской территорией. – Saarbrucken: LAP LAMBERT Academic Publishing, 2012. – 113 с.

2. Батракова Г.М., Бояршинов М.Г., Ташкинова И.Н., Чудинова Я.Н. Исследование процесса биоразложения нитробензола в почвенных условиях // Вестник Казанского технологического университета. – 2014. – Т.17, № 23. – С. 199–202.

3. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – М.: Наука, 1973. – 720 с.

4. Калиткин Н.Н. Численные методы. – М.: Наука, 1978. – 512 с.

5. Кузнецов А.Е., Градова Н.Б.. Научные основы экобиотехнологии: учебное пособие для студентов. – М.: Мир, 2006. – 504 с.

6. Швецова И.Н. Обеспечение экологической безопасности при ликвидации зданий и сооружений химических предприятий и рекультивации нарушенных территорий (на примере анилинового производства): автореф. дис. ... канд. техн. наук. – М., 2013. – 18 с.

7. Швецова И.Н., Батракова Г.М., Зайцева Т.А. Обоснование использования активного ила для биологической рекультивации почв, загрязненных ароматическими аминами (анилином) // Теоретическая и прикладная экология. – 2013. – № 1. – С. 16–20.

8. Швецова И.Н., Бояршинов М.Г., Батракова Г.М. Обоснование метода биологической рекультивации территории, загрязненной аминоароматическими соединениями // Экология урбанизированных территорий. – 2013. – № 1. – С. 87–92.

9. Shvetcova I., Batrakova G. Research of ecological hazard of building materials after exploitation in aggressive industrial environment // Proc. 12th Int. Multidisc. Sc. «Geoconference and Expo – Modern management of mine producing, geology and environmental protection, SGEM 2012», Bulgaria. – Sofia, 2012. – Vol. V. – P. 693–698.

Перспективными способами очистки почв промышленного назначения являются биотехнологические методы, основанные на внесении сообществ живых организмов, способных к биодеградации загрязняющих веществ, и на стимуляции естественной микрофлоры почв.

Известным методом стимуляции микрофлоры загрязненных почв является использование осадков сточных вод, отвечающих требованиям безопасного использования для биологической рекультивации нарушенных земель (согласно ГОСТ Р 54534-2011). В большей степени в литературе описаны результаты исследований и применения методов биологической рекультивации нефтезагрязненных земель, территорий горно-обогатительных комбинатов и участков излива стоков угольных шахт, рекультивации полигонов захоронения коммунальных отходов и др. Для широкого спектра токсичных соединений, к которым относятся и нитро- и аминоароматические соединения, методы восстановления почв не разрабатывались.

Внесение в загрязненные почвы осадков сточных вод благоприятно из-за поступления больших объемов метаболически активных микроорганизмов и присутствие макро- и микроэлементов, важных для биологических процессов в почве. В то же время токсичные соединения в загрязненных почвах снижают активность биомассы живых организмов, поэтому для рекультивации нарушенных земель могут быть использованы организмы, устойчивые к специфическому загрязнителю [5]. При очистке сточных вод анилино-красочных производств в г. Перми и г. Березники длительное время использовался метод интенсивной биологической очистки, разработанный учеными политехнического института (г. Пермь), института органических полупродуктов и красителей (НИИОПиК, г. Москва) и заводскими лабораториями. Для разработки способа очистки почвы, загрязненной анилином и нитробензолом, проведены исследования снижения концентрации веществ-загрязнителей в модельных пробах почвы при внесении активного ила из системы биологической очистки промстоков предприятия [6, 7]. Методами прикладной математики обработаны результаты экспериментальных исследований биоразложения нитробензола и анилина и получены уточненные значения оптимальной дозы реагента на основе активного ила, адаптированного к веществам-загрязнителям, с целью увеличения эффективности процесса биоразложения.

Экспериментальное исследование

Для моделирования технологических проливов на землю подготовлены модельные пробы почвы:

а) 10 до 1000 мг нитробензола на 1 кг почвы;

б) 100 до 10 000 мг анилина на 1 кг почвы.

В образцы вносились дозы активного ила и комплексное минеральное удобрение (N:Р:К в соотношении 2:1:1). Исследуемые образцы почвы выдерживались от 3 до 5 дней в условиях постоянной влажности почвы, сохраненияе стабильной температуры +10 °С, рыхления почвы. Остаточное содержание загрязняющих веществ определялось фотометрическим (на основе ПНД Ф 14.1:2.252-08) и газохроматографическим (МУК 4.1.1207-03) методами. В качестве безопасного уровня загрязнения принимались значения рекомендованного допустимого содержания для земель промышленного назначения: для нитробензола в почве – 0,26 мг/кг, анилина – 17 мг/кг [2, 9]. Результаты экспериментов представлены в табл. 1 и 2.

Таблица 1

Результаты экспериментальных исследований снижения концентрации нитробензола в образцах почвы

Таблица 2

Результаты экспериментальных исследований снижения концентрации анилина в образцах почвы

Примечание. * 1.5ф – фоновая проба почвы (имеющая фоновый уровень содержания вещества-загрязнителя).

Результаты экспериментов показали, что при дозе внесения ила 2 г/м2 концентрация анилина за 15 суток снижается до 90–99 % масс. Большие дозы внесения ила (до 4 г/м2) оказались менее эффективны.

Методика построения математической модели

Для анализа разложения загрязняющих почву веществ (нитробензола и анилина) путем внесения активного ила целесообразно использовать аппарат математического анализа, позволяющий описать результаты экспериментальных измерений концентрации нитробензола и анилина в почве непрерывными функциями; с использованием полученных зависимостей можно определить условия получения максимальной скорости снижения концентрации указанных веществ в почве. Использование математического аппарата позволяет получать наиболее полные данные об исследуемых процессах; математическое моделирование экономично, значительно более информативно в сравнении с экспериментальными методами, позволяет делать превентивные оценки для ситуаций, натурное моделирование которых экономически нецелесообразно или опасно [1].

Эволюционные процессы, аналогичные рассматриваемым (радиоактивный распад, разложение вещества, снижение концентрации и прочие), как правило, описываются с использованием экспоненциальных зависимостей. Анализ данных натурных измерений концентрации анилина в почве (рис. 1) показывает, что рассматриваемый процесс также можно описать экспоненциальной зависимостью вида

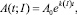(1)

где t – время, независимая переменная; I – доза вносимого активного ила, параметр; k(I) определяет зависимость изменения концентрации вещества (нитробензола или анилина) в почве от дозы активного ила. Функцию k(I) целесообразно представить разложением по степеням I дозы активного ила, то есть в виде частичной суммы ряда Тейлора:

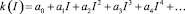(2)

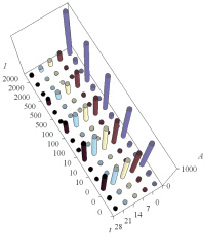
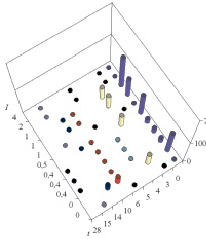
а б

Рис. 1. Данные натурных измерений концентрации в почве нитробензола (а) и анилина (б) (A, мг/кг) в зависимости от дозы ила (I, мг/кг) и времени t (сутки)

В разложении (2) в первом приближении следует ограничиться первыми тремя слагаемыми (квадратичная аппроксимация):

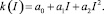(3)

Таким образом, зависимость концентрации каждого из рассматриваемых веществ в почве представляется выражением

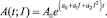(4)

где A0, a0, a1, a2 – параметры, подлежащие определению на основе экспериментальных данных, уникальные для каждого из рассматриваемых случаев. Очевидно, что при t = 0 из выражения (4) следует

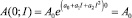(5)

то есть коэффициент A0 играет роль начальной концентрации вещества в почве. Для определения остальных параметров a0, a1, a2 используется метод наименьших квадратов [4], хорошо зарекомендовавший себя при аппроксимации данных экспериментальных исследований. Для удобства преобразований в дальнейшем используются приведенные значения,

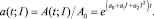(6)

Далее выражение (6) логарифмируется,

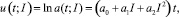(7)

и строится функция трех переменных, определяющая отклонение зависимости u(t, I) от логарифмов экспериментальных значений Aexp(t; I) концентрации рассматриваемого вещества в почве:

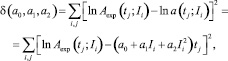(8)

где Ii – экспериментальные значения дозы активного ила; tj – фиксированные в эксперименте моменты времени. Согласно алгоритму метода наименьших квадратов коэффициенты a0, a1, a2 определяются из условия минимума отклонения u(t, I) зависимости (7) от логарифмических значений Aexp(t; I), то есть минимума квадратичной функции δ(a0, a1, a2). Согласно необходимому признаку экстремума [3] минимум функции (8) определяется из условий

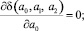
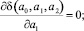
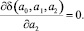(9)

Дифференцирование выражения (8) приводит к системе линейных алгебраических уравнений относительно коэффициентов a0, a1, a2:

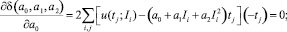
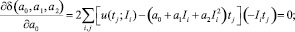
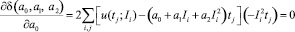(10)

или

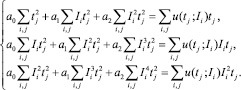(11)

Формирование системы уравнений (11) с использованием данных натурных измерений и ее решение позволяет определить коэффициенты a0, a1, a2 и, с учетом начального значения концентрации A0 загрязнителя в почве, сформировать в явном виде зависимость (4) содержания рассматриваемого вещества в почве от времени и дозы вносимого активного ила.

Дополнительным вопросом исследования является установление оптимальной дозы активного ила, обеспечивающей наибольшую скорость снижения концентрации загрязняющих почву нитробензола и анилина. Скорость изменения концентрации загрязнителя в почве определяется производной по времени функции (4):

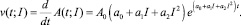(12)

Полученное выражение (12) зависит от времени t; целесообразно определить такое значение дозы активного ила, которая гарантирует наибольшую скорость с самого начала процесса разложения, то есть начиная с t = 0,

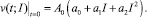(13)

Для определения максимального значения скорости разложения загрязнителя выражение (13) дифференцируется по параметру I,

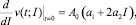(14)

и полученное выражение (14), согласно необходимому признаку экстремума [3], приравнивается к нулю,

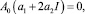(15)

что приводит к линейному уравнению

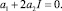(16)

Отсюда следует

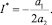(17)

Зависимость от времени (4) концентрации загрязнителя при условии экстремальной скорости разложения принимает вид

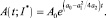(18)

Проверка знака второй производной,

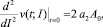(19)

позволяет проверить вид экстремума скорости (максимальное или минимальное значение достигается при найденном значении I*).

Концентрация нитробензола в почве

Для выявления основных закономерностей влияния активного ила на интенсивность разложения нитробензола в почве на основе экспериментальных данных (табл. 1, рис. 1, а) с использованием изложенной методики построена зависимость вида (4), аппроксимирующая изменение концентрации этого соединения в зависимости от времени наблюдения и доз вносимого ила (рис. 2).

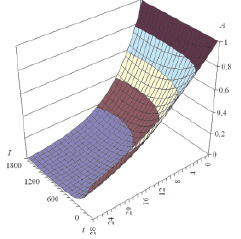
Рис. 2. Аппроксимация данных измерений концентрации нитробензола в почве (A, мк/кг) в зависимости от дозы ила (I, мк/кг) и времени (t, сут)

Решение системы уравнений (11) позволило определить значения искомых коэффициентов:

a₀ = –0,443316∙10^–1; a₁ = –0,153705∙10^–3;

a₂ = 0,526673∙10^–7.

Это означает, что зависимость (4) концентрации нитробензола в почве представляется выражением

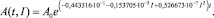(20)

Решение уравнения (15) позволяет определить искомое значение дозы активного ила, доставляющее максимальное значение скорости снижения концентрации:

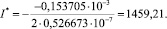
При найденном значении I* выражение (18) принимает вид

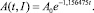
Поскольку вторая производная (19) аппроксимирующей функции

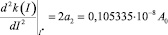
положительна, скорость изменения концентрации нитробензола в почве, определяемая выражением (13), при найденном значении I* достигает своего минимального (в частности, отрицательного) значения. Но это как раз и означает, что скорость убывания функции (19) при I* будет наибольшей.

По результатам натурного эксперимента для разложения всех опробованных проливов нитробензола в техногенных почвах наиболее эффективной признана доза 2000 мг/кг (2 г/кг) сухого вещества почвы, что близко к теоретически найденному значению 1459 мк/кг. При внесении такой дозы ила достигалось разложение нитробензола с его остаточным содержанием по истечении 28 дней 1,4–5,5 % масс. Расчетное количество комплексных минеральных удобрений, необходимых при использовании такой дозы ила, составило 4,8 мг/кг сухого вещества почвы.

Концентрация анилина в почве

Аналогичное исследование выполнено для аппроксимации на основе экспериментальных данных (табл. 2, рис. 1, б) зависимости концентрации анилина от дозы активного ила и времени наблюдения [7, 8]. Разработанная методика позволила построить зависимость вида (4), аппроксимирующая изменение концентрации анилина в почве (рис. 3).

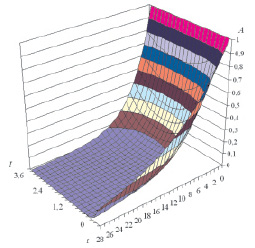
Рис. 3. Аппроксимация данных измерений концентрации анилина в почве (A, мк/кг) в зависимости от дозы ила (I, мк/кг) и времени (t, сут)

Решение системы уравнений (11) дает значения коэффициентов

a₀ = –0,076630; a₁ = –0,246321;

a₂ = 0,052660,

то есть зависимость (4) концентрации нитробензола в почве представляется выражением

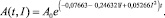(21)

Значение дозы активного ила, доставляющее максимальное значение скорости изменения концентрации, равно

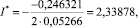
что позволило преобразовать выражение (19) к виду

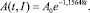
Поскольку вторая производная (17) аппроксимирующей функции

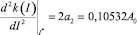
также положительна, скорость изменения концентрации нитробензола в почве при найденном значении I* достигает своего минимального (отрицательного) значения, следовательно, скорость убывания функции (19) при I* будет наибольшей.

Выводы

Методом аппроксимации зависимости концентрации загрязняющего вещества в почве от времени выдержки и дозы внесения активного ила определены условия достижения максимальной скорости убывания концентраций нитробензола и анилина. Результаты, полученные при математическом моделировании, соответствуют величинам оптимальных доз биомассы активного ила, выявленным в экспериментальных исследованиях.

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 13-05-96025 р_урал_а.

Рецензенты:

Май И.В., д.б.н., профессор, зам. директора по научной работе, ФНЦ медико-профилактических технологий управления рисками здоровью населения, г. Пермь;

Максимова С.В., д.т.н., профессор, зав. кафедрой «Архитектура и урбанистика» ПНИПУ, г. Пермь.

Работа поступила в редакцию 28.12.2014.

Библиографическая ссылка