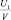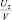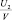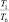Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Ляпцев С.А. 1 Степанова Н.Р. 2

---

1 ГБОУ ВПО «Уральский государственный горный университет»

2 ФГАОУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н.Ельцина»

Ударные механические нагрузки являются эффективным способом воздействия на объект в целях его разрушения или передачи этого воздействия по какой-то другой системе взаимосвязанных элементов. Статья посвящена теоретическим расчетам коэффициента полезного действия ударного механизма, в схему которого входит промежуточная масса. При расчетах применены общие теоремы динамики при ударе, в том числе теорема об изменении количества движения точки и теорема об определении коэффициента восстановления. Показано, что в некоторых случаях промежуточная масса, выполняя роль волновода, принимает на себя часть ударной нагрузки и передает значительную энергию ударному инструменту. Рациональный путь уменьшения коэффициента передачи энергии при отдаче состоит во введении промежуточной подвижной массы между инструментом и ударником. Показано также, что коэффициент полезного действия ударного механизма существенно зависит от соотношения масс подвижных частей механизма. Получены оптимальные соотношения масс подвижных частей ударника.

Статья в формате PDF

404 KB

ударные механизмы

промежуточная подвижная масса

коэффициент восстановления

энергия удара

1. Вебер Г.Э., Ляпцев С.А. Дополнительные главы механики для горных инженеров. – Свердловск: УрГУ, 1989. – 200 с.

2. Горбунов В.Ф., Лазуткин А.Г., Ушаков Л.С. Импульсный гидропривод горных машин. – Новосибирск: Наука, 1986. – 197 с.

3. Ляпцев С.А. Научные основы разработки электромеханических ударных устройств горного производства: дис. … д-ра техн. наук. – Екатеринбург: УГГУ, 2002. – 157 с.

4. Ляпцев С.А., Степанова Н.Р. Экспериментальные исследования эффективности работы ударных устройств // Горный информационно-аналитический бюллетень (научно-технический журнал). – 2003. – № 8. – С. 149–150.

5. Пановко Я.Г. Введение в теорию колебаний и удара. – М.: Наука, 1989. – 264 с.

6. Ушаков Л.С., Котылев Ю.Е., Кравченко В.А. Гидравлические машины ударного действия. – М.: Машиностроение, 2000. – 416 с.

Ударные механические нагрузки являются эффективным способом воздействия на объект в целях его разрушения или передачи этого воздействия по какой-то другой системе взаимосвязанных элементов [1]. Использование устройств в исполнительных органах горных, строительно-дорожных и других машин открывает перспективу расширения области их применения в специфических условиях энергоемких процессов.

Изучение закономерностей разрешения горных пород предполагает выявление и создание таких условий, при которых процесс разрушения производителен и при наименьших затратах энергии. С увеличением скорости приложения нагрузки возрастают предел прочности материала и удельная работа разрушения. В связи с этим часто вводится понятие критической скорости смешения частиц породы при которой происходит ее разрушение [5]. Критические скорости для горных пород имеют тот же порядок, что и для металлов. Для достижения одной и той же кинетической энергии увеличение массы движущихся частей является более рациональным, чем соответствующее увеличение скорости. Вместе с тем наиболее важное значение имеет абсолютная величина работы удара независимо от того, получена ли она за счет увеличения массы или скорости. В этом смысле удачным является введение некоторыми исследователями (см., например, [2]) понятия динамической твердости, под которой понимается минимальное значение работы удара, необходимой для полного разрушения породы.

Существует несколько способов передачи энергии. Наиболее характерным для технологических машин является способ передачи энергии, реализуемый с помощью ударно-передающих систем [4].

Волновой способ передачи энергии имеет место в том случае, когда импульс давления производится взрывом, разрядом, гидравлическим ударом или другим методом в граничной от наружного объекта среде [6]. Кинематический способ импульсного нагружения основан на сообщении некоторому исполнительному устройству кратковременного ускорения, превышающего ускорение свободного падения в несколько раз.

Ввиду сложности учета всех факторов, влияющих на параметры волн напряжений в ударной системе, большинство исследователей предпочитают экспериментальные методы их определения, а не теоретические. Исследование взаимодействий породоразрущающего инструмента с массивом имеет важное практическое значение, так как позволяет не только изучить механику процесса, но и установить количественные зависимости между параметрами ударной нагрузки и глубиной внедрения инструмента в породу. Из сопоставления скоростных и силовых характеристик, приведенных в работе [2], следует, что при увеличении массы ударника адекватно изменяется продолжительность его взаимодействия с массивом. Характерным для силовой характеристики в данном случае является нарастающее изменение усилий от нуля до максимального значения. При этом колебания нагрузки на инструменте обусловлены в основном процессом разрушения горной породы.

Экспериментальные исследования ударной системы с промежуточным звеном, описанные в той же работе [2], показывают, что при определенном соотношении масс бойка и инструмента, если масса бойка меньше массы инструмента, удар с некоторой максимальной скоростью влечет остановку бойка. Таким образом, весь запас кинетической энергии реализуется на контакте боек ‒ промежуточное звено, и дальше в массив энергия передается по промежуточному звену, как по волноводу, в виде импульса напряжений. Система, в которой масса бойка больше массы инструмента, существенно изменяет форму силовой характеристики. В первый период происходит соударение бойка с промежуточным звеном (волноводом), поэтому на характеристике изменения силы выделяется значительно преобладающий по амплитуде головной импульс. Общая продолжительность взаимодействия инструмента с массивом включает также действие хвостовой части импульса, при этом продолжительность волнового возмущения в массиве равна сумме продолжительностей головного и хвостового импульсов, если до удара имеется достаточно плотный контакт инструмента с массивом. Волновое возмущение не равно этой сумме, если головной импульс не передается в массив из-за отсутствия предварительного контакта инструмента с породой. Таким образом, изменяя тип ударно-преобразующей системы, возможно влиять на характер силовой характеристики процесса, а следовательно, и эффективность передачи энергии в массив.

Представляется возможной теоретическая оценка коэффициента полезного действия (КПД) ударного механизма с промежуточной массой [3].

Обозначим через m1 – массу инструмента, а через m2 – массу ударника. В принятых обозначениях запишем выражение теоремы об изменении количества движения при ударе [1]:

m₁V = m₁U₁ + m₂U₂, (1)

где V – скорость инструмента в начале удара; U1 и U2 – скорости инструмента и промежуточной массы в конце первого и второго ударов.

По определению коэффициента восстановления k при ударе [5]

U₂ = –kV. (2)

Решая систему уравнений (1)–(2), получим

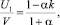(3)

где

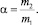(4)

При расчете скоростей и энергий полагаем, что удары происходят друг за другом (сначала 1–2, затем 2–3).

Величину передачи кинетической энергии при ударе оценим с помощью отношений

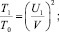
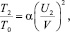(5)

где Т₀ – исходная кинетическая энергия, передаваемая на инструмент; Т₁, Т₂ – кинетическая энергия инструмента и ударника соответственно в конце удара.

Результаты расчетов по формулам (5) для стальных инструмента и ударника (k = 0,83) приведены в таблице.

Результаты определения отношений скоростей и энергий для механизма с промежуточной массой

Как следует из приведенных результатов, при

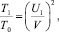
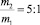(6)

коэффициент передачи энергии составит 0,47. После остановки ударника инструмент может нанести по нему второй удар, но уже с меньшей скоростью. При α < 1,2 инструмент после удара продолжает движение в ту же сторону, куда двигался и с меньшей скоростью. После этого инструмент возвращается назад, ударяя уже по корпусу механизма. Отдача (удар по корпусу механизма) всегда сопровождает технологический процесс разрушения горных пород. Однако следует подбирать такое соотношение подвижных масс, чтобы коэффициент передачи энергии при отдаче энергии был как можно меньше.

В качестве примеров расчета явления отдачи укажем некоторые из вариантов определения коэффициента передачи энергии. Из расчетов, приведенных выше, следует, что при α = 0,2 скорость инструмента уменьшится до

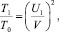U = 0,67V. (7)

Нанеся второй удар уже по неподвижному ударнику, инструмент изменит направление скорости, сократив ее величину до

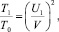U = kU1 = 0,55V. (8)

Коэффициент передачи энергии составит при отдаче

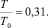(9)

При α = 0,6 скорость инструмента после первого удара составит 0,31V, а после второго удара – U = 0,67V. Таким образом, коэффициент передачи энергии составит всего T/Т0 = 0,07. Рациональный путь уменьшения коэффициента передачи энергии при отдаче состоит во введении промежуточной подвижной массы между инструментом и ударником.

Рецензенты:

Воротников В.И., д.ф.-м.н., профессор, заместитель директора по науке и инновациям, ФГБОУ ВПО «Нижнетагильский технологический институт (филиал) УрФУ» Министерства образования и науки Российской Федерации, г. Нижний Тагил;

Красовский А.Н., д.ф.-м.н., профессор, заведующий кафедрой информационных технологий и математического моделирования, ФГБОУ ВПО «Уральский государственный аграрный университет», г. Екатеринбург.

Работа поступила в редакцию 27.12.2014.

Библиографическая ссылка