Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Семенчин Е.А. 1 Титов Н.Г. 1 Кузякина М.В. 1 Лебедев К.А. 1

---

1 ФГБОУ ВПО «Кубанский государственный университет»

Некоторые реки Краснодарского края являются реками горного типа. Реки данного типа обладают крутым падением водотока (угол наклона течения) и площадью водосбора, отличающейся от рек равнинного типа своей подстилающей поверхностью. Такие особенности реки делают невозможным использование ранее разработанных математических моделей для рек горно-равнинного типа. В данной статье предлагаются две математические модели прогнозирования уровня воды в реках горного типа. Первая модель позволяет производить прогноз с помощью рассчитанного уравнения линейной регрессии, описывающего изменения уровня воды в русле горной реки Мзымта; другая – производить прогноз уровня воды, основываясь на математической модели созданной на основе нейронной сети архитектуры многослойного персептрона. Также в статье проведено сравнение полученных математических моделей.

Статья в формате PDF

604 KB

математическое моделирование

регрессионный анализ

метод наименьших квадратов

нейронные сети

прогнозирование

многослойный персептрон

метод обратного распространения

паводковые ситуации

1. Статистическое моделирование и прогнозирование [под ред C.A. Гранборга]. – М.: Финансы и статистика, 2000. – 383 с.

2. Ивченко Г.И., Медведев Ю.И. Математическая статистика: учеб. пособие для втузов. – М.: Высш. шк., 1984. – 248 с.

3. Крамер Г. Математические методы статистики. – М.: ир, 1975. – 375 с.

4. Титов Н.Г., Семенчин Е.А., Об оценке коэффициентов в уравнении линейной регрессии, описывающем изменения уровня воды в русле горной реки // Известия Кубанского государственного университета. Естественные науки. – 2013. – № 1(2). – С. 49–51.

5. Медведев В. С., Потемкин В.Г. Нейронные сети. – М.: Диалог МИФИ, 2002. – 496 с.

6. Осовский С. Нейронные сети для обработки информации. – М.: Финансы и статистика, 2002. – 344 с.

7. Титов Н.Г., Семенчин Е.А., Лебедев К.А., Прогноз уровня воды в реке горного типа с помощью нейронной сети имеющей архитектуру многослойного персептрона // Современные концепции научных исследований: матер. IV международной научно-практич. конф. (Москва, 25 июля 2014 г.). – М., 2014. – № 4 (2) – С. 149–152.

8. Халафян А.А. Статистический анализ данных. STATISTICA 6.0. – Краснодар: Изд-во КубГУ, 2003. – 191 с.

На территории Краснодарского края находится немало рек, которые следует отнести к рекам горного типа. В основном эти реки протекают в горных районах Сочи – Туапсе. Рекам такого типа свойственны высокая скорость течения и резкое изменение уровня воды в русле за счет обильных осадков, ледникового и снегового питания, что не так характерно для рек равнинного и горно-равнинного типов. Как показывают вычислительные эксперименты, методики, описывающие изменения уровня воды в руслах рек равнинного и горно-равнинного типов, не применимы для описания изменения уровня воды в руслах рек горного типа. В данной статье предлагается анализ двух математических моделей прогнозирования уровня воды в реках горного типа. Первая модель позволяет производить прогноз с помощью рассчитанного уравнения линейной регрессии, описывающего изменения уровня воды в русле горной реки Мзымта; другая – производить прогноз уровня воды, основываясь на математической модели, созданной на основе нейронной сети архитектуры многослойного персептрона.

Цель работы – апробировать ранее разработанную математическую модель прогноза уровня воды в реке горного типа на основе уравнения линейной регрессии на промежутке времени в один год; апробировать ранее разработанную математическую модель прогноза уровня воды в реке горного типа на основе построенной нейронной сети архитектуры многослойного персептрона на промежутке времени в один год; провести анализ полученных результатов методами математической статистики и на основе данного анализа выбрать математическую модель, высчитывающую наиболее приближенный к реальному значению будущий уровень воды в реке горного типа.

Оценка коэффициентов в уравнении линейной регрессии,
описывающем изменения уровня воды в русле горной реки

Предположим, что значения уровня воды в реке на момент времени ti совпадают со значениями функции [4].

(1)

где y(ti) – прогнозируемый уровень воды в створе данной реки в районе гидрологического поста, x1(ti–5), x1(ti–4), x1(ti–3), x1(ti–2), x1(ti–1) – уровень воды в моменты ti–5, ti–4, ti–3, ti–2, ti–1 соответственно, x2(ti–5), x2(ti–4), x2(ti–3), x2(ti–2), x2(ti–1) – количество осадков, выпавших в соответствующие моменты времени в окрестности русла горной реки. Пусть соотношение (1) определяет математическую модель процесса изменения уровня воды в реке горного типа.

Пусть функция (1) является линейной:

(2)

где a1, a2, a3, a4, a5, a6, a7, a8, a9, a10, b1 – некоторые постоянные.

На основе статистических данных, взятых из гидрологических бюллетеней за 2010 год по реке Мзымта, методами регрессионного анализа [1] были вычислены в статье [4] значения коэффициентов и свободного члена в (2) (табл. 1).

Согласно данным, приведенным в табл. 1, функция (2) (регрессионная модель) имеет вид

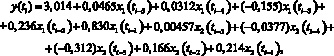(3)

Таблица 1

Значения коэффициентов и свободного члена в регрессионной модели (2)

Точность оценки прогноза значений y(ti) определяется числовыми значениями характеристик регрессионной модели (3), приведенными в табл. 2, коэффициентом детерминации [3]

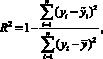(4)

и значением критерия Фишера [3]

(5)

где n – размер выборки (количество проведенных замеров); k – число коэффициентов модели (3); yi – наблюдаемое значение y(t);  – значение y(ti) вычисленное с помощью уравнения регрессии (3) в момент ti, i = 6, 7, ..., n;  – среднее значение y(ti), вычисленное на основе статистических данных.

Таблица 2

Характеристики регрессионной модели (2)

Если F превышает некоторое критическое значение Fкр, определяемое по таблице значений F-критерия Фишера при заданных n, k и заданной доверительной вероятности, а величина R2 близка к 1, то значение y(ti), вычисленное по формуле (3), с вероятностью, близкой к 1, совпадает с экспериментальными данными. Согласно статистическим данным и допущениям, указанным выше, Fкр = 10,534, α = 0,95, n = 545, k = 10, R2 = 0,97131498, F = 1808.

Так как F > Fкр (1808 > 10,534, т.е. значение F во много раз превышает Fкр), то с вероятностью 0,95 при стандартной ошибке σ = 10,217 значения y(ti) совпадают с реальными значениями y(ti), i = 6, 7, ..., n [2].

На рис. 1 приведены графики значений y(ti), построенные на основе статистических данных и значений регрессионной модели (3). Из этих графиков видно, что прогнозируемые с помощью (3) значения y(ti) несущественно отличаются от статистических данных.

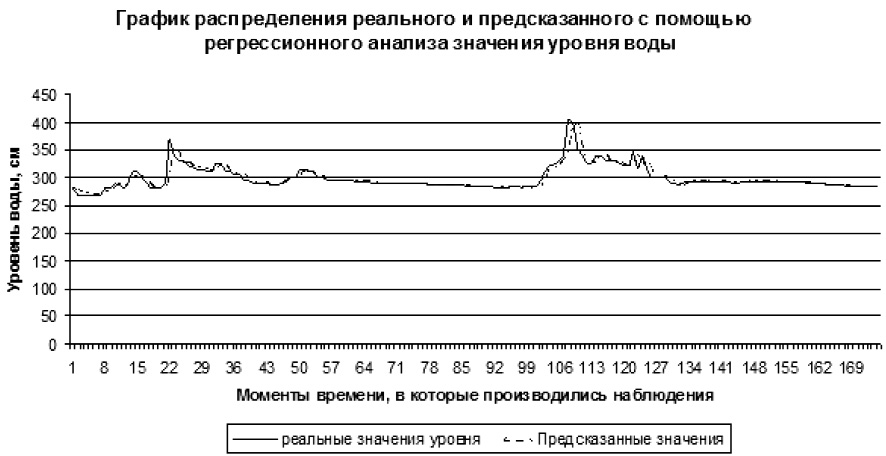
Рис. 1. Графики значений y(t), построенные
на основе статистических данных регрессионной модели (3)

Прогнозирование уровня воды в реке горного типа на основе нейронной сети, имеющей архитектуру многослойного персептрона

Для разработки нейронной сети, позволяющей построить прогноз уровня воды в русле горной реки, с архитектурой многослойного персептрона и последующего ее обучения были использованы статистические данные о метеоусловиях на гидрологическом посту, расположенном на реке Мзымта, предоставленные Краснодарским центром гидрометеорологии и мониторинга окружающей среды. Использовался пакет прикладных программ Statistica 6.1 [8].

Обучение производилось с помощью метода обратного распространения, основной идеей которого является распространение сигналов ошибки от выходов сети к её входам в направлении, обратном прямому распространению сигналов в обычном режиме работы.

Архитектура построенной согласно (1) нейронной сети для прогноза паводков в русле указанной реки определяется как многослойный персептрон (трехслойный), имеющий на первом слое 8 нейронов, на втором – 5, на третьем – 1 [7]. Данная архитектура представлена в виде упрощенной схемы на рис. 2.

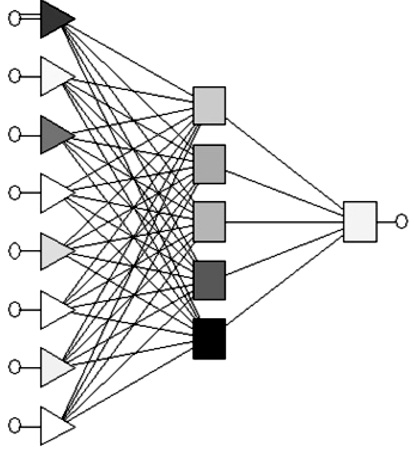
Рис. 2. Схема работы нейронной сети архитектуры трехслойного персептрона:
8 – входных сигналов, изображенных кругами; 8 – синапсов первого слоя, изображенных треугольниками; 5 – синапсов второго слоя, изображенных квадратами;
1 – синапс третьего слоя, изображенный прямоугольником; 1 – выходной сигнал, изображенный кругом

Таблица 3

Значения весов на слое 1

В каждый нейрон подаются входные значения xi с некоторой поправкой wi(xi), затем сумма w1(x1) + w2(x2) + w3(x3) поступает на передаточную функцию

f(w1(x1) + w2(x2) + w3(x3)),

где wi(xi), i = 1, 2, 3 принято называть соответственно входными дендритами и синапсами [5].

Описанная нейронная сеть использует алгоритм обучения обратного распространения, который использует несколько слоев нейронов, связанных между собой. Задача обучения нейронной сети сводится к нахождению функциональной зависимости y = f(x). Для сужения области поиска необходимых весов необходимо уменьшить функцию ошибки нейронной сети. Это достигается с помощью метода обратных квадратов [6]:

где dj – целевое значение j-го выхода; p – число нейронов в выходном слое.

Вторым этапом обучения нейронной сети являлось обучение методом градиентного спуска. Каждая итерация сопровождалась изменением веса по формуле [6]:

где η – параметр, определяющий скорость обучения.

Полученные в результате обучения веса представлены в табл. 3, 4.

Таблица 4

Значения весов на слое 2

Таблица 5

Характеристики нейронной сети

Для обучения описанной нейронной сети были использованы данные об уровне воды и количестве осадков в реке Мзымта за январь-декабрь 2010 года. Характеристики построенной нейронной сети приведены в табл. 5.

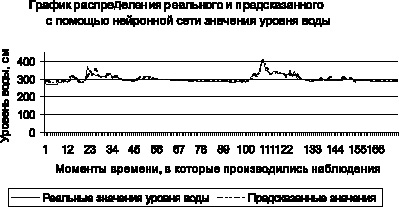
Рис. 3. Графики значений y(t), построенные
на основе статистических данных с помощью нейронной сети

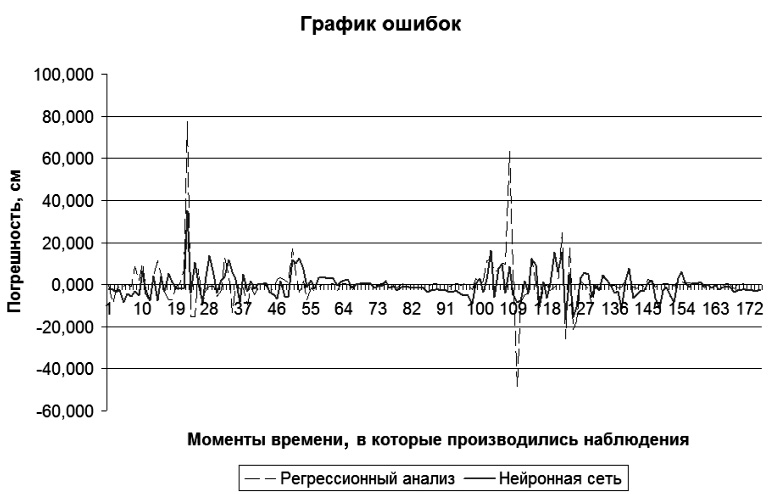
Рис. 4. График ошибок

На рис. 3 приведены графики значений y(t), построенные на основе статистических данных и значений, полученных с помощью нейронной сети. Из этих графиков видно, что прогнозируемые значения y(ti) несущественно отличаются от статистических данных.

Выводы

Сравнивая полученные результаты, можно сделать следующие выводы. Оба предложенных в статье метода дают адекватный результат. Однако метод, основанный на регрессионном анализе, показывает большую стандартную ошибку (10,21772 > 8,693615) по сравнению с методом, основанным на использовании нейросетевых технологий. Визуализация полученных результатов, представленная на рис. 1, 3, 4, подтверждает проведен-
ные расчеты.

Халафян А.А., д.т.н., профессор, ФГБОУ ВПО «Кубанский государственный университет», г. Краснодар;

Уртенов М.А.Х., д.ф.-м.н., зав. кафедрой прикладной математики, ФГБОУ ВПО «Кубанский государственный университет»,
г. Краснодар.

Работа поступила в редакцию 19.12.2014.

Библиографическая ссылка