Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Станкевич Ф.В. 1 Спицын В.Г. 1

---

1 ФГАОУ ВО «Национальный исследовательский Томский политехнический университет»

В данной статье рассматривается распознавание образов с применением нейронных сетей на примере распознавания музыкальных инструментов. Проблема распознавания звука музыкальных инструментов рассматривается во многих работах, но большинство из них используют большое количество признаков. Целью нашей работы является минимизация количества признаков при условии получения высокой точности распознавания. В качестве признаков используются мел-частотные кепстральные коэффициенты с применением метода главных компонент. Для классификации признаков используется нейронная сеть прямого распространения. Для обучения сети были рассмотрены два подхода: метод обратного распространения ошибки и нейроэволюционный алгоритм Enforced Subpopulations (ESP). Метод обратного распространения ошибки показал лучшие результаты. Данная работа посвящена распознаванию отдельно звучащих нот музыкальных инструментов, однако предложенный алгоритм показал хорошие результаты и при анализе сложных сигналов.

Статья в формате PDF

2235 KB

распознавание образов

музыкальные инструменты

мел-частотные кепстральные коэффициенты

метод главных компонент

нейроэволюция

1. Фадеев А.С. Идентификация музыкальных объектов на основе непрерывного вейвлет-преобразования. Диссертация, Томский политехнический университет, 2008 – 192 с.

2. Brown J.C. Computer identification of musical instruments using pattern recognition with cepstral coefficients as features. J Acoust. Soc Am, 1999. – 30 p.

3. Chandwadkar D.M., Sutaone M.S. Role of Features and Classifiers on Accuracy of Identification of Musical Instruments. 2nd National Conference on Computational Intelligence and Signal Processing, 2012. – Р. 66–70.

4. Davis S., Mermelstein P. Comparison of parametric representations for monosyllabic word recognition in continuously spoken sentences. IEEE Transactions on Acoustics, Speech, and Signal Processing, – 1980. – Vol. 28. – № 4. – Р. 357–366.

5. Eronen A. Comparison of features for musical instrument recognition. Workshop on Signal Processing for Audio and Acoustics, 2001. – Р. 19–22.

6. Gomez F. Robust non-linear control through neuroevolution. PhD thesis, The University of Taxes at Austin, 2003. – p. 137.

7. Nielsen A. B., Sigurdsson S., Hansen L. and Arenas-Garcia J. On the relevance of spectral features for instrument classification. Proc. Acoustics, Speech and Signal Processing, 2007. – Vol. 2. – Р. 485–488.

8. Simon O. Haykin Neural networks: a comprehensive foundation, 2d ed, Person Education, 1999. – 842 p.

9. University of Iowa Elictronic Music Studios. Music instruemnts samples. Avaliable HTTP: http://theremin.music.uiowa.edu/MIS.html, access date: 6 Jul 2014.

Человеческий мозг способен распознавать различные визуальные и звуковые образы, в том числе и отличать звучание одного музыкального инструмента от другого, даже на фоне звучания других инструментов. В данной работе рассматривается проблема распознавания звука отдельного музыкального инструмента на основе его спектральных особенностей с применением нейронных сетей.

Задача распознавания музыкальных инструментов востребована при обработке сложных музыкальных сигналов, а именно аудиозаписей музыкальных произведений различных жанров, таких как классическая музыка, эстрадная музыка и другие. Данная задача относится к классу задач Music Information Retrieval (MIR) и может быть использована для аннотирования медиаконтента, сегментации музыкальных сигналов и идентификации музыкальных объектов (нот).

Этой теме посвящено множество исследований, например [2, 3 и 7], но большинство из них используют большое количество признаков для распознавания музыкальных инструментов. Целью данной работы ставится уменьшение количества признаков с получением высокой точности при распознавании отдельно звучащих нот музыкальных инструментов.

Извлечение признаков

Музыкальный звук имеет характерную структуру в спектральном диапазоне (рис. 1.) В его составе есть основной тон, как правило, с наибольшей амплитудой, и сопутствующие гармоники – обертоны, наиболее значимыми являются первые несколько гармоник. Именно эти обертоны определяют тембр звука и соответственно музыкальный инструмент.

 Однако спектр представляет собой большой набор данных, которые нецелесообразно использовать в исходном виде для решения задачи распознавания. В связи с этим необходимо определить значимый набор признаков. В качестве такого набора было решено использовать мел-частотные кепстральные коэффициенты (MFCC). Данные коэффициенты были определены как лучшие признаки для распознавания музыкальных инструментов в работе [5]. Мел-частотные кепстральные коэффициенты представляют собой нелинейный спектр спектра, хорошо аппроксимируют слуховую систему человека, а также успешно используются для решения задач распознавания речи.

Алгоритм вычисления MFCC можно описать следующим образом [4]:

– вычисление оконного преобразования Фурье;

– нелинейное разбиение спектра на n частей c применением мел-шкалы;

– вычисление энергии сигнала для каждого интервала с применением треугольных фильтров (с перекрытием);

– вычисление логарифма энергии сигнала для каждого интервала;

– выполнение дискретного косинусного преобразования.

Для снижения сложности полученного пространства признаков мы использовали метод главных компонент (PCA). Это позволило нам уменьшить корреляцию признаков и удалить наименее значимые из них. Алгоритм вычисления главных компонент может быть описан следующим образом:

– определение матрицы корреляции;

– нахождение собственных значений и соответствующих собственных векторов;

– упорядочивание собственных векторов по соответствующим им собственным значениям (по убыванию);

– нахождение проекций входных данных на собственные векторы;

– отбрасывание последних m проекций.

Первые проекции представляют наиболее значимые компоненты в исходном векторе данных, и, соответственно, последние проекции представляют наименее значимые. Более подробное описание алгоритма может быть найдено в [8].

Классификация

Для обучения классификатора мы использовали набор маркированных примеров изолированных нот музыкальных инструментов Университета Айовы [9]. Для каждого инструмента были отобраны ноты в их эффективном рабочем диапазоне. Длительность звучания каждой ноты составляла 1–2 секунды. Мы использовали ноты, сыгранные в обычном стиле (деташе) на форте (громко), для обучения классификатора, а для тестирования – ноты, сыгранные на меццо-форте (довольно громко). Данный подход позволил приблизить процесс распознавания музыкальных инструментов к реальному сценарию.

В качестве классификатора мы использовали искусственную нейронную сеть (ИНС) прямого распространения и метод обратного распространения ошибки для обучения сети. Нейронная сеть содержала один скрытый слой. Параметры сети представлены ниже:

– число нейронов в скрытом слое: 24;

– допустимая ошибка классификации: 1 %;

– скорость обучения: 0,05;

– максимальное количество эпох обучения: 250.

Для оценки процесса обучения мы использовали кросс-валидацию. Валидационная часть составляла 30 % от обучающей выборки.

В качестве альтернативы методу обратного распространения ошибки, мы применили нейроэволюционный подход обучения сети, а именно метод Enforced Subpopulations (ESP), предложенный Фаустино Гомесом. Метод адаптирует значения весов ИНС посредством их генетической эволюции. Данный метод использует прямое кодирование и нейронную сеть прямого распространения с одним скрытым слоем. Одна из особенностей данного метода – это использование механизма взрывной мутации на основе распределения Коши для вывода процесса эволюции из локального экстремума. Кратко данный алгоритм может быть описан следующими шагами [6]:

– инициализация – создание h подпопуляций с n нейронами, где h – число нейронов в скрытом слое, n – размер популяции;

– оценка – выбирается случайная комбинация нейронов (по одному из каждой подпопуляции) и формируется нейронная сеть, затем оценивается ее приспособленность. Данная приспособленность добавляется кумулятивно к каждому нейрону этой сети. Оценка продолжается до тех пор, пока каждый нейрон не примет участие как минимум в десяти оценках;

– проверка вырождения – если приспособленность лучшей сети не улучшается в течение b поколений, то выполняется взрывная мутация. Если после двух мутаций не происходит улучшение приспособленности, то выполняется адаптация размера сети;

– рекомбинация – вычисляется средняя приспособленность каждого нейрона, затем они сортируется (в пределах подпопуляции). 25 % лучших нейронов скрещиваются с использованием одноточечного кроссинговера. Для нейронов с низкой приспособленностью выполняется мутация с распределением Коши. В конце происходит выбор лучших n нейроннов.

– этапы оценки-рекомбинации повторяются до тех пор пока не найдена сеть с требуемой приспособленностью (качеством).

Алгоритм распознавания

Алгоритм распознавания музыкальных инструментов состоит из шести блоков (рис. 2).

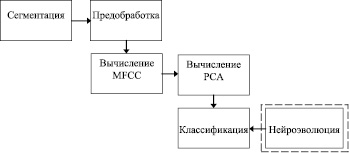
Рис. 2. Схема алгоритма распознавания

Сегментация разбивает сигнал на интервалы по 100 мс, предполагая, что спектр сигнала на этих участках постоянен в статистическом смысле. Предобработка включает увеличение амплитуды частот в верхней части спектра, а также применение оконной функции Хэминга для устранения высоких частот полученных при обрезании сигнала на границах интервала. Предобработка происходит во временнόй области сигнала. Следующими этапами являются вычисление мел-частотных кепстральных коэффициентов и применение метода главных компонент. Нейроэволюционный метод обучения ИНС является опциональным этапом алгоритма.

Полученные результаты

В результате тестирования алгоритма были найдены его оптимальные параметры. Это количество MFCC – 14 и количество главных компонент – 7. Эти параметры обеспечивают высокую точность (более 90 %) при минимизации числа используемых признаков.

Метод главных компонент позволил нам сделать входные данные более компактными, уменьшить пространство признаков (с 14 до 7) и соответственно найти наиболее оптимальную поверхность решения. На рис. 3 показаны пространства признаков MFCC (а) и PCA (б) (три первых составляющих, 3D-вид). Можно заметить, что данные располагаются более компактно и через них можно построить более простую разделяющую поверхность.

 Использование нейроэволюционного алгоритма Enforced Subpopulation не смогло дать более высокую точность в сравнении с методом обратного распространения ошибки. Результаты сравнения отражены в табл. 1.

Таблица 1

Сравнение ESP и метода обратного распространения ошибки

Точность распознавания по инструментам, полученная с помощью метода обратного распространения ошибки показана в табл. 2.

Таблица 2

Точность распознавания (по инструментам)

Средняя точность распознавания для шести музыкальных инструментов составила 92,89 %. Ошибки классификации по каждому инструменту показаны в табл. 3.

Зависимость точности распознавания от числа используемых в алгоритме музыкальных инструментов представлена на рис. 4. Инструменты добавлялись в следующем порядке: труба, фортепиано, скрипка, флейта, кларнет, маримба, тромбон, гобой, гитара, контрабас, саксофон и виолончель.

Описанный выше алгоритм был проанализирован относительно применимости к сложному сигналу. Для анализа использовалась Прелюдия Шостаковича № 5, в которой одновременно звучат два инструмента: скрипка и фортепиано. Сольные партии данных инструментов были успешно идентифицированы с помощью разработанного алгоритма. Результат анализа сложного сигнала представлен на рис. 5. Внизу вручную обозначены фактические сольные партии, выше цветом показан результат работы программы.

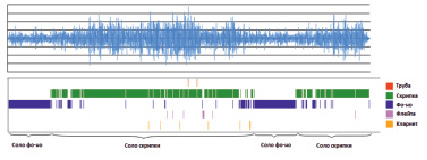
Рис. 5. Результат анализа сложного сигнала

Заключение

В данной работе мы проанализировали использование нейросетевого подхода для распознавания музыкальных инструментов на основе мел-частотных кепстральных коэффициентов. Для снижения числа признаков был использован метод главных компонент. В результате была получена высокая точность распознавания музыкальных инструментов при использовании семи признаков, подаваемых на вход классификатора на базе искусственной нейронной сети.

Исследование выполнено при частичной финансовой поддержке РФФИ в рамках научного проекта № 12-08-000296.

Ким В.Л., д.т.н., профессор, профессор ФГАОУ ВО «Национальный исследовательский Томский политехнический университет», г. Томск;

Авдеева Д.К., д.т.н., профессор, директор ООО «Медприбор», г. Томск.

Работа поступила в редакцию 05.12.2014.

Библиографическая ссылка