Следуя работе [3], определим веб-граф как граф, у которого вершинами служат веб-сайты, а ребра соединяют те вершины, между которыми имеются гиперссылки. Между двумя вершинами столько ребер, сколько есть ссылок между соответствующими сайтами, а ребра естественно считать направленными, поэтому в дальнейшем будем их называть дугами.
Под гиперссылками в данном случае мы понимаем далеко не все ссылки между сайтами. На различных страницах одного сайта могут встречаться гиперссылки на один и тот же внешний адрес, имеющие одинаковый контекст (в частном случае – анкор) и количество таких «одинаковых» гиперссылок может быть равно количеству страниц на сайте (например, ссылка на сайт вышестоящей организации). Из такого множества гиперссылок с одинаковым адресом-приёмником и контекстом, сделанных с данного сайта, в нашем исследовании мы рассматриваем только одну – ту, которая находится на странице, имеющей максимальный уровень (наивысшим считается уровень начальной страницы сайта).
Уже в конце 90-х годов ХХ века были построены первые модели для описания свойств Веба (или как часто пишут в русскоязычной литературе – Сети Интернет). В работах А.-Л. Барабаши и Р. Альберт [4–6] описан ряд важных закономерностей в поведении Веба, которые мы изложим, практически полностью цитируя работу [3].
Во-первых, веб-граф – это весьма разреженный граф. У него на n вершинах примерно k*n ребер, где k ≥ 1 – некоторая константа.
Во-вторых, диаметр веб-графа исключительно скромен. «Кликая» по ссылкам, можно с любого сайта на любой другой перейти за 5–7 нажатий клавиши компьютерной мыши. Конечно, тут есть важная оговорка. Некоторые едва появившиеся сайты могут не быть связаны с внешним по отношению к ним миром. Несколько правильнее сказать, что в веб-графе есть гигантская компонента (сильной связности) и уже ее диаметр невелик. Таким образом, веб-граф очень специфичен: будучи разреженным, он тем не менее в известном смысле тесен.
В-третьих, у веб-графа весьма характерное распределение степеней вершин. Эмпирическая вероятность того, что вершина веб-графа имеет степень d, оценивается как c/dλ, где λ ≈ 2,1, а c – нормирующий множитель, вычисляемый из условия «сумма вероятностей равна 1». Этот любопытный факт роднит Интернет с очень многими реальными сетями – биологическими, социальными, транспортными. Все они подчиняются степенному закону, только у каждой из них свой показатель λ. Последнее замечание пригодится нам несколько позже.
Развитие веб-пространства для Петрозаводского государственного университета (ПетрГУ) является одной из приоритетных задач. Теоретические и практические работы, проводимые в рамках этой задачи, позволили сформировать большую базу данных, содержащую, в частности, информацию о веб-графе информационного веб-пространства ПетрГУ. В статье приводятся некоторые результаты, представляющие собой ответ на вопрос: насколько веб-граф ПетрГУ, построенный на основе данных, собранных в 2014 году, является веб-графом Барабаши-Альберт (Barabasi-Albert model), в чём его основные отличия и особенности, и каковы тенденции его развития в будущем в случае использования целенаправленных административных воздействий на него посредством гиперссылок.
Веб-граф ПетрГУ
Общее количество сайтов, составляющих веб-пространство ПетрГУ, в данном исследовании равно 147. Перечислим некоторых наиболее характерных представителей веб-пространства ПетрГУ:
– официальный сайт университета (petrsu.ru);
– сайты факультетов, кафедр, научной библиотеки, ботанического сада, институтов, центров, филиалов университета, университетских лицеев (математический факультет – mf.petrsu.ru);
– сайты издательств, научных журналов, медиа-ресурсов (журнал «Принципы экологии» – ecopri.ru);
– сайты структурных подразделений университета, не вошедшие в группы 2–6 (Региональный центр новых информационных технологий, rcnit.petrsu.ru);
– сайты научных конференций, программ и проектов, организуемых и выполняемых университетом (конференция «Космос братьев Гримм» – grimms.petrsu.ru);
– сайты учебных ресурсов, информационно-справочных систем и ресурсов университета («Аспирантура ПетрГУ» – aspirant.petrsu.ru);
– персональные сайты сотрудников университета (сайт Андрея Мезенцева – amez.petrsu.ru);
– другие сайты: сайты творческих организаций, профкома (Туристический клуб ПетрГУ «Сампо» – sampo-club.ru).
Сканирование сайтов веб-пространства ПетрГУ с целью сбора исходящих гиперссылок производилось программой BeeCrawler [8]. Для хранения, обработки и анализа гиперссылок использовалась специализированная база данных внешних гиперссылок [1]. На 147 сайтах веб-пространства ПетрГУ было отсканировано около 100 000 страниц и сформировано множество, содержащее 11 200 исходящих с этих сайтов гиперссылок. Далее из 11 200 гиперссылок были отобраны 1352 гиперссылки, которые связывают сайты веб-пространства ПетрГУ, и построен веб-граф G = G(V,E); здесь V (vertex) – множество вершин, соответствующих сайтам веб-пространства, E (edge) – множество дуг, соответствующих гиперссылкам, связывающим эти сайты, |V| = n = 147, |E| = m = 1352. Поскольку ряд сайтов связан гиперссылками в количестве, большем, чем 1, то мы имеем G(V,E) как ориентированный граф с кратными дугами без петель.
На рис. 1 приводится несколько упрощённое изображение веб-графа G(V,E): во избежание загромождения рисунка кратные дуги не нарисованы, приведены названия только некоторых вершин и исключены изолированные вершины. Головной сайт petrsu.ru представлен вершиной с наибольшей степенью, расположенной почти в самом центре рисунка.

Рис. 1. Веб-граф ПетрГУ
Девять изолированных вершин соответствуют сайтам, которые не связаны гиперссылками с другими сайтами ПетрГУ, и 40 вершин являются «висячими», то есть имеют либо только исходящие, либо только входящие дуги.
Свойства веб-графа ПетрГУ
Для веб-графа ПетрГУ свойство разреженности графа очевидно. При n = 147 вершин мы имеем m = 1352, т.е. k = 9,2. Тогда как в максимальном случае полного графа (даже без кратных дуг) их должно быть 21462, т.е. k потенциально может увеличиться еще в 15 раз, а с учётом средней кратности дуг, равной 3,2, веб-граф наполнен дугами примерно на 1/50. Если взять веб-граф ПетрГУ без кратных дуг, то количество дуг оказывается равным 419, то есть свойство разреженности графа становится ещё более очевидным.
Компонента сильной связности (КСС) веб-графа ПетрГУ достаточно велика, она содержит 89 вершин, и её диаметр равен 5. Отметим, что потенциально компонента сильной связности имеет все предпосылки к росту, поскольку, если рассмотреть этот же веб-граф, но с неориентированными дугами, то его компонента связности содержит уже 138 вершин (более 90 % всех сайтов) и её диаметр равен 4.
Таким образом, для веб-графа ПетрГУ мы имеем практически полное выполнение первых двух свойств, характерных для модели Барабаши-Альберт: разреженный граф с КСС диаметром 5. Более того, можно считать, что в виде КСС мы имеем аналог т.н. «гигантской компоненты» для графа с небольшим количеством вершин.
Более сложно обстоит дело с распределением степеней вершин. Например, вряд ли можно было изначально предположить, что в веб-графе ПетрГУ мы получим коэффициент λ = 2,1. Как сказано в работе [3], Барабаши и Альберт «... предложили очень разумный взгляд на процесс формирования интернета. Давайте считать, сказали они, что в каждый момент времени появляется новый сайт, и этот сайт ставит фиксированное количество ссылок на своих предшественников. На кого он предпочтет сослаться? Наверное, на тех, кто и так уже популярен. Можно допустить, что вероятность, с которой новый сайт поставит ссылку на один из прежних сайтов, пропорциональна числу уже имевшихся на тот сайт ссылок. Модели случайных графов, основанные на описанной идее, называются моделями предпочтительного присоединения. В своих работах Барабаши и Альберт никак не конкретизировали, какую именно из этих моделей они предлагают рассматривать. А эти модели исключительно разнородны по своим свойствам».
В случае веб-графа ПетрГУ, как уже сказано выше, наибольшую степень (суммарное количество входящих и исходящих дуг) d = 699 имеет вершина, соответствующая официальному сайту petrsu.ru. Следующим со значением d = 148 является сайт Карельской государственной педагогической академии, вошедшей более года назад в состав ПетрГУ; на третьем месте со значением d = 107 находится сайт «Электронная библиотека Республики Карелия» elibrary.karelia.ru.
Графики функций вероятности распределения степеней вершин в веб-графе ПетрГУ приводятся на рис. 2. По оси абсцисс указывается значение d, а по оси ординат – значение вероятности того, что вершина веб-графа имеет степень d. Ломаной линией изображена функция, построенная на имеющихся эмпирических значениях, а непрерывной – функция тренда для эмпирической функции.
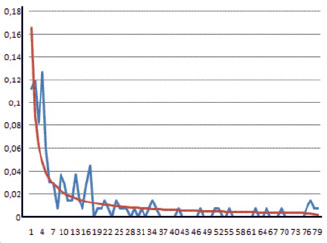
Рис. 2. Распределение степеней вершин веб-графа ПетрГУ
Построенная по эмпирическим данным функция тренда имеет вид: p(d) = P[X = d] = 6,046/d0.9, здесь X – дискретная случайная величина (степень вершины, натуральное число), p(d) – вероятность того, что она принимает значение d, нормирующий коэффициент с = 6,046 и l = 0,9.
Заметим, что по сравнению с моделью Барабаши-Альберт для веб-графа ПетрГУ мы имеем значительно меньшие значения вероятностей для малых значений d. Если применительно к веб-графу ПетрГУ взять l = 2,1 (как в модели Барабаши-Альберт), то получим первые три значения P[X = 1] = 0,65, а P[X = 2] = 0,15, P[d = 3] = 0,06, а в случае функции тренда при l = 0,9 – P[d = 1] = 0,17, P[d = 2] = 0,09, P[d = 3] = 0,06. Можно предположить, что в относительно небольшом множестве сайтов, составляющих веб-пространство вуза, работает ссылочный механизм, который значительно уменьшает вероятность появления и длительного сохранения «висячих» вершин (только для них Х = 1), поскольку сайты образуют так называемое тематическое сообщество, свойства которого ранее были описаны в работе [2].
Тематическое веб-пространство крупных организаций характеризуется наличием головного сайта (официального сайта организации или, возможно, единого портала, некоей «точки входа»), а остальные сайты составляют «сопутствующее множество» [2]. Естественно, что головной сайт будет иметь очень большое количество входящих и исходящих ссылок с сайтов сопутствующего множества, поэтому степень d головного сайта имеет оценку снизу 2*(n-1). В нашем случае для официального сайта ПетрГУ petrsu.ru значение функции тренда (P[d = 699] = 0,00046) очень мало, но объяснимо. И это объяснение кроется не только в предыдущем высказывании. Для графов тематических сообществ в ряде случаев отмечается очень большое количество кратных гиперссылок, связывающих отдельные сайты. Например, в нашем случае сайт petrsu.ru имеет 63 гиперссылки на упоминавшийся ранее сайт elibrary.karelia.ru, а сайт Регионального центра по трудоустройству (созданного при управлении по социальной и воспитательной работе ПетрГУ) job.petrsu.ru имеет 63 ссылки на petrsu.ru.
В первом случае это в основном ссылки на учебники и учебные пособия, сделанные со страниц кафедр, не имеющих собственных сайтов и поэтому размещающих учебную информацию на официальном сайте, а во втором – полезные ссылки как для выпускников, так и для организаций, заинтересованных в подготовленных кадрах.
Заключение
Несмотря на небольшие размеры веб-графа ПетрГУ (в масштабах всего Веба), можно сказать, что в целом он имеет те же свойства, которые присущи модели Барабаши-Альберт, предложенной 15 лет назад, когда Веб только зарождался. Отсюда можно сделать основной вывод о том, что прямые административные воздействия (типа предписаний по созданию ссылок, связывающих сайты ПетрГУ) ранее не предпринимались.
Более «плавное» поведение вероятности распределения вершин в графе легко объясняется «знаниями» разработчиков сайтов о других сайтах ПетрГУ. Отсюда также следует достаточно большой размер КСС, малое количество изолированных сайтов и тот факт, что компонента связности (для неориентированного графа) содержит все неизолированные вершины.
Наличие безусловного лидера по количеству гиперссылок также является неотъемлемой особенностью тематического сообщества сайтов, имеющих отношение к одной организации.
Вместе с тем, если исходить из того, что веб-пространство организации (в нашем случае – ПетрГУ) имеет тенденцию к наращиванию своего присутствия в Вебе, то, по-видимому, естественное возникновение новых гиперссылок в веб-пространстве является достаточно долгим путём. Результаты проведенного исследования показывают, что ускорение этого процесса возможно за счёт использования административных воздействий, напрямую обязывающих создателей сайтов, входящих в веб-пространство ПетрГУ, усилить ссылочную активность «внутри» университетского сообщества. При этом следует помнить, что такое усиление ссылочной активности должно представлять собой отражение естественных связей, но, ни в коем случае не переход к спам-сообществу [7], а значит должно тщательно планироваться и отслеживаться.
Работа выполнена при поддержке Программы стратегического развития Петрозаводского государственного университета на 2012–2016 годы.
Рецензенты:Гридина Е.Г., д.т.н., профессор, директор Информационно-вычислительного центра Национального исследовательского университета «МЭИ», г. Москва;
Кузнецов В.А., д.т.н., профессор, профессор кафедры прикладной математики и кибернетики Петрозаводского государственного университета, г. Петрозаводск.
Работа поступила в редакцию 05.12.2014.
Библиографическая ссылка
Марахтанов А.Г., Насадкина О.Ю., Печников А.А. О МОДЕЛИ БАРАБАШИ-АЛЬБЕРТ ПРИМЕНИТЕЛЬНО К ВЕБ-ГРАФУ ПЕТРОЗАВОДСКОГО ГОСУДАРСТВЕННОГО УНИВЕРСИТЕТА // Фундаментальные исследования. 2014. № 12-1. С. 33-37;URL: https://fundamental-research.ru/ru/article/view?id=36067 (дата обращения: 28.02.2026).



