Одной из основных задач современной образовательной политики является обеспечение качества образования, сохранения его фундаментальности, соответствия перспективным потребностям личности, общества, государства. В условиях штатного проведения единого государственного экзамена появилась возможность осуществления мониторинга качества освоения образовательных программ отдельных дисциплин, в частности математики. Опыт Алтайской краевой предметной комиссии ЕГЭ по математике показывает возможности в выявлении погрешностей участников экзамена, проектировании предупреждающих и корректирующих мероприятий на основе анализа результатов ЕГЭ.
Исследования проблем образовательного процесса показывают важность того, что «педагогов следует обучать наблюдению, диагностике посредством вопросов и формальному оцениванию, разработке учебной программы, образцов учебных достижений и различным способам вмешательства в процесс обучения» [1, с. 12].
Показателями, по которым учитель имеет возможность судить о знаниях и умениях учащегося, служат погрешности, допущенные учащимися при работе со средствами контроля, предложенными учителем [2, с. 152–163]. Наряду с погрешностями, показателями, по которым учитель может судить о знаниях и умениях учащихся, могут быть такие, как:
– изложение изученного материала грамотным языком в определенной логической последовательности;
– обращение к иллюстрации теоретических положений конкретными примерами, правильное применение теории в новой для ученика ситуации;
– использование в процессе решения различных форм представления содержания математических фактов (вербальная, графическая, знаково-символическая);
– самостоятельность в процессе выполнения задания и др.
Выявление погрешностей учащихся преследует цель не только осуществления контроля, но совершенствования учебного процесса, поскольку позволяет наметить пути преодоления типичных ошибок и недочётов учащихся в дальнейшем обучении. Функции анализа ошибок достаточно давно выделены в научно-методической литературе. «Рассмотреть с учащимися средней школы хотя бы некоторые такие ошибки полезно по двум причинам: во-первых, хорошо ознакомившись с какой-нибудь ошибкой, мы страхуем себя от повторения такой ошибки в будущем; во-вторых, самый процесс разыскания ошибки легко сделать увлекательным для учащихся, и изучение ошибок становится средством поднять интерес к изучению математики» [3, с. 3].
Недостатком единого государственного экзамена является то, что полная картина его результатов оказывается скрыта от учителя. Но для совершенствования практики обучения, повышения его качества следует выполнять детальный анализ работ учащихся, выявляя как сильные стороны при решении задач контрольно-измерительных материалов (КИМ), так и погрешности учащихся. Ошибки, допускаемые учащимися при решении задач, условно разделим на две группы: индивидуальные и типовые. Вскрывать индивидуальные ошибки участников единого государственного экзамена и осуществлять деятельность по их искоренению может учитель на основании анализа работ учащихся своего класса. Для выявления типичных ошибок целесообразно осуществлять анализ работ на более обширной совокупности работ учащихся, возможно даже на генеральной совокупности. Такой анализ может осуществляться региональными и федеральными предметными комиссиями. Его результаты могут стать предметом обсуждения на методических объединениях различного уровня.
Содержание и структура экзаменационной работы ЕГЭ по математике дают возможность достаточно полно проверить комплекс умений по предмету:
● уметь использовать приобретенные знания и умения в практической деятельности и повседневной жизни;
● уметь выполнять вычисления и преобразования;
● уметь решать уравнения и неравенства;
● уметь выполнять действия с функциями;
● уметь выполнять действия с геометрическими фигурами, координатами и векторами;
● уметь строить и исследовать математические модели.
Общие результаты выполнения заданий экзаменационной работы наглядно демонстрирует рисунок.
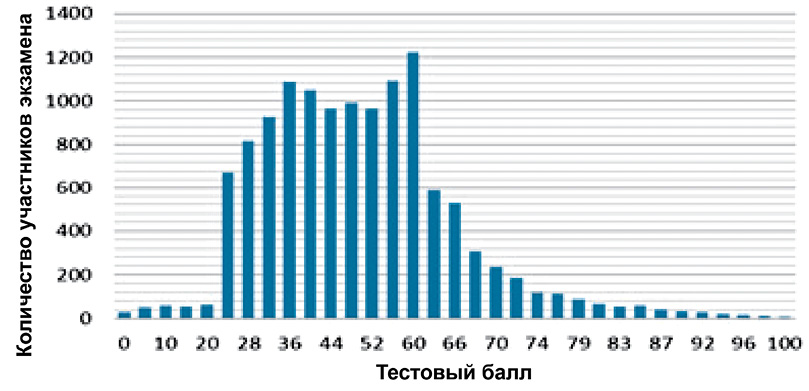
Распределение числа участников по полученным тестовым баллам (ЕГЭ по математике, Алтайский край, 2013 г.)
Комплексный анализ результатов образования, включая анализ результатов ЕГЭ последних лет, показывает, что в преподавании математики в нашей стране накопился ряд проблем, решение которых позволит повысить качество образования. Условно эти проблемы можно разделить на группы:
– мотивационные: общественная недооценка значимости математического образования; перегруженность школьной математики техническими элементами; отсутствие ответственности учащихся за результаты своего образования и др.
– избыточное единство требований к результатам образования: единые требования к результатам обучения нереалистичны для значительной части учащихся; учитель не в состоянии удовлетворить принципиально разные запросы, руководствуясь общим для всех образовательным стандартом и программами и др.;
– содержательные проблемы и неэффективность: отсутствие связи обучения с потребностями государства и общества в будущих специалистах и специфических математических знаниях и методах; математика преподается формально и др. [4].
Анализ результатов выполнения заданий части В позволяет сделать ряд следующих выводов.
1. Положительным результатом экзамена традиционно является овладение значительной частью (96,17 % – при решении задачи В2) выпускников школ базовыми умениями использовать приобретённые знания из курса алгебры и начал математического анализа в практической деятельности и повседневной жизни, что несколько превышает планируемые показатели.
2. Показатели выше среднего (в пределах нормы) учащиеся продемонстрировали при выполнении на базовом уровне действий с геометрическими фигурами (в частности, при нахождении площади параллелограмма – 85,71 % – задача В3; нахождении угла в треугольнике – 84,25 % – задача В6), при решении простейших логарифмических уравнений (82,94 % – задача В5), при выяснении вероятности случайного события (80,52 % – задача В10).
3. В пределах нормы показатели умения вычислять значение тригонометрического выражения с использованием формул приведения (70 % – задача В7), преобразовывать выражения, включающие арифметические операции (76,07 % – задача В4).
4. Показателей ниже нормы умений, проверяемых базовой частью, в 2013 году нет. Находившиеся ниже нормы в 2012 году показатели усвоения умения вычисления объемов многогранников и тел вращения повысились с 29,00 % до 50,93 % (задача В11). Показатели усвоения умения применять производную к исследованию функции повысились с 34,48 до 58,64 % (задача В14); показатели усвоения умения строить и исследовать простейшие математические модели (сюжетная задача В13) повысились с 38,20 до 56,59 %; показатели усвоения умения использовать при решении задач геометрический смысл производной повысились с 45,60 до 53,25 % (задача В8).
5. О некоторых проблемах качества математической подготовки учащихся свидетельствуют результаты, полученные при решении задач, нацеленных на проверку умений:
● выполнять действия с геометрическими фигурами, координатами и векторами (проверяемое при решении задачи на нахождение объёма), к примеру, 15 % участников экзамена при решении задачи B11 неверно указали в качестве ответа число 30, по-видимому, остановившись в ходе решения на вычислении объёма заданной призмы, не искомой пирамиды;
● выполнять действия с функциями (проверяемое при решении задач на использование геометрического смысла производной при решении задач), к примеру, более 5 % участников экзамена не решали задачу B8;
● строить и исследовать простейшие математические модели (проверяемое на содержании сюжетной задачи, приводящей к составлению и решению уравнения);
● применять математические методы для решения содержательных задач из различных областей науки и практики;
● применять производную к нахождению наибольшего (или наименьшего) значения функции, заданной на отрезке, к примеру, задачу В14 не решало более 16 % участников экзамена.
Анализ веера ответов, предложенных участниками экзамена, показывает наличие определённых проблем при решении отдельных задач (в частности, В1, B4, B5, B8, B12, B13), поскольку наличие большого количества вариантов ответов может свидетельствовать, в частности, о неустойчивости понимания учащимися соответствующего учебного материала. Проявляется статистическая зависимость между рядом количества вариантов ответов на задачи типа В и рядом количества не приступавших к решению таких задач (коэффициент корреляции между этими данными равен 0,42).
Анализ результатов решения задач с развёрнутым ответом позволил выявить следующие факты.
1. Результат выполнения задания С1 свидетельствует о сформированности чем у больше четверти участников экзамена (25,39 % при ожидаемых 10–50 %) определённых умений решать тригонометрические уравнения и отбирать корни уравнения, принадлежащие наперёд заданному промежутку. Однако, отмечается снижение результата решения задания С1 по сравнению с 2012 годом, когда положительные баллы получили 32,4 % от участвовавших в экзамене.
2. По сравнению с 2012 годом существенно улучшились показатели освоения умений выполнять действия с геометрическими фигурами, координатами и векторами при решении стереометрической задачи С2. Находящийся в 2012 году ниже нормы процент решивших задачу С2 на нахождение расстояния от точки до плоскости (3,1 %), в 2013 году увеличился, и задачу на вычисление площади сечения многогранника плоскостью решили 15,01 %; что соответствует норме (10–50 %).
3. Незначительно ниже нормы оказался показатель освоения умений выполнять действия с геометрическими фигурами, координатами и векторами при решении планиметрической задачи С4 о рассмотрении двух конфигураций касающихся окружностей. Он увеличился по сравнению с 2012 годом с 3,73 до 9,84 % и стал близким к норме (10–50 %).
4. Результаты освоения разделов части С свидетельствуют об улучшении в 2013 году по сравнению с 2012 годом качества обучения геометрии в школах Алтайского края.
Анализ работ 2013 года позволил констатировать несколько положительных результатов ЕГЭ по математике.
1. Показателей ниже нормы умений, проверяемых базовой частью, в 2013 году нет, чего не наблюдалось в последние годы. Это свидетельствует о повышении уровня результатов математического образования в Алтайском крае.
2. Овладение значительной частью выпускников школ на уровне выше нормы базовыми умениями использовать приобретённые знания из курса алгебры и начал математического анализа в практической деятельности и повседневной жизни, умением решать простейшую задачу на нахождение площадей треугольника, параллелограмма, трапеции, углов в треугольнике, а также умением решать логарифмические уравнения и находить вероятность случайного события, что проявилось при решении задач первой части экзамена.
3. При решении задач второй части положительная тенденция состоит в уверенном владении учащимися многими способами отбора корней тригонометрического уравнения из указанного промежутка при решении задачи типа С1: с помощью единичной окружности, с помощью графика тригонометрической функции, с помощью числовой прямой, решая двойное линейное неравенство. Немало учащихся демонстрируют полное владение одним из наиболее рациональных (на их взгляд) способов.
4. Значительно улучшились показатели освоения умений выполнять действия с геометрическими фигурами, координатами и векторами при решении стереометрической задачи С2. Несмотря на то, что активно использованные в прошлом году векторный, координатно-векторный, координатный методы явно не являлись удачными в стереометрической задаче на нахождение площади сечения многогранника, учащиеся сумели актуализировать необходимые знания в новой ситуации.
5. Большее разнообразие способов решения задачи с параметром С5 (функциональный, функционально-графический, аналитический) среди работ участников экзамена позволяет сделать вывод о продвинутом уровне готовности к экзамену многих учащихся, далеко выходящей за рамки базовой подготовки.
6. С заданиями базового уровня справились 72,51 % участников экзамена, что свидетельствует о положительной тенденции отработки обязательных результатов обучения математике.
Однако предметная комиссия по математике, проанализировав результаты, выявила ряд недочетов в математической подготовке выпускников школы, отдельные из которых отмечались и в прошлые годы:
● непонимание, неосознание сути понятия «равносильность преобразования» при решении уравнений или неравенств и, соответственно, допущение в процессе решения неравносильных преобразований (в частности, деление обеих частей уравнения на выражение с переменной без исследования возможности его равенства нулю при некотором значении переменной);
● несформированность четкого алгоритма решения задачи с параметром, что приводит к потерям решений. В результате учащиеся приводят неполное или незавершенное решение задачи с параметром С5, рассмотрев не все случаи раскрытия модуля, исследовав не все случаи значений новой введенной переменной или параметра, не проведя проверки найденных значений параметра;
● формализм в построении идеи решения задачи, «узкий взгляд» на условие задачи, учет не всех нюансов задания: в частности, например, условие, что «уравнение должно иметь единственное решение» в задаче С5 акцентирует все внимание учащихся, оставляя без учета другие компоненты условия (присутствие модуля, симметричность корней и т.д.);
● недостаточная сформированность умений учащихся применять методы решения системы различных видов неравенств, неглубокое владение понятием логарифма, незнание свойств логарифмической и показательной функций. При решении логарифмических и показательных неравенств зачастую решение неравенства подменяется решением уравнения, т.е. отсутствует шаг с использованием метода интервалов или кривой знаков. Также затруднения учащихся связаны с обратной заменой при решении показательного или логарифмического неравенства с помощью метода введения новой переменной;
● с заданиями повышенного уровня справилось 10,6 % участников экзамена в Алтайском крае, а с заданиями высокого уровня – 2,16 %. Причём в отдельных муниципальных образованиях с заданиями высокого уровня не справился ни один участник экзамена.
Результаты единого государственного экзамена наглядно показывают проблемы в обеспечении качества обучения математике в регионе. Одним из аспектов решения обозначенных проблем видится проектирование предупреждающих и корректирующих действий по преодолению погрешностей в предметных результатах ЕГЭ по математике. Процессный подход к обучению ориентирует на чёткую идентификацию таких действий, как взаимосвязанных и взаимодействующих между собой, т.е. реализуемых как процесс. Выявление погрешностей учащихся преследует цель не только осуществления контроля, но совершенствования учебного процесса, поскольку позволяет наметить пути преодоления типичных ошибок и недочётов учащихся в дальнейшем обучении.
Современные средства оценивания результатов обучения в практике применения ориентированы на оценивание достижений учащихся в ущерб выявлению погрешностей. Это проявляется и в генезисе критериев оценивания экзаменационных работ (из текстов которых «уходит» термин), в недостаточности содержательного анализа предметных результатов (при констатации фактов недостаточных результатов при решении определённых задач зачастую не вскрываются погрешности в предметной подготовке и пути их предупреждения). В связи с этим возникают противоречия, связанные с применением современных средств на различных уровнях образования, доверием к ним всех заинтересованных сторон.
Анализируя содержание задач второй части ЕГЭ, П.И. Самсонов отмечает: «Современному учителю пришли на помощь современные технологии – теперь он может увидеть сканы работ своих учеников, а значит, может анализировать содержательную составляющую результатов экзамена. И здесь очень важно выйти на опережение ситуации – на предупреждение возможных ошибок, а это – и иной подбор заданий и упражнений для учебной работы ученика на уроке и дома, и иное поурочное планирование, и иная подготовка учителя к урокам» [5; c. 14].
Рецензенты:Брейтигам Э.К., д.п.н., профессор ка федры алгебры и методики обучения математике, ФГБОУ ВПО «Алтайская государственная педагогическая академия», г. Барнаул;
Овчаров А.В., д.п.н., профессор, директор института физико-математического образования, ФГБОУ ВПО «Алтайская государственная педагогическая академия», г. Барнаул.
Работа поступила в редакцию 28.11.2014.
Библиографическая ссылка
Кисельников И.В. АНАЛИЗ РЕЗУЛЬТАТОВ ЕГЭ ПО МАТЕМАТИКЕ В АЛТАЙСКОМ КРАЕ В СИСТЕМЕ ОБЕСПЕЧЕНИЯ КАЧЕСТВА ОБУЧЕНИЯ МАТЕМАТИКЕ // Фундаментальные исследования. 2014. № 11-11. С. 2510-2514;URL: https://fundamental-research.ru/ru/article/view?id=35976 (дата обращения: 27.02.2026).



