Волны напряжений различной природы, распространяясь в деформируемом теле, взаимодействуют друг с другом. После трехкратного или четырехкратного прохождения и отражения волн напряжений в теле процесс распространения возмущений становится установившимся, напряжения и деформации усредняются, тело находится в колебательном движении. Некоторые результаты рассматриваемого численного метода приведены в следующих работах [1–2, 4–10].
Моделирование широко применяется при решении научных и прикладных задач. Математические модели являются наиболее характерными в естественнонаучных исследованиях. Физические модели имитируют часть свойств исследуемого объекта. Поставленная задача реализуется с помощью уравнений математической нестационарной динамической теории упругости. При решении сложных задач возникают проблемы оценки достоверности полученных результатов. На основании изложенного можно утверждать, что оценка точности и достоверности результатов численного моделирования волн напряжений в областях сложной формы является актуальной фундаментальной и прикладной научной задачей. В работах [1–2, 4–5, 9–10] приведена информация о постановке волновых задач теории упругости.
Точные уравнения двумерной (плоское напряженное состояние) динамической теории упругости имеют вид
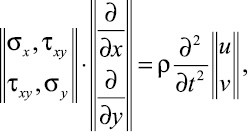 (x, y) ∈ Γ;
(x, y) ∈ Γ;
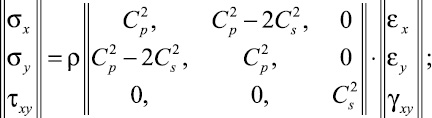
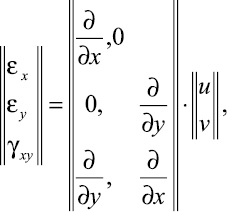 (x, y) ∈ (Γ ∪ S), (1)
(x, y) ∈ (Γ ∪ S), (1)
где σx, σy и τxy – компоненты тензора упругих напряжений; εx, εy и γxy – компоненты тензора упругих деформаций; u и v – составляющие вектора упругих перемещений вдоль осей OX и ОУ соответственно; ρ – плотность материала; 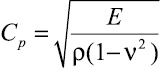 – скорость продольной упругой волны;
– скорость продольной упругой волны; 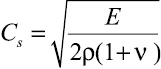 – скорость поперечной упругой волны; ν – коэффициент Пуассона; E – модуль упругости; S (S1 ∪ S2) – граничный контур тела Γ.
– скорость поперечной упругой волны; ν – коэффициент Пуассона; E – модуль упругости; S (S1 ∪ S2) – граничный контур тела Γ.
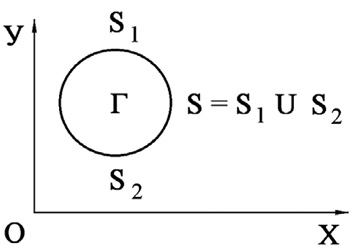
Рис. 1. Некоторое тело Г в прямоугольной декартовой системе координат XOY
Систему (1) в области, занимаемой телом Γ, следует интегрировать при начальных и граничных условиях. Начальные условия в области Γ зададим в виде
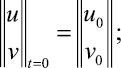
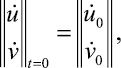 (x, y) ∈ Γ, (2)
(x, y) ∈ Γ, (2)
где u0, v0, 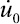 и
и 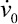 – заданные в области Γ функции.
– заданные в области Γ функции.
Граничные условия зададим в виде:
составляющих компонентов тензора упругих напряжений на границе S1
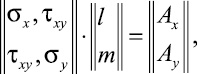 (x, y) ∈ S1; (3)
(x, y) ∈ S1; (3)
составляющих компонентов вектора упругих перемещений на границе S2
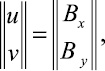 (x, y) ∈ S2, (4)
(x, y) ∈ S2, (4)
где 1 и m – направляющие косинусы; Ax, Ay, Bx и By – заданные на границе S функции.
Для решения двумерной плоской динамической задачи теории упругости с начальными и граничными условиями используем метод конечных элементов в перемещениях. Задача решается методом сквозного счета, без выделения разрывов. Чтобы выполнить динамический расчет методом конечных элементов, нужно иметь матрицу жесткости и матрицу инерции конечного элемента.
Принимая во внимание определение матрицы жесткости, вектора инерции и вектора внешних сил для тела Γ, записываем приближенное значение уравнения движения в теории упругости:
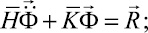
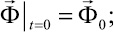
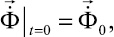 (5)
(5)
где 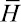 – матрица инерции;
– матрица инерции; 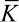 – матрица жесткости;
– матрица жесткости; 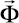 – вектор узловых упругих перемещений;
– вектор узловых упругих перемещений; 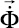 – вектор узловых упругих скоростей перемещений;
– вектор узловых упругих скоростей перемещений; 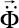 – вектор узловых упругих ускорений;
– вектор узловых упругих ускорений; 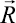 – вектор узловых упругих внешних сил.
– вектор узловых упругих внешних сил.
Соотношение (5) – система линейных обыкновенных дифференциальных уравнений второго порядка в перемещениях с начальными условиями. Таким образом, с помощью метода конечных элементов в перемещениях, линейную задачу с начальными и граничными условиями привели к линейной задаче Коши (5). В работах [1–10] приведена информация о численном моделировании нестационарных волн напряжений в деформируемых телах.
Для интегрирования уравнения (5) конечноэлементным вариантом метода Галеркина приведем его к следующему виду:
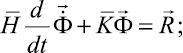
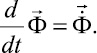 (6)
(6)
Интегрируя по временной координате соотношение (6) с помощью конечноэлементного варианта метода Галеркина, получим двумерную явную двухслойную конечноэлементную линейную схему в перемещениях для внутренних и граничных узловых точек:
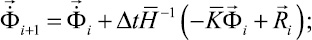
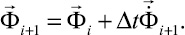 (7)
(7)
Основные соотношения метода конечных элементов в перемещениях получены с помощью принципа возможных перемещений и конечноэлементного варианта метода Галеркина. Система уравнений (5) для внутренних и граничных узловых точек, полученная в результате интегрирования уравнения движения теории упругости, должна давать решение, сходящееся к решению исходной системы (1). Шаг по временной переменной Δt определяем из следующего соотношения:
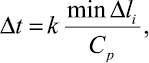 (i = 1, 2, 3, ..., r), (8)
(i = 1, 2, 3, ..., r), (8)
где Δl – длина стороны конечного элемента.
Результаты численного эксперимента показали, что при k = 0,5 обеспечивается устойчивость двумерной явной двухслойной конечноэлементной линейной схемы в перемещениях для внутренних и граничных узловых точек на квазире гулярных сетках.
На основе метода конечных элементов в перемещениях разработаны алгоритм и комплекс программ для решения линейных плоских двумерных задач, которые позволяют решать сложные задачи при взрывных воздействиях на уникальные сооружения. При разработке комплекса программ использовался алгоритмический язык Фортран-90. Исследуемая область разбивается по пространственным переменным на треугольные конечные элементы с тремя узловыми точками с линейной аппроксимацией упругих перемещений и на прямоугольные конечные элементы с четырьмя узловыми точками с билинейной аппроксимацией упругих перемещений. По временной переменной исследуемая область разбивается на линейный конечный элемент первого порядка. Некоторые вопросы в области постановки, разработки методики, алгоритма и результатов решенных нестационарных динамических задач рассмотрены в следующих работах [1–10]. Рассмотрим задачу об отражении упругих волн напряжений в виде треугольного импульса от свободной поверхности.
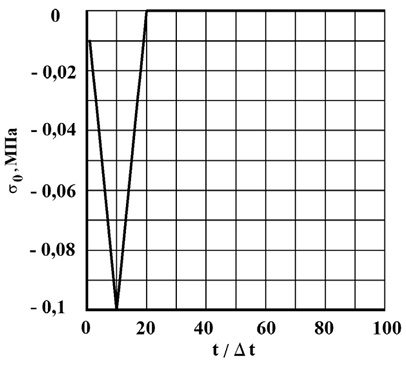
Рис. 2. Воздействие в виде треугольного импульса
На границе пластинки AB (рис. 3) приложено нормальное напряжение σy (рис. 2), которое при 0 ≤ n ≤ 10 (n = t/Δt) изменяется линейно от 0 до P, а при n ≥ 10 от P до 0 (P = σ0, σ0 = –0,1 МПа (–1 кгс/см2)). Граничные условия для контуров BC и AD при t > 0 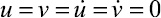 . Контур CD свободен от нагрузок. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных.
. Контур CD свободен от нагрузок. Отраженные волны от контуров BC и AD не доходят до исследуемых точек при 0 ≤ n ≤ 190. Исследуемая расчетная область имеет 4221 узловую точку и 4000 конечных элементов. Решается система уравнений из 16884 неизвестных.
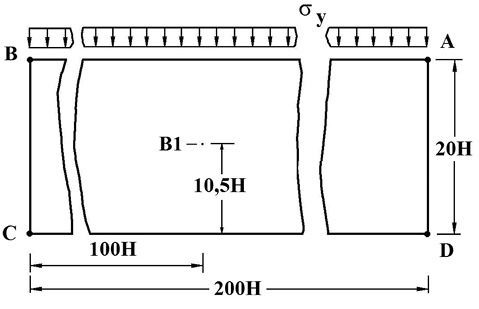
Рис. 3. Постановка задачи об отражении волн напряжений
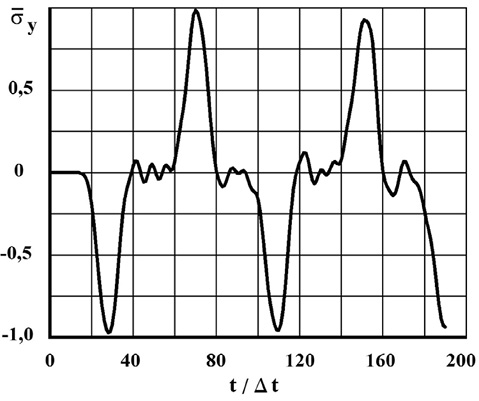
Рис. 4. Изменение упругого нормального напряжения 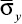 во времени n в точке B1
во времени n в точке B1
Для примера на рис. 4 представлено изменение нормального напряжения 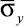
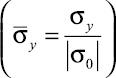 во времени n в точке B1. При отражении от свободной поверхности пластинки волна сжатия становится волной растяжения, которая может привести к отколу.
во времени n в точке B1. При отражении от свободной поверхности пластинки волна сжатия становится волной растяжения, которая может привести к отколу.
Достоверность рассматриваемого численного метода приведена в работах [2, 4–10]. Сравнение с результатами других методов показало хорошее совпадение, что позволяет сделать вывод о физической и математической достоверности результатов численного решения динамических задач, полученных методом конечных элементов в перемещениях.
Рецензенты:Савчин В.М., д.ф.-м.н., профессор кафедры математического анализа и теории функций факультета физико-математических и естественных наук, Российский университет дружбы народов, г. Москва;
Зволинский В.П., д.х.н., профессор кафедры экологического мониторинга и прогнозирования экологического факультета, Российский университет дружбы народов, г. Москва.
Работа поступила в редакцию 28.11.2014.
Библиографическая ссылка
Мусаев В.К., Ситник С.В., Тарасенко А.А., Ситник В.Г., Зюбина М.В. МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ОТРАЖЕНИЯ НЕСТАЦИОНАРНЫХ УПРУГИХ ВОЛН НАПРЯЖЕНИЙ В ВИДЕ ТРЕУГОЛЬНОГО ИМПУЛЬСА ОТ СВОБОДНОЙ ПОВЕРХНОСТИ ПЛАСТИНКИ // Фундаментальные исследования. 2014. № 11-11. С. 2375-2379;URL: https://fundamental-research.ru/ru/article/view?id=35949 (дата обращения: 15.01.2026).



