Задача оптимизации треугольной геометрической сети на сфере по критерию минимума типоразмеров элементов уже ставилась многими авторами различных систем сферической разрезки [1–2]. Во всех случаях решений находилась одна или несколько схем разрезок сферы с использованием в основном осей симметрии в виде главных линий (линий больших окружностей сферы), линий параллельных сечений сферы, а также совместимости частей граней правильных многогранников. Очевидно, что размещение на сфере правильных и неправильных шестиугольников, вписанных в окружности, т.е. фигур плоских или составленных в свою очередь из сферических треугольников (рис. 1 а, б) с минимальными размерами ребер, имеет оптимальное решение в виде сети, образованной на основе окружностей минимальных радиусов, т.е. окружностей на сфере, полученных при касании трех смежных окружностей, центры которых находятся на наименьшем расстоянии друг от друга [2–5]. Данное направление активно развивается рядом зарубежных ученых, а в России новосибирской школой [1].
Сферический шестиугольник можно представить как два четырехугольника с заданными сторонами, и он имеет максимальную площадь тогда, когда вписан в окружность. Шестиугольные панели, вписанные в окружности с минимальными радиусами (т.е. касающиеся), будут иметь минимальные размеры и максимальные площади при заданном числе граней треугольной сети сферы. Т.е. элементы сети в виде радиусов будут иметь минимальную длину, так как представляют собой кратчайшие расстояния между центрами окружностей, а контуры, вписанные в окружности, также будут иметь минимальные размеры. Образование правильных шестиугольников в этой сети возможно как частный случай. Таким образом, для каждого варианта разрезки оптимальное решение по минимуму материала (длины элементов) – это размещение шестиугольников, вписанных в окружности, причем в первом оптимальном варианте смежные три окружности касаются друг друга. Каждое оптимизационное решение по другим критериям будет следующим за оптимальным – «постоптимальным».
Оптимизация треугольной геометрической сети на сфере по критерию минимума типоразмеров элементов может быть представлена, таким образом, как постоптимизация и решена размещением в системе неправильных шестиугольников, вписанных в окружности минимальных размеров, максимума правильных шестиугольников, например, в совместимых сферических треугольниках (сегментах) икосаэдра со схемой разрезки, показанной на рис. 1 и 2. Кроме вариантов применения свойств симметрии главных и параллельных линий окружностей сферы, в подобных разрезках должны быть реализованы возможности центральной симметрии окружностей [3, 4]. На схемах рис. 1 и 2 приведено размещение описанных окружностями шестиугольников в сферическом треугольнике (совместимом сегменте сферического икосаэдра) с внутренними углами 36, 90 и 60°. При оптимизации треугольной сети с помощью симметрии окружностей и главных линий сферы можно выделить как одну из промежуточных задач – определение положения центров окружностей шестиугольников (рис. 1: центры первых рядов шестиугольников О1, О2). Переход от неправильных к правильным шестиугольникам, вписанным в окружности, проведем на примере разрезки в виде 1280-гранника (рис. 2).
Итак, на первом этапе определяем положение центров О1, О2 шестиугольников равных радиусов в сферическом треугольнике (совместимом сегменте сферы с разрезкой 1280-гранника (рис. 1)) у внутреннего угла 60 градусов. Введя обозначения r = r1,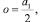 
A = A1 и используя теоремы синусов и косинусов для треугольников, получаем систему уравнений (1):
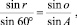
cosA = sin 60°∙coso, (1)
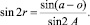
Параметры прямоугольного сферического треугольника (рис. 1) с катетами r1 и a1 определяются из системы уравнений (1).
Катеты и гипотенузы рассматриваемых сферических треугольников связаны соотношениями
tgr = tgr1∙cosA,
tgo = tgr1∙cos60°, (2)
tgr = tgr∙cos2A.
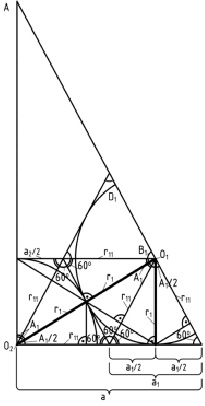
Рис. 1. Определение положения центров О1 и О2 шестиугольников (толстые линии) равных радиусов в сферическом треугольнике с внутренними углами 90–60°. Углы даны для схемы-первоосновы расположения центров, показанной тонкими линиями, т.е. для касающихся окружностей, описывающих неправильные шестиугольники равных радиусов
Таким образом, из уравнений (2) можно определить зависимость параметров o и A (рис. 1), позволяющую определить центр окружности O1.
Проведя некоторые преобразования, имеем
tg2r = 1 – cos2A,
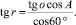
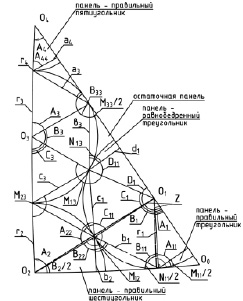
Рис. 2. Совместимый сегмент сборной сферической оболочки в виде 1280-гранника: Оо – центр панели в виде правильного треугольника на сфере; О1, О2, О3 – центры панелей в виде плоских шестиугольников; О4 – центр панели в виде правильного плоского пятиугольника; А2 – обозначение внутреннего угла первого по часовой стрелке треугольника в шестиугольнике у центра О2; b1 – обозначение полярного угла дуги второго по часовой стрелке треугольника в шестиугольнике против центра О1;Mii, Nii. – внутренние углы между соответствующими i – шестиугольниками
Отсюда приходим к уравнению
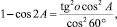
которое приводится к виду
3tg2A – 1 = 4tg2o. (3)
Теперь определим зависимость параметров o и a. Исходя из уравнений (1), получаем
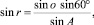
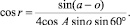
Используя основное тригонометрическое тождество, исключаем параметр r:
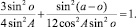
Откуда получаем уравнение
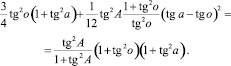
Так как из (3)
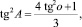
то искомое соотношение принимает вид
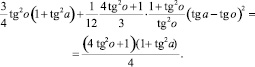
Наконец, введя обозначения
ka = tga, t = tgo,
и проведя некоторые преобразования, приходим к уравнению
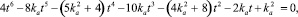
которое приводится к виду
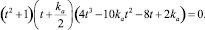(4)
По условию задачи находятся только положительные корни уравнения (4), а следовательно, искомое решение найдем из уравнения третьей степени
2t3 – 5kat2 – 4t + ka = 0. (5)
Проводим вычисления для параметра a = 20,905162886°, получаем значение параметра ka = 0,3819661. Корни уравнения (5) имеют вид
t1 = 1,9366878;
t2 = –1,0736234;
t3 = 0,0918509.
Искомое решение определяем, исходя из корня t3:
o = 5,2479437°,
A = 30,413417°.
«Постоптимизация» по критерию минимума типоразмеров элементов может быть проведена размещением в системе неправильных шестиугольников, вписанных в окружности минимальных размеров с центрами О1 и О2, максимума правильных шестиугольников (рис. 2). Целевая функция будет выглядеть как минимум среднеквадратического отклонения центральных внутренних углов только шестиугольников (без правильного пятиугольника) по отношению к углу 60°.
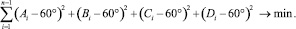(6)
Углы Ai, Bi, … связаны соотношениями, подобными (1)–(5), т.е. окружности, в которые вписаны шестиугольники, либо касаются, либо пересекаются.
Здесь Ai, Bi, … – внутренние углы соответствующих i-шестиугольников, размещенных в сегменте (рис. 2). Оптимальное значение отклонений углов для пары шестиугольников, вписанных в окружности с неизменным расположением их центров, показано для схемы разрезки на рис. 2 (первоначальное положение радиусов показано здесь пунктиром) и очевидно равно:
A1 – 60° = A2 – 60° = –0,826834°,
B1 – 60° = –0,826834°,
B2 – 60° = –0,413417°,
C2 – 60° = 0,413417°,
D2 – 60° = 0.
Таким образом, сложные задачи со многими центрами можно упростить разбиением шестиугольников на группы и применением метода итераций. Для решения уравнения (5) использовалось свободно распространяющееся программное обеспечение Sclab 5.4.1 – The free platform for Numerical Computation (аналог Matlab) [7].
Выводы
Полученные решения позволят реализовать алгоритмы аппроксимации сферы треугольной геометрической сетью с максимальным числом правильных шестиугольников и подготовить варианты оптимизации разрезок сферы.
Рецензенты:
Колчунов В.И., д.т.н., профессор, академик РААСН, г. Москва;
Кондращенко В.И., д.т.н., профессор кафедры «Строительные материалы и технологии», ФГБОУ ВПО «Московский государственный университет путей сообщения», г. Москва.
Работа поступила в редакцию 06.11.2014.
Библиографическая ссылка
Антошкин В.Д., Никонов В.И. К ВОПРОСУ ОПТИМИЗАЦИИ ТРЕУГОЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ СЕТИ НА СФЕРЕ // Фундаментальные исследования. 2014. № 11-8. С. 1669-1673;URL: https://fundamental-research.ru/ru/article/view?id=35824 (дата обращения: 05.04.2025).