Постоянный рост требований, предъявляемых к качеству выпускаемой промышленной продукции, определяет соответствующие требования по точности и быстродействию отработки заданных законов и траекторий движения следящих ЭМСУ. Как известно из теории автоматического управления, задача получения требуемых динамических показателей качества решается путем введения в систему специальных корректирующих устройств. Применение таких корректирующих устройств позволяет обеспечить инвариантность системы электропривода по управляющему и возмущающему воздействию, а также поднять порядок астатизма.
Большинство современных следящих электроприводов являются сложными многоконтурными системами с обратной связью по нескольким координатам электропривода [3, 7]. При проектировании электроприводов, имеющих многоконтурную структуру с последовательной коррекцией, наибольшее распространение получили методики, использующие типовые настройки вложенных друг в друга контуров регулирования на модульный или симметричный оптимумы [1, 2]. Однако такой подход приводит к затягиванию процессов регулирования выходной переменной при увеличении числа подчиненных контуров регулирования и делает практически невозможным быстродействующее управление следящими ЭМСУ с упругими связями.
В связи с этим возникает необходимость применения новых способов построения ЭМСУ и синтеза алгоритмов цифрового управления электроприводами, в частности на основе применения критерия предельного быстродействия и контроля полного вектора состояния объекта управления, обеспечивающих плавное движение исполнительного органа при максимальном быстродействии [5]. В качестве критерия оптимизации представляется целесообразным применить критерий предельного быстродействия, который в детерминированных дискретных линейных системах обеспечивает одновременно минимум интегральной динамической ошибки управления при отсутствии перерегулирования выходной координаты [5, 6].
В качестве метода синтеза оптимального дискретного (цифрового) управления можно воспользоваться методом модального управления при расположении корней характеристического уравнения замкнутой системы заведомо на отрицательной вещественной полуоси [6] или методом синтеза цифровых апериодических регуляторов состояния [5].
Объект управления при этом представим в виде
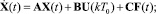(1)
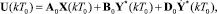(2)
где оптимальное управление U(kT0) представлено в виде линейной формы полного контролируемого вектора состояния, заданного состояния выходной переменной и ее производной.
Искомые матрицы A0, B0, D0 определены в результате проведения процедуры синтеза [4, 5] для некоторого заведомо заданного такта дискретного управления. В частности, при такте T0 = 0,01 с эти матрицы имеют вид
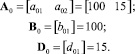(3)
На рис. 1 приведена схема моделирования динамики следящей электромеханической системы управления, соответствующей структурам и параметрам моделей объекта управления и устройства управления, приведенным выше. При этом замкнутый контур момента на валу электропривода представлен апериодическим звеном первого порядка с постоянной времени 0,01 с и единичным коэффициентом передачи. Квазиинвариантность системы по задающим воздействиям обеспечивается формированием задания сразу по двум фазовым переменным – положению и скорости ЭМСУ.
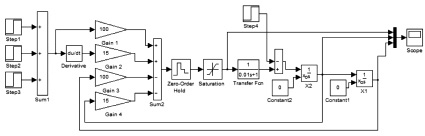
Рис. 1. Схема моделирования дискретно-непрерывной ЭМСУ
В качестве тестовых воздействий на систему приняты 3 последовательных (в моменты времени t = 0, t = 1 и t = 3 с) и на порядок возрастающих по амплитуде ступенчатых воздействиях приращений положения (0,1; 0,9 и 9,0 рад). Уровень ограничения дискретного регулятора состояния примем равным 10 В.
Результаты моделирования приведены на рис. 2. Графики отражают переходные процессы координат ЭМСУ: U(kT0) – дискретное управление (В); ω – угловая скорость вращения электродвигателя (рад./с); φ – угловое перемещение (рад).
Анализ полученных переходных процессов позволяет сделать вывод, что при увеличении задания на входе ЭМСУ происходит насыщение координаты управлении на уровне 10 В уже при задании положения 1 рад., что делает систему нелинейной. При этом дальнейшее увеличение приращения задания положения до 10 рад. приводит к недопустимому колебанию фазовых переменных ЭМСУ.
Рассмотрим класс следящих систем, где перемещение рабочего органа задается последовательностью приращений перемещений во времени по той или иной координатной оси, реализуя на уровне задания небольшие ступенчатые во времени переходы. В этом случае вместо интерполяторов нулевого порядка достаточно применения эталонных моделей (ЭМ) или задатчиков интенсивности (предшествующих фильтров), обеспечивающих ограничения фазовых переменных ЭМСУ на допустимых уровнях при произвольных по величине приращениях задающих воздействий. При этом важно не допустить работу ЭМСУ в нелинейной зоне, требующую применения нелинейных регуляторов, процедура синтеза которых и программная реализация достаточно трудоемки.
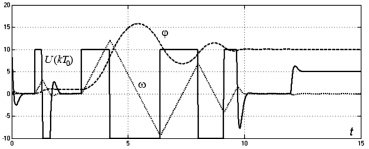
Рис. 2. Переходные процессы в дискретно-непрерывной ЭМСУ (T0 = 0,01 с)
Именно этой цели и служат линейные и нелинейные дискретно-непрерывные ЭМ, вопросы использования которых при синтезе ЭМСУ рассмотрим ниже. Будем полагать, что главным техническим критерием при отработке эталонной моделью приращений заданных перемещений является минимум времени перехода при минимуме интегральной погрешности изменения выходной координаты. Однако при этом линейные ЭМ обладают недостатками, ограничивающими их применение в следящих системах [3, 7]. В связи с этим далее предлагается рассмотреть синтез ЭМСУ с нелинейной адаптивной дискретно-непрерывной эталонной моделью.
На рис. 3 представлена структурная схема системы управления с дискретно-непрерывной нелинейной ЭМ второго порядка.
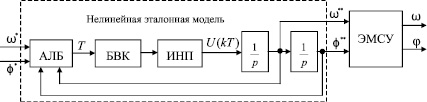
Рис. 3. Структура системы управления с нелинейной адаптивной эталонной моделью
На рисунке приняты следующие обозначения: АЛБ – арифметико-логический блок, БВК – блок вычисления коэффициентов эталонной модели в функции такта управления, ИНП – интерполятор нулевого порядка, ЭМСУ – электромеханическая система управления.
Подобъект управления в рассматриваемой ЭМ представлен последовательным соединением интегрирующих звеньев, а устройство управления представляет собой дискретный регулятор состояния. Выходные координаты ЭМ формируют задание углового положения и угловой скорости на входе ЭМСУ.
Дискретно-непрерывная линейная математическая модель ЭМ, представленная на рис. 3, может быть записана в векторно-матричной форме [4, 5]:
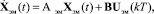(4)
где Xэм(t) – вектор фазовых переменных модели,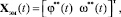 
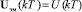– скалярное управляющее воздействие ЭМ, 
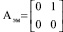– матрица состояния ЭМ, 
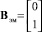– матрица управления ЭМ.
Для определения оптимальной по критерию быстродействия ЭМ (4) воспользуемся методикой, приведенной в [4, 5]. В соответствии с концепцией терминальных систем управления в выражении (4) обеспечивается одновременно максимум быстродействия и минимум интегральной ошибки отработки ступенчатых задающих воздействий. Следовательно, согласно методике синтеза [4, 5] представим это выражение в виде линейной формы координат состояния, задающих воздействий и их производных, изменяемых в дискретные моменты времени с периодом квантования T:
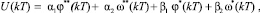(5)
где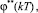 
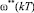– фазовые переменные ЭМ;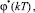 
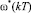– задающие воздействия фазовых переменных ЭМ; α1, β1, α2, β2 – коэффициенты ЭМ, полученные в результате оптимизационной процедуры синтеза [4, 5].
Несложные математические преобразования позволили установить зависимость оптимальных параметров синтезированного устройства управления ЭМ (значений коэффициентов α1, β1, α2, β2) от такта управления T. Для рассматриваемой эталонной модели второго порядка имеем
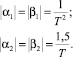(6)
Теперь необходимо найти алгоритм вычисления такта T в функции задающих воздействий φ* и ω* при ограничениях на управление U(kT):
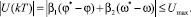(7)
Подставляя выражения (6) в неравенство (7), получаем
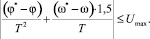(8)
В частном случае полагая, что ω* = 0 и T = 0,1 с, a Umax = 10 В, имеем неравенство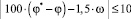 
, из которого, задавшись нулевыми начальными условиями (ω(0) = φ*(0) = 0), можно получить, что 
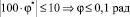и сделать вывод, что величина такта T определяется выражением
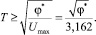
Полученная в результате синтеза схема ЭМСУ с нелинейной дискретно-непрерывной эталонной моделью 2-го порядка приведена на рис. 4.
Из графиков переходных процессов (рис. 5) видно, что в синтезированной системе управления отсутствуют недостатки, выявленные в дискретно-непрерывной ЭМСУ без эталонной модели.
Анализируя полученные результаты моделирования, стоит отметить ряд достоинств синтезированной системы управления с нелинейной дискретно-непрерывной ЭМ:
– нелинейная ЭМ используется в качестве предшествующего фильтра, вынесенного за замкнутую ЭМСУ, а следовательно, не влияет на устойчивость и показатели качества самой ЭМСУ;
– эталонная модель обеспечивает адаптацию ЭМСУ к энергетическим ресурсам и требованиям технологического процесса за счет ограничения фазовых переменных на уровнях, позволяющих системе функционировать в линейной зоне при любых задающих воздействиях;
– для синтеза ЭМСУ может быть использована линейная теория управления, и структура регулятора самой ЭМСУ при этом будет линейной, т.е. может быть использован любой типовой аналоговый или дискретный регулятор класса «вход-выход» (П, ПИ, ПИД и др.), а не только рассмотренный выше дискретный регулятор состояния;
– коррекцией параметров ЭМ легко добиться отсутствия перерегулирования выходной переменной во всем диапазоне изменения приращения ее задания.
Из недостатков стоит отметить снижение быстродействия системы при увеличении величины задания на входе ЭМ, что ограничивает область применения ЭМ, в частности, в позиционно-траекторных ЭМСУ, где целесообразно реализовать работу системы на предельных значениях внутренних фазовых переменных (скорости и ускорении). Однако применительно к классу следящих ЭМСУ, функционирующих исключительно или преимущественно в зоне малых отклонений координат, такой подход более чем оправдан.
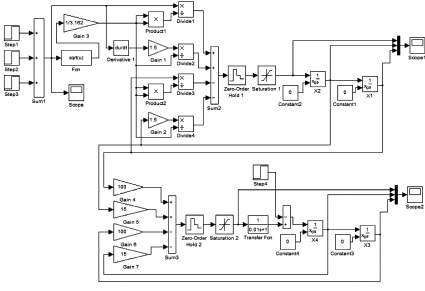
Рис. 4. Схема моделирования дискретно-непрерывной ЭМСУ c нелинейной адаптивной эталонной моделью
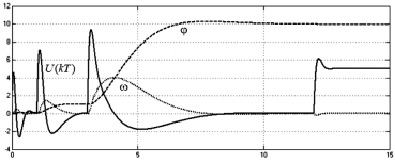
Рис. 5. Переходные процессы в дискретно-непрерывной ЭМСУ c нелинейной адаптивной эталонной моделью
Результаты рассмотренных в работе исследований в дальнейшем могут быть положены в основу методики синтеза программных, следящих и адаптивных электромеханических систем управления с такого рода эталонными моделями.
Рецензенты:
Бочкарев С.В., д.т.н., доцент, профессор кафедры микропроцессорных средств автоматизации, Пермский национальный исследовательский политехнический университет, г. Пермь;
Цаплин А.И., д.т.н., профессор, зав. кафедрой общей физики, Пермский национальный исследовательский политехнический университет, г. Пермь.
Работа поступила в редакцию 06.11.2014.
Библиографическая ссылка
Даденков Д.А., Казанцев В.П. СИНТЕЗ ЭЛЕКТРОМЕХАНИЧЕСКИХ СИСТЕМ УПРАВЛЕНИЯ С НЕЛИНЕЙНОЙ АДАПТИВНОЙ ЭТАЛОННОЙ МОДЕЛЬЮ // Фундаментальные исследования. – 2014. – № 11-7. – С. 1466-1471;URL: https://fundamental-research.ru/ru/article/view?id=35788 (дата обращения: 03.12.2024).