Целью работы является выявление факторов, влияющих на формирование водного баланса, основных подсистем системного комплекса и их взаимосвязей и разработка на этой основе информационно-технологической модели, позволяющей произвести имитационное моделирование и получить характеристики водного баланса речного бассейна.
В работе решаются следующие задачи:
– разработка модели водного баланса речного бассейна и построение системной диаграммы в обозначениях Дж. Форрестера [5];
– формирование системы уравнений подсистем системного комплекса в аналитической форме;
– построение расчетного имитационного комплекса в прикладной программной среде MathCAD;
– проведение имитационного эксперимента.
Современная концепция оценки экологического состояния природных вод основана на составлении линейных водобалансных моделей [1-5], в которые явно или неявно входят основные физические подсистемы [4]:
– подсистема, связанная с осадками и испарением влаги;
– подсистема динамики поверхностных вод;
– подсистема фильтрационного движения грунтовых вод.
Линейный характер всех указанных подсистем позволяет составить единую системную методику оценки состояния водных ресурсов и планирования их использования на основе динамической балансовой модели Дж. Форрестера [5]. Форрестеровская модель отражает инерционность реальных систем, которая ведет к задержке изменений в отдельном элементе, передаваемых другими элементами системы.
Контуры связи систем представляют собой функции запаздывания. Каналы потоков субстанций, протекающих в системе, формируют некоторые уровни их накопления, которые регулируются темпами или функциями решения. Соединение уровней с функциями решения информационными связями обеспечивает необходимое по условиям описания реального процесса единство между подсистемами, входящими в систему (рис. 1).
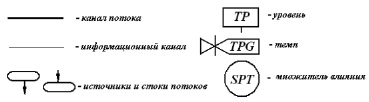
Рис. 1. Обозначения, принятые в модели Дж. Форрестера [5]
Имитационное моделирование
На основе балансовых динамических моделей Дж. Форрестера [5] построена системная модель водного баланса речного бассейна, включающая три основные физические подсистемы (рис. 2).
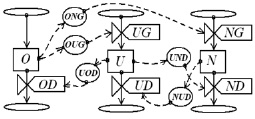
Рис. 2. Системная диаграмма водобалансной модели
Элементы системы обозначаются индивидуальными именами – идентификаторами. Для системы состояния водных ресурсов идентификаторы приведены в таблице (табл. 1). Величины, приведенные в таблице, являются условными. Прежде всего это относится к множителям влияния, которые требуют установления уравнений связи на основе данных наблюдений.
Системная диаграмма позволяет составить систему уравнений уровней и темпов, в которой с помощью расширений символами J, K, L обозначаются предыдущий, текущий и будущий моменты времени, и расширений символами JK и KL – периоды, предшествующий настоящему моменту времени K и следующий за ними.
Уравнения уровней принимают вид
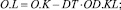 (1)
(1)
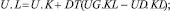 (2)
(2)
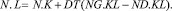 (3)
(3)
Уравнения темпов запишутся
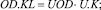 (4)
(4)
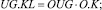 (5)
(5)
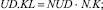 (6)
(6)
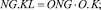 (7)
(7)
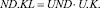 (8)
(8)
где DT – расчетный интервал времени.
Предельным переходом при DT → 0 можно перевести уравнения темпов и уровней к аналитическому виду:
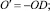 (9)
(9)
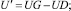 (10)
(10)
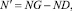 (11)
(11)
где штрихом обозначены производные по времени;
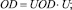 (12)
(12)
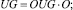 (13)
(13)
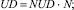 (14)
(14)
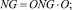 (15)
(15)
 (16)
(16)
Обозначения элементов системы состояния водных ресурсов
|
Номер элемента системы |
Идентификатор элемента системы |
Вербальное описание элемента системы |
Размерность элемента системы |
Численное значение величины элемента |
|
1 |
O |
Уровень осадков |
м |
0,005 |
|
2 |
OD |
Темп уменьшения уровня осадков |
м/сут |
0 |
|
3 |
U |
Уровень поверхностных вод |
м |
63 |
|
4 |
UG |
Темп повышения уровня поверхностных вод |
м/сут |
0,001 |
|
5 |
UD |
Темп понижения уровня поверхностных вод |
м/сут |
0 |
|
6 |
N |
Уровень грунтовых вод |
м |
2,2 |
|
7 |
NG |
Темп повышения уровня грунтовых вод |
м/сут |
0,001 |
|
8 |
ND |
Темп понижения уровня грунтовых вод |
м/сут |
0,0005 |
|
9 |
OUG |
Множитель влияния осадков на повышение уровня поверхностных вод |
1/сут |
1 |
|
10 |
UOD |
Множитель влияния поверхностных вод на понижение уровня осадков |
1/сут |
0 |
|
11 |
ONG |
Множитель влияния осадков на повышение уровня подземных вод |
1/сут |
10–3 |
|
12 |
UND |
Множитель влияния поверхностных вод на понижение уровня подземных |
1/сут |
10–6 |
|
13 |
NUD |
Множитель влияния подземных вод на понижение уровня поверхностных |
1/сут |
0 |

Рис. 3. Фрагмент листинга имитационной модели, реализованной в среде MathCAD
Полученная система уравнений является автономной. Однозначность решения полученной системы обеспечивается начальными условиями в момент времени K, следующими из уравнений темпов. Система уравнений (9)–(16) образует в принятых допущениях систему линейных однородных дифференциальных уравнений с постоянными коэффициентами.
Имитационный эксперимент
Разработанная модель водного баланса речного бассейна реализована в прикладной программной среде MathCAD. Построенный имитационный комплекс приведен в листинге программы (рис. 3).
Интерпретация результатов
Предложенная модель в целом отражает тенденцию повышения уровня поверхностных вод с течением времени при постоянном уровне осадков. Зависимость уровня грунтовых вод, напротив, имеет тенденцию к понижению. Последнее обстоятельство требует корректировки множителей влияния поверхностных вод на уровень грунтовых. В дальнейших исследованиях будет проанализирован вопрос об уточнении модели и повышении качества выводимого решения.
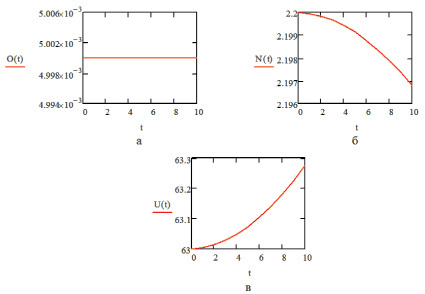
Рис. 4. Динамика основных подсистем системной модели: а – уровень осадков; б – уровень грунтовых вод; в – уровень поверхностных вод
Выводы
1. Системное моделирование с использованием балансового подхода Дж. Форрестера позволило получить модель водного баланса речного бассейна и составить ее математическое описание.
2. Путем имитационного моделирования в прикладной программной среде MathCad для условных начальных параметров построены динамические характеристики подсистем системной модели, которые могут быть уточнены для данных натурных измерений.
Рецензенты:
Полянин И.А., д.т.н., профессор, зав. кафедрой транспортно-технологических машин, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола;
Царев Е.М., д.т.н., профессор кафедры технологии и оборудования лесопромышленных производств, ФГБОУ ВПО «Поволжский государственный технологический университет», г. Йошкар-Ола.
Работа поступила в редакцию 30.10.2014.
Библиографическая ссылка
Поздеев А.Г., Кузнецова Ю.А., Ржепкин А.Ю. ИНФОРМАЦИОННО-ТЕХНОЛОГИЧЕСКАЯ МОДЕЛЬ ВОДНОГО БАЛАНСА РЕЧНОГО БАССЕЙНА // Фундаментальные исследования. 2014. № 11-6. С. 1253-1256;URL: https://fundamental-research.ru/ru/article/view?id=35709 (дата обращения: 27.12.2025).



