Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Исмагилов И.И. 1 Бичурин Р.В. 2

---

1 ФГБОУ ВПО «Казанский (Приволжский) федеральный университет» Министерства образования и науки РФ

2 ФГБОУ ВПО «Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ»

В данной работе рассматриваются основные методы прогнозирования количественных показателей сложных систем, приводятся недостатки и преимущества использования каждого из них. Предлагается классификация нечетких прогнозов, сформированных экспертами индивидуально либо в составе группы. Указывается, что полученные индивидуальные и коллективные нечеткие прогнозы могут быть агрегированы в комбинированный нечеткий прогноз. Необходимость получения комбинированного нечеткого прогноза может быть обусловлена поставленной задачей. Также в работе предложен новый метод разработки нечетких прогнозов на основе процедуры групповой экспертизы. Суть данного метода заключается в последовательном сужении исходного коллективного интервального прогнозного значения до соответствующих нечетких чисел подгруппами экспертов. Сужение осуществляется посредством сравнения приоритетов получаемых подинтервалов согласно методу Саати. В рамках данного метода были выведены аналитические выражения для вычисления приоритетов альтернатив в случае деления прогнозного интервала на три подинтервала. Построение функции принадлежности полученного нечеткого прогноза и определение его доверительного интервала осуществляется согласно эвристическому алгоритму построения функции принадлежности нечеткого числа. В рамках алгоритма реализации метода предусмотрено уменьшение количества итераций по сужению исходного прогнозного интервала посредством предварительной оценки требуемого их количества для получения нечеткого прогноза. Разработанный метод является компьютерно-ориентированным и предназначен для использования в человеко-машинных системах прогнозирования социально-экономических процессов и показателей сложных технических систем

Статья в формате PDF

1159 KB

прогнозирование

нечеткий прогноз

функция принадлежности нечеткого числа

прогнозный интервал

доверительный интервал нечеткого числа

матрица парных сравнений

1. Жариков О.Н., Королевская В.И., Хохлов С.Н. Системный подход к управлению / под ред. В.А. Персианова. – М.: ЮНИТИ – ДАНА, 2001. – 62 с.

2. Чегыркин Е.М. Статистические методы прогнозирования. – М.: Статистика, 1977. – 200 с.

3. Глущенко В.В. Менеджмент: системные основы. – 2-е изд. – М.; НПЦ – «Крылья», 1998. – 224 с.

4. Тихонов Э.Е. Методы прогнозирования в условиях рынка: учебное пособие. – Невинномысск, 2006. – 221 с.

5. Чучуева И.А. Модель прогнозирования временных рядов по выборке максимального подобия: дис. ... канд. техн. наук. – М., 2012. – 153 с.

6. Ярушкина Н.Г., Афанасьева Т.В., Перфильева И.Г. Интеллектуальный анализ временных рядов: Учебное учебное пособие. – Ульяновск: УлГТУ, 2010. – 320 с.

7. Исмагилов И.И., Зинкин В.А. Нечеткое прогнозирование количественных показателей сложных систем // Исследования по информатике. – Казань.: Отечество, 2007. – С. 49–56.

8. Заде Л.Заде. Понятие лингвистической переменной и его применение к принятию приближенных решений. – М.: Изд-во «Мир», 1976. – 149 c.

9. Борисов А.Н., Крумберг О.А., Федоров И. П. Принятие решений на основе нечетких моделей: Примеры использования. – Рига: Зинатне, 1990. – 184 с.

10. Саати Т.Саати. Принятие решений. Метод анализа иерархий: пер. с англ. Р.Г. Вачнадзе. – М.: Изд-во «Радио и связь», 1993. – 278 с.

11. Миллер Г. Миллер. Магическое число семь плюс минус два // Инженерная психология. – М.: Прогресс, 1964. – С. 564–581.

12. Чернышева Т.Ю. Иерархическая модель отбора и оценки экспертов // Доклады Томского государственного университета систем управления и радиоэлектроники. – Томск., 2009.  – С. 168 –173.

13. Shanteau J. Competence in experts // Organizational Behavior and Human Decision Processes. – Kansas, 2006. – Р. 252–-266.

14. Bagaturia G., Tabatadze M. Estimation of Expert’s Competence for the Tasks of Forecasting // Journal of Business. – 2012. – Р. 4 –9.

Прогнозирование – это один из ключевых моментов при принятии управленческих решений в современном обществе. Регулярное прогнозирование процессов позволяет не только принимать эффективные управленческие решения, но и накапливать опыт, позволяющий повысить точность и надёжность прогнозов, улучшить модели и алгоритмы прогнозирования [1].

Условно все методы прогнозирования подразделяют на две большие группы [2]:

• формализованные (фактографические);
• экспертные (интуитивные).

Зачастую к вышеперечисленным добавляют еще одну группу – комбинированные (гибридные) методы, которые представляют собой сочетание первых двух.

К фактографическим относят методы, основанные на обработке объективных данных об объекте прогнозирования. Данные методы опираются на факты, информация о которых получена. К экспертным относят методы, в которых информационной основой являются мнения экспертов (специалистов в соответствующей области), опирающихся на их знания, интуицию и опыт.

В настоящее время насчитывается уже несколько сотен методов прогнозирования. Преимущества и недостатки широко распространенных методов, используемых для прогнозирования количественных показателей сложных систем, представлены в таблице [3, 4, 5]:

Обоснованность прогноза в значительной мере зависит от выбора метода прогнозирования, посредством которого он был получен. Фактографические методы превосходят экспертные по точности прогнозирования, так как опираются на математический инструментарий, но существенно уступают вторым в условиях наличия неопределенности в исходной информации.

Следует учесть, что ввиду значительной сложности реальных систем зачастую либо невозможно учесть влияние многих факторов, либо невозможно получить точные результаты измерений, то есть в полученных результатах присутствует определенная степень неопределенности. В таких ситуациях эффективное применение находит аппарат теории нечетких множеств. Следует также отметить, что часто прогнозируемые показатели исследуемых систем представлены временными рядами. При их прогнозировании используются следующие основные методы нечеткого прогнозирования [6]:

• методы нечеткого регрессионного анализа;
• методы нечеткого авторегрессионного анализа;
• методы нечеткого нейросетевого анализа;
• методы анализа нечетких тенденций.

Развиваются также методы нечеткого прогнозирования временных рядов на основе методов групповой экспертизы.

В данной работе предложен метод получения нечеткого прогноза, являющийся развитием метода нечеткого прогнозирования количественных показателей, представленного в [7].

Классификация нечетких прогнозов

Прежде чем приступить к описанию метода разработки нечетких прогнозов, приведем предложенную их классификацию. В данной работе нечетким прогнозом будем называть прогноз, построенный в виде нечеткого числа. Нечеткие прогнозы разделим на две группы:

1) индивидуальные (прогнозы отдельных экспертов);

2) коллективные (прогнозы группы экспертов).

Отметим, что индивидуальные прогнозы относятся к классу L-R нечетких чисел [8], а коллективные в общем случае могут и выходить за пределы этого класса нечетких чисел.

В случае коллективных нечетких прогнозов выделим 3 схемы их выработки:

1) жесткие (прогнозы строятся группой экспертов);

2) мягкие (экспертами строятся индивидуальные прогнозы);

3) комбинированные (комбинации первых двух схем).

Применение этих схем выработки прогнозов соответственно приводит к жестким, мягким и комбинированным нечетким прогнозам.

Жесткий нечеткий прогноз – нечеткое число, полученное в результате реализации определенной процедуры многотуровой групповой экспертизы.

Мягкий нечеткий прогноз – нечеткое число, полученное на основе агрегирования индивидуальных нечетких прогнозов.

Комбинированный нечеткий прогноз – нечеткое число, полученное в результате агрегирования жесткого нечеткого прогноза определенной подгруппы экспертов и индивидуальных нечетких прогнозов экспертов, не вошедших в эту подгруппу.

Введем также парциальные (частные) жесткие, мягкие и комбинированные нечеткие прогнозы, под которыми будем понимать нечеткие числа, полученные в результате агрегирования определенных групп соответствующих прогнозов.

Таким образом, в общем случае, если в результате групповой экспертизы разработаны k индивидуальных и l частных жестких нечетких прогнозов, то количество возможных вариантов построения нечетких прогнозов равно 2(k+l).

Метод нечеткого прогнозирования

В методе нечеткого прогнозирования, предложенном в [7], использован эвристический алгоритм построения функции принадлежности (ФП) нечетких чисел (чисел приблизительно равных некоторому числу K). ФП чисел, приблизительно равных некоторому числу K, строится в виде

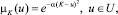
где U – универсальное множество (в общем случае – множество действительных чисел); α – параметр степени нечеткости ФП.

Величина α определяется из выражения

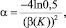
где β(K) – расстояние между точками перехода для μK(u), в которых ФП принимает значение 0,5.

Тогда выражение для ФП нечеткого числа запишется так:

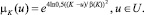
Для целочисленной переменной X, изменяющейся в пределах от 1 до 99, формулы для вычисления значений β(X) приведены в [9]. На основе этих формул в указанной работе предложен алгоритм построения ФП числа, приблизительно равного K, при произвольном натуральном числе K. С помощью данного алгоритма может быть также построена ФП в случае, когда K есть число с дробной частью, представленное в форме с плавающей запятой, при этом мантисса числа должна быть целым числом. Алгоритм применяется к мантиссе числа, а затем учитывается его порядок.

Приведем краткое описание метода нечеткого прогнозирования, основанного на использовании представленного выше известного алгоритма построения ФП нечеткого числа. Суть метода в общем случае заключается в последовательном сужении исходного коллективного интервального прогнозного значения до соответствующих нечетких чисел подгруппами экспертов.

Исходный интервал возможных значений отчета временного ряда на периоде прогнозирования устанавливается на основе групповой экспертизы определением минимального и максимального значений левой и правой границы интервала прогноза. Возможно также использование других способов определения исходного интервала прогноза. Этот интервал разбивается на s перекрывающихся на 50 % подинтервалов равной длины и проводится определение как отдельными экспертами, так и их группой нормированных приоритетов этих подинтервалов на основе метода Саати [10]. С учетом этих приоритетов подинтервалов в общем случае проводится разбиение экспертов на подгруппы и определение исходных интервалов прогноза для них. К каждому интервалу применяется итерационная процедура получения прогнозного нечеткого числа.

Итерационная процедура сужения интервала прогноза до нечеткого числа заключается в следующем. Интервал прогноза текущей итерации разбивается на s перекрывающихся на 50 % подинтервалов равной длины, и проводится определение их приоритетов. С учетом приоритетов производится сужение интервала прогноза и его сравнение с интервалом достоверности (α-срезом) нечеткого числа на заданном уровне α, в качестве среднеожидаемого которого принимается среднее значение интервала прогноза. В случае включения интервала прогноза в интервал достоверности нечеткого числа итерации прекращаются, в противном случае – проводится новая итерация по сужению интервала прогноза. Прогнозное значение показателя определяется в виде нечеткого числа, полученного на последней итерации.

Согласно алгоритму реализации метода нечеткого прогнозирования, представленного в [7], исходный прогнозный интервал делится на 3 перекрывающихся на 50 % подинтервала:

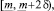
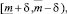
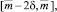
где 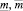– соответственно левая и правая границы интервального прогноза;

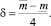
Каждая итерация данного алгоритма, основанная на процедуре групповой экспертизы, сужает исходный интервал в 2 раза. Исходя из этого, зависимость величины прогнозного интервала от номера итерации алгоритма может быть представлена следующим образом:

Δi = Δ₀2^–i , i = 1, 2, ..., n,

где Δ₀ – величина исходного прогнозного интервала; Δi – величина прогнозного интервала после i итерации алгоритма.

Аналогично для общего случая деления исходного прогнозного интервала на k равных интервала и соответственно на (s = 2k – 1) перекрывающихся на 50 % подинтервалов вышеописанное выражение запишется так:

Δ_i = Δ₀k^–i , i = 1, 2, ..., n.

Определение оценки максимального числа итераций сужения интервала прогноза найдем из условия вложенности прогнозных значений в доверительные интервалы трех нечетких чисел, построенных на граничных и серединной точках исходного интервального прогноза. Эти условия имеют вид

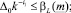
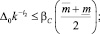
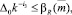i = 1, 2, ..., n,

где 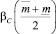, 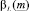и 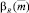– доверительные интервалы соответствующих нечетких чисел.

Приравняв и прологарифмировав левые и правые части данных условий, получим следующие оценки количества итераций:

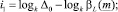
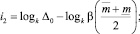
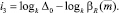
Итоговая оценка числа итераций определяется как максимальное из получившихся значений i1, i2, i3. Таким образом, может быть предварительно оценено число итераций при делении прогнозного интервала на k равных интервала.

Практический смысл данной оценки заключается в том, что, предварительно получив достаточно большое количество итераций реализации алгоритма при k = 2, мы можем с целью их уменьшения разбить прогнозный интервал на большее количество интервалов, например на 3. Тогда возникает дополнительный вопрос: «На какое максимальное число подинтервалов целесообразно делить исходный прогнозный интервал?»

В работе по инженерной психологии [11] установлено «магическое число Миллера», согласно которому эксперт способен различать 7 ± 2 градации. Значит количество подинтервалов (альтернатив) со степенью перекрытия 50 % при разбиении исходного прогнозного интервала не должно превышать число 9. Таким образом, максимальное количество равных интервалов, на которое можно разбить исходный прогнозный интервал, равно 5. Кроме того, возможен комбинированный вариант деления исходного прогнозного интервала, при этом целесообразно деление на 2 и 3 интервала. В этом случае сначала необходимо использовать разбиение на 3 интервала, а затем по мере сужения прогнозного интервала с целью повышения точности использовать деление на 2 интервала. На наш взгляд, деление на 4 и 5 равных интервалов и соответственно анализ 7 и 9 альтернатив имеет большую трудоемкость для экспертов и вычислительную сложность обработки матриц парных сравнений (МПС) альтернатив. Поэтому рациональным является деление исходного прогнозного интервала на 2 или 3 равных интервала в соответствии с ситуацией и анализ 3 или 5 альтернатив соответственно.

Ниже приведем аналитические выражения для вычисления приоритетов альтернатив методом Саати в случаях деления прогнозного интервала на 2 или 3 равных интервала. Аналитические выражения для приоритетов альтернатив выводились из следующей системы уравнений, записанной в общем виде:

AW = λW; w1 + w2 + w3 +...+ wn = 1,

где A – МПС альтернатив; W = (w1, w2, w3, ..., wn)T – вектор приоритетов; λ – максимальное собственное значение МПС альтернатив.

В случае деления прогнозного интервала на k ∈ {2, 3} равных интервалов (s ∈ {3, 5} перекрывающихся на 50 % подинтервалов) были получены следующие выражения для приоритетов альтернатив:

1) k = 2 (s = 3):

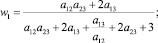
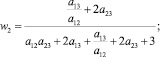
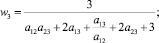
2) k = 3 (s = 5):

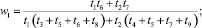
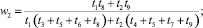
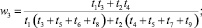
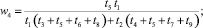
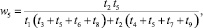
где

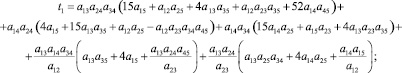
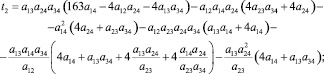
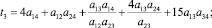
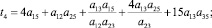
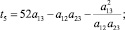
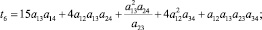
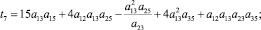
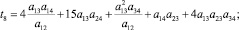
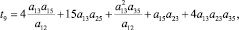
где aij – соответствующие элементы МПС.

Приведем пошаговое описание алгоритма разработанного метода нечеткого прогнозирования:

Шаг 1. Постановка задачи прогнозирования.

Шаг 2. Формирование множества экспертов размерности M: E0 = {e1, e2, ..., eM}.

Шаг 3. Определение вектора оценок компетентности экспертов:

W = {(e1w1, e2w2, ..., eMwM}).

Определение весов компетентности экспертов осуществляется известными методами [12, 13, 14].

Шаг 4. Определение на основе экспертного опроса множества:

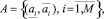
где 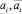– соответственно, левая и правая границы интервала прогноза i-го эксперта.

Шаг 5. Нахождение исходной групповой интервальной оценки прогнозного значения:

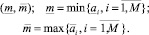
Шаг 6. Определение нечеткого числа 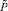«приблизительно равного 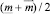» и его доверительного интервала β на уровне 0,5 ФП.

Шаг 7. Проверка вложенности интервала прогнозных значений в доверительный интервал нечеткого числа: 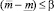. Если условие вложенности выполняется, то переход к шагу 27, иначе – к шагу 8.

Шаг 8. Предварительная оценка количества итераций сужения интервала при делении исходного прогнозного интервала на 2 равных интервала и сравнение его с предельно допустимым числом итераций, заранее заданным системным аналитиком.

Если получившаяся оценка итераций больше предельно допустимого количества итераций, то делим прогнозный интервал на 3 равных интервала. Количество получившихся альтернатив интервального прогноза в данном случае равно 5:

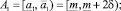
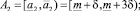
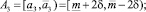
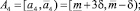
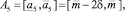
где .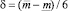

Если получившаяся оценка итераций меньше или равна предельно допустимому количеству итераций, то делим прогнозный интервал на 2 равных интервала. Количество получившихся альтернатив интервального прогноза s в данном случае равно 3:

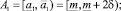
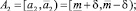
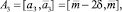
где .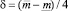

Шаг 9. Формирование экспертами индивидуальных МПС альтернатив по степени предпочтительности для определения их приоритетов для экспертов (локальных приоритетов). Аналитические выражения для вычисления приоритетов альтернатив при s = 3, 5 приведены выше.

Шаг 10. Вычисление вектора локальных приоритетов альтернатив:

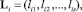
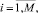s = {3, 5}.

Шаг 11. Определение локальных интервальных прогнозов:

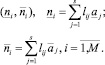
Шаг 12. Вычисление коэффициентов перекрытия локальных интервальных прогнозов Kij, 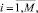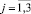со следующими интервалами:

а) s = 3:

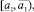
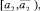
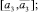
б) s = 5:

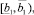
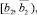
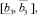
где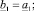

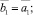
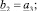
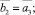
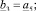
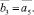
Шаг 13. Формирование подмножеств экспертов по степени их «тяготения» к базовым интервалам:

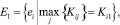
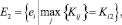
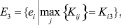
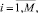
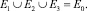
Шаг 14. Проверка условий 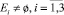. Определение группового весового коэффициента vi и выполнение для каждого непустого множества экспертов шагов 15–27.

Шаг 15. Проверка условия равенства количества экспертов в текущем их множестве 1. Если условие выполняется, то переход к шагу 16, иначе – к шагу 17.

Шаг 16. Определение группового интервального прогноза как соответствующего локального интервального прогноза и переход к шагу 20.

Шаг 17. Определение групповой МПС альтернатив путем определения ее элементов как среднегеометрических соответствующих элементов индивидуальных МПС.

Шаг 18. Вычисление вектора групповых приоритетов альтернатив:

P = (p1, p2, ..., ps), s = {3, 5}.

Шаг 19. Определение группового интервального прогноза :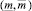

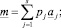
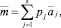s = {3, 5}.

Шаг 20. Определение нечеткого числа 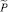«приблизительно равного 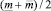» и его интервала β на уровне 0,5 ФП.

Шаг 21. Проверка вложенности интервала прогнозных значений в доверительный интервал нечеткого числа: 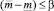. Если условие вложенности выполняется, то переход к этапу 27, иначе – к этапу 22.

Шаг 22. Предварительная оценка количества итераций дальнейшего сужения интервала прогноза. Выбор рационального количества перекрывающихся подинтервалов s ∈ {3, 5}, на которое будет поделен исходный интервал и определение альтернатив.

Шаг 23. Формирование экспертами индивидуальных МПС альтернатив по степени предпочтительности.

Шаг 24. Определение групповой МПС альтернатив путем определения ее элементов как среднегеометрических соответствующих элементов индивидуальных МПС.

Шаг 25. Вычисление вектора групповых приоритетов альтернатив:

P = (p1, p2, ..., ps), s = {3, 5}.

Шаг 26. Определение группового интервального прогноза :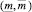

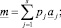
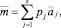s = {3, 5},

и переход к шагу 20.

Шаг 27. Определение жесткого нечеткого прогноза в виде нечеткого числа 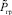и его ФП. Если на данный шаг был осуществлен переход с шага 7, то переход к шагу 29, в противном случае переход к шагу 28.

Шаг 28. Агрегирование нечетких прогнозов подгрупп экспертов с учетом весов их компетентности и получение итогового нечеткого прогноза:

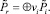
Шаг 29. Построение ФП нечеткого прогноза и определение его доверительного интервала β на уровне 0,5.

Заключение

В данной работе предложена классификация нечетких прогнозов с учетом схем их выработки. Разработан метод нечеткого прогнозирования и описан алгоритм его реализации. В этом алгоритме предусмотрено уменьшение количества итераций по сужению исходного прогнозного интервала посредством предварительной оценки требуемого их количества для получения нечеткого прогноза.

Метод нечеткого прогнозирования на основе процедуры групповой экспертизы является компьютерно-ориентированным и предназначен для использования в человеко-машинных системах прогнозирования социально-экономических процессов и показателей сложных технических систем.

Рецензенты:

Песошин В.А., д.т.н., профессор, заведующий кафедрой компьютерных систем, Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ, г. Казань;

Кирпичников А.П., д.ф.-м.н., профессор, заведующий кафедрой интеллектуальных систем и управления информационными ресурсами, Казанский национальный исследовательский технологический университет, г. Казань.

Работа поступила в редакцию 27.10.2014.

Библиографическая ссылка