В результате функционирования ПОО вокруг них формируются энергетические зоны, внутри которых существуют уровни повышенного риска для жизнедеятельности социумов ПТС системы. Случайный характер и неравномерность распределения стационарных ПОО по территории ПТС системы, а также вероятностный характер нахождения подвижных ПОО приводит к ситуациям геометрического наложения энергетических зон – образование сегментов, в которых значительно возрастает уровень риска (рис. 1).
Внутри этих зон проявляются эффекты нелинейных взаимодействий между опасными факторами различного рода ЧС [1, 2, 5, 9], вследствие чего формируются условия проявления синергетических эффектов разрушающего воздействия на режим повседневного функционирования ПТС системы от резонансной энергии ЧС.
Не ограничивая общности представлений [4, 8], в данной работе рассмотрены возможности проявления суммарного эффекта взаимодействия этих зон при оценке общего уровня техногенной нагрузки на условия жизнедеятельности ПТС системы.
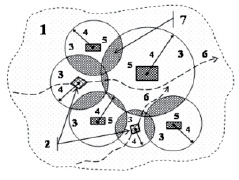
Рис. 1. Функциональная схема формирования энергетических зон повышенного риска вокруг стационарных и подвижных ПОО в виде кругов: 1 – территория размещения стационарных и подвижных ПОО; 2 – подвижные ПОО; 3 – энергетические зоны повышенного риска вокруг ПОО в процессе проявления ЧС, связанных с пожарами, взрывами и другими процессами быстрого выделения большого количества разрушающей энергии; 4 – радиусы энергетических зон повышенного риска; 5 – стационарные ПОО; 6 – трассы подвижных ПОО; 7 – зона взаимного риска от стационарных и подвижных ПОО, сформированная в процессе наложения энергетических зон повышенного риска
Математическое моделирование возможности наложения энергетических зон повышенного риска, которые формируются в виде кругов вокруг объектов в условиях существования взаимосвязей между стационарными и подвижными ПОО или – стационарными, подвижными и стационарными ПОО, выполнено в работе с учетом следующих представлений.
1. Основы моделирования территориального наложения энергетических зон повышенного риска, которые радиально формируются вокруг стационарных и подвижных ПОО. Пусть в евклидовом пространстве R2 задана область S0, которая, в общем случае, представляет собой невыпуклый многоугольник, заданный координатами вершин в глобальной системе координат. Область может описывать территорию некоторого региона, страны и т.д. Данной области принадлежат центры кругов Si(xi, yi) с фиксированными параметрами размещения (xi, yi) ∈ S0, i = 1, ..., n, а также центры кругов Sj(xj(t), yj(t)) с переменными параметрами размещения (xj(t), yj(t)), j = i + 1, ..., N, зависящими от времени t. Данные круги имеют радиусы Ri и Rj соответственно, приче, в общем случае Ri ≠ Rj, i = 1, ..., n, j = i + 1, ..., N, Ri ≠ Rk, i ≠ k, i, k ∈ {1, ..., n}, Rj ≠ Rξ, j ≠ ξ, j, ξ ∈ {n + 1, ..., N}. Каждый из кругов представляет собой область возможного опасного воздействия объекта, местоположение которого совпадает с центром соответствующего круга (как фиксированного, так и подвижного). Следует отметить, что допускается пересечение 2-х и более заданных кругов одновременно. В этой связи необходимо в любой момент времени t определить суммарную площадь пересечения Sp(xp(t), yp(t)) кругов, где p = 1, ..., N, ∀p ∈ {1, ..., n}: (xp(t), yp(t)) = (xp, yp)).
Для решения поставленной задачи необходимо в любой момент времени t, прежде всего, сформировать подмножества 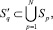 q = 1, ..., Ng, которые удовлетворяют следующим требованиям:
q = 1, ..., Ng, которые удовлетворяют следующим требованиям:
1) подмножества не пересекаются между собой, т.е. 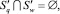 q = 1, ..., Ng – 1, w = q + 1, ..., Ng;
q = 1, ..., Ng – 1, w = q + 1, ..., Ng;
2) в пределах q-й подгруппы круги пересекаются, т.е. 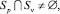
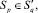
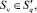 p ≠ ν, p, ν ∈ {1, ..., N}. При этом допустима и следующая ситуация:
p ≠ ν, p, ν ∈ {1, ..., N}. При этом допустима и следующая ситуация: 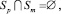
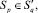
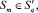 p ≠ m, p, m ∈ {1, ..., N}.
p ≠ m, p, m ∈ {1, ..., N}.
Подход к формированию подмножеств 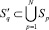 рассмотрен в работе [3].
рассмотрен в работе [3].
2. Определение в текущий момент времени tφ (φ = 1, 2, ...) площади зоны взаимного риска от стационарных и подвижных потенциально опасных объектов. Для определения в момент времени tφ суммарной площади пересечения кругов Sp(xp(t), yp(t)), p = 1, ..., N рассмотрим следующий алгоритм.
Шаг 1. Если Ng > 0, то Шаг 2, иначе – Шаг 18.
Шаг 2. q = 1 (счетчик количества подмножеств), S = 0 (суммарная площадь пересечения кругов).
Шаг 3. 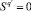 (площадь пересечения кругов в q-м подмножестве).
(площадь пересечения кругов в q-м подмножестве).
Шаг 4. Для q-го подмножества кругов определяем их точки пересечения Dc(xq,c, yq,c), C = 1, ..., Nq,c как
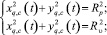 (*)
(*)
p ≠ ν; p, ν ∈ {1, ..., N};
∀p ∈ {1, ..., n}: (xp(t), yp(t)) = (xp, yp);
∀ν ∈ {1, ..., n}: (xν(t), yν(t)) = (xν, yν).
Пусть количество кругов, принадлежащих подмножеству 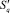 , равно Nq. Тогда количество систем уравнений вида (*), которые необходимо решить для определения всех точек пересечений кругов подмножества
, равно Nq. Тогда количество систем уравнений вида (*), которые необходимо решить для определения всех точек пересечений кругов подмножества 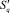 , равно
, равно 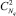 .
.
Если в результате решения системы (*) точек пересечения для некоторого круга 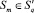 не найдено, то
не найдено, то 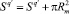 .
.
Шаг 5. Для полученного набора точек пересечения необходимо построить выпуклую оболочку 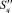 . Вычисляются параметры Aq и Bq габаритного прямоугольника для данного набора точек. В качестве начальной точки рассматривается любая точка, принадлежащая габаритному прямоугольнику. Следующий шаг – нахождение такой точки, чтобы прямая, проходящая через начальную и текущую точки, оставляла остальные точки в соответствующей полуплоскости. Таким образом, стартовой становится текущая точка, а процесс построения оболочки
. Вычисляются параметры Aq и Bq габаритного прямоугольника для данного набора точек. В качестве начальной точки рассматривается любая точка, принадлежащая габаритному прямоугольнику. Следующий шаг – нахождение такой точки, чтобы прямая, проходящая через начальную и текущую точки, оставляла остальные точки в соответствующей полуплоскости. Таким образом, стартовой становится текущая точка, а процесс построения оболочки 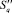 завершается при ее замыкании (рис. 2).
завершается при ее замыкании (рис. 2).
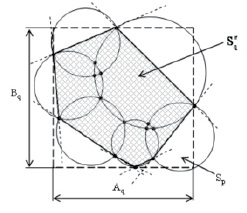
Рис. 2. Пример построения по внешним точкам пересечения в момент времени tφ энергетических зон повышенного риска от стационарных и подвижных ПОО, суммарной зоны взаимного риска в виде выпуклой оболочки 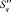
Шаг 6. Для построения границы области пересечения кругов 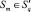 выбираем любую вершину Df(xq,f, yq,f), f ∈ {1, ..., Nq,c} выпуклой оболочки
выбираем любую вершину Df(xq,f, yq,f), f ∈ {1, ..., Nq,c} выпуклой оболочки 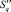 . Направление обхода границы области пересечения кругов – против часовой стрелки.
. Направление обхода границы области пересечения кругов – против часовой стрелки.
Шаг 7. Записываем координаты текущей точки построения контура T(xT, yT): xT = xq,f, yT = yq,f.
Шаг 8. Определяем набор кругов 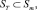
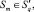 m ∈ {1, ..., N}, которым принадлежит точка T(xT, yT).
m ∈ {1, ..., N}, которым принадлежит точка T(xT, yT).
Шаг 9. Для каждого круга из ST проводим касательные LZ(T) = 0.
Шаг 10. Делаем шаг длиной δT по касательным вдоль их направляющих векторов, совпадающих с направлением обхода контура. Определяем координаты точек PZ. Исключаем из рассмотрения касательные, а также PZ, для которых точки, находящиеся на соответствующей дуге окружности на удалении δT от T(xT, yT), принадлежат только одному кругу из ST.
Шаг 11. Определяем точку 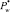 , для которой
, для которой 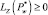 , z = 1, 2, ..., 2, w ∈ {1, 2, ...}.
, z = 1, 2, ..., 2, w ∈ {1, 2, ...}.
Шаг 12. Переходим по дуге окружности, к которой проведена касательная Lw(Pw) = 0, к ближайшей для T(xT, yT) точке из Dc(xq,c, yq,c), C = {1, ..., Nq,c}.
Шаг 13. Проверка: если граница области пересечения кругов 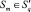 замкнута, то Шаг 15, иначе – Шаг 14.
замкнута, то Шаг 15, иначе – Шаг 14.
Шаг 14. xT = xq,c, yT = yq,c, C = {1, ..., Nq,c}. Шаг 8.
Шаг 15. Вычисляем площадь Sq области пересечения кругов 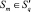 как
как 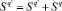 .
.
Шаг 16. 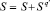 .
.
Шаг 17. q = q + 1. Если q ≤ Ng, то Шаг 3, иначе – Шаг 19.
Шаг 18. S = 0.
Шаг 19. Конец алгоритма.
Таким образом, реализация данного алгоритма позволит определять искомую суммарную площадь пересечения сформированных вокруг стационарных и подвижных ПОО в текущий момент времени tφ зон повышенного риска – кругов Sp(xp(t), yp(t)), p ∈ 1, ..., N, ∀p ∈ {1, ..., n}: (xp(t), yp(t)) = (xp, yp).
Выводы
1. В работе установлены критические зоны использования энергетического подхода [6, 7] для оценки суммарного уровня опасности жизнедеятельности территории ПТС системы, с учетом:
а) случайного распределения стационарных промышленных потенциально опасных объектов;
б) случайных маршрутов движения подвижных потенциально опасных объектов;
в) возникновения вследствие функционирования между собой стационарных и подвижных потенциально опасных объектов на критических дистанциях и взаимных чрезвычайных ситуаций техногенного происхождения.
2. Разработано математическое обеспечение (подход) для оценки суммарных зон взаимного техногенного риска от сформированных вокруг стационарных и подвижных потенциально опасных объектов радиальных зон повышенного риска, обусловленных проявлениями в них чрезвычайных ситуаций, связанных с пожарами, взрывами и другими процессами быстрого выделения большого количества разрушающей энергии.
Рецензенты:
Манохин В.Я., д.т.н., профессор кафедры пожарной и промышленной безопасности, Воронежский государственный архитектурно-строительный университет, г. Воронеж;
Мурзинов В.Л., д.т.н., доцент, профессор кафедры пожарной и промышленной безопасности, Воронежский государственный архитектурно-строительный университет, г. Воронеж.
Работа поступила в редакцию 17.10.2014.
Библиографическая ссылка
Тютюник В.В., Чапля Ю.С., Соболь А.Н., Калугин В.Д., Сушко Е.А. МОДЕЛИРОВАНИЕ ПРОЦЕССА ФОРМИРОВАНИЯ ЭНЕРГЕТИЧЕСКИХ ЗОН СУММАРНОГО РИСКА ОТ СТАЦИОНАРНЫХ И ПОДВИЖНЫХ ПОТЕНЦИАЛЬНО ОПАСНЫХ ОБЪЕКТОВ // Фундаментальные исследования. 2014. № 11-4. С. 799-803;URL: https://fundamental-research.ru/ru/article/view?id=35635 (дата обращения: 10.03.2026).



