Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Баламирзоев А.Г. 1 Баламирзоева Э.Р. 1 Курбанов К.О. 1 Гаджиева А.М. 1

---

1 Махачкалинский филиал ФГБОУ ВПО «Московский автомобильно-дорожный государственный технический университет»

В данной статье рассматривается оптимизация административной модели управления городским пассажирским транспортом на маршрутной сети города, а также задача оптимизации интервалов движения транспорта с учетом затрат времени пассажиров. При этом учтено, что большинство пассажиропотоков могут быть перевезены с помощью транспортных средств конкурирующих маршрутов. С увеличением интервала движения транспортных средств по данному маршруту возрастают затраты времени пассажиров, но сокращается ущерб от транспорта городской среде и, наоборот, при снижении интервала движения сокращаются затраты времени пассажиров, но увеличивается ущерб городской среде от работы транспорта. Предложенная модель без лишних ограничений и коэффициентов с помощью экономической оценки времени населения позволяет рассчитать оптимальное количество рейсов при любом пассажиропотоке. Приведенные критерии позволят решать задачи большой размерности, соответствующей размерам любого города.

Статья в формате PDF

705 KB

транспортное средство

модель

пассажиропоток

маршрут

интенсивность движения

оптимизация

1. Артынов А.П. Автоматизация процессов планирования и управления транспортными системами / А.П. Артынов, В.В. Скалецкий. – М.: Наука, 1981. – 272 с.

2. Баламирзоев А.Г., Алиева Х.Р., Баламирзоева Э.Р. Принятие решений пассажиропотоком по выбору маршрута передвижения//Фундаментальные исследования. – 2013. – № 4. – С. 267–271.

3. Большаков А.М. Повышение качества обслуживания пассажиров и эффективность работы автобусов / А.М. Большаков, Е.А. Кравченко, С.Л. Черникова. – М.: Транспорт, 1981. – 206 с.

4. Полак Э. Численные методы: Единый подход. – М.: Мир, 1974. – 374 с.

5. Семенова О.С. Оптимизация потоков общественного транспорта в городской среде / М.Е. Корягин, О.С. Семенова // Вопр. современной науки и практики. Университет им. В.И. Вернадского. – 2008. – Т. 1 (11). – С. 70–79.

6. Химмельблау Д. Прикладное нелинейное программирование. – М.: Мир, 1975. – 534 с.

Во многих городах общественный транспорт состоит лишь из одного вида. Как правило, это города небольших размеров. Количество транспортных операторов незначительное, перевозки убыточны, поэтому общественный транспорт управляется администрацией муниципального образования, задача которой – обеспечить равновесие между потерями времени пассажиров и ущербом от работы транспорта в городской среде.

Оптимизация интенсивности движения общественного транспорта на одном маршруте

Для составления модели необходимы следующие исходные данные: пассажиропотоки, т.е. интенсивность поступления пассажиров, которых способен перевезти данный маршрут, а также суммарная интенсивность движения транспорта других маршрутов, конкурирующих за эти пассажиропотоки. Необходимо также иметь информацию о себестоимости одного рейса и стоимости пассажиро-часа, исходя из которой для системы «город» ставится задача найти оптимальный интервал движения транспортных средств данного маршрута, обеспечивающий максимальную эффективность транспорта на маршруте в указанный период времени.

Для удобства расчетов перегруппируем пассажиропотоки по конкурирующим маршрутам, т.е. определим суммарные пассажиропотоки, перевозимые коалициями конкурирующих маршрутов:

R – количество пассажиропотоков, перевозимых транспортными средствами данного маршрута совместно с коалициями других маршрутов;

λi – интенсивность i-го потока пассажиров, перевозимого в том числе и транспортными средствами данного маршрута, ;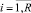

λ – интенсивность потока пассажиров, перевозимого транспортными средствами только данного маршрута;

μi – суммарная интенсивность пуассоновских потоков конкурирующих транспортных средств за i-й поток пассажиров, ;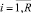

μ – интенсивность пуассоновского потока движения транспортных средств по данному маршруту;

δ – ущерб городской среде от одного рейса на данном маршруте.

Исходя из того, что потоки транспортных средств пуассоновские, не зависящие друг от друга и от потоков пассажиров, доля пассажиропотока, перевозимого каждым маршрутом, пропорциональна его интенсивности движения, т.е. доля i-го потока пассажиров, перевозимого транспортными средствами данного маршрута, равна

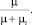
Среднее количество пассажиров, перевозимых за единицу времени транспортными средствами данного маршрута вычисляется по формуле

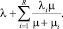
Суммарные потери пассажиров, связанные с ожиданием транспортных средств, составляют

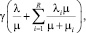(1)

а ущерб городской среде от работы транспорта –

δμ. (2)

Целью муниципалитета является поиск оптимального интервала движения транспортных средств по данному маршруту, обеспечивающего минимальные суммарные потери времени пассажиров (1) и транспортный ущерб (2):

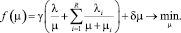(3)

При возрастании интенсивности движения целевая функция неограниченно возрастает:

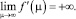
Поэтому можно ограничить интенсивность движения ГПТ по маршруту m сверху достаточно большой константой.

Вторая производная от целевой функции (3) больше нуля:

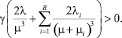
Поэтому по необходимому и достаточному условию экстремума при μ > 0 целевая функция имеет глобальный минимум при условии равенства нулю первой производной (здесь и далее: звездочкой обозначается оптимальное значение параметра):

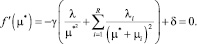(4)

В этом параграфе рассмотрена задача оптимизации интервала движения транспорта по одному маршруту с учетом затрат транспорта и социально-экономического эффекта, связанного с простоями пассажиров. Однако работа представляет в основном теоретический интерес, так как на практике необходимо осуществлять оптимизацию интервалов движения городского пассажирского транспорта по нескольким взаимодействующим маршрутам одновременно.

Численный пример

Обратим внимание на важную особенность модели на небольшом примере Рассмотрим маршрут, пассажиропоток на котором составляет 1000 чел. в час, ущерб от 1 рейса городской среде – 500 руб., средняя стоимость пассажиро-часа – 50 руб. Тогда рассчитаем оптимальное количество рейсов:

Эта формула следует из (4) при отсутствии конкурентов. Среднее время ожидания составит 6 мин, а общее время, потерянное пассажирами, 100 ч (1).

Пассажиропоток на маршрутах отличается, к тому же на одном и том же маршруте в час пик пассажиропоток может быть в разы больше, чем в раннее утреннее или позднее вечернее время. Допустим, пассажиропоток упадет в 4 раза, до 250 пассажиров. Тогда, очевидно, с точки зрения транспортного оператора необходимо пропорционально сократить количество рейсов (чтобы сохранить рентабельность). Тогда будет выполнено 2,5 рейса за час, среднее время ожидания составит 24 мин, общие потери пассажиров – 100 ч. Такое решение является несправедливым по отношению к пассажирам.

Предложенная в данной статье модель приводит к тому, что количество рейсов должно составить

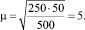
В этом случае среднее время ожидания возрастет лишь до 12 мин, а потери пассажиропотока составят 50 ч, при этом количество пассажиров, перевозимое за 1 рейс, упадет со 100 до 50. Данный подход оправдывает то, что и при малом пассажиропотоке необходимо выполнять рейсы городского пассажирского транспорта, несмотря на низкий коэффициент наполнения подвижного состава.

На практике для того чтобы добиться подобного эффекта, вводят ограничение на максимальный интервал движения городского пассажирского транспорта и максимальный коэффициент наполнения подвижного состава в часы пик и межпиковое время. Это приводит примерно к тем же результатам, что и предлагаемая в данной работе модель. Однако модель без лишних ограничений и коэффициентов с помощью экономической оценки времени населения позволяет рассчитать оптимальное количество рейсов при любом пассажиропотоке.

Оптимизация интервалов движения одного вида общественного транспорта

Построим математическую модель оптимизации работы пассажирского транспорта в городской среде. В построенной задаче существуют два критерия: потери времени пассажиров и ущерб от деятельности транспорта. Для разрешения противоречий между этими характеристиками необходимо прийти к общей размерности оценки времени пассажиров и ущерба транспорта. В данной модели для этих характеристик используется стоимостная оценка, поэтому общим критерием эффективности работы городского транспорта является суммарная стоимостная оценка социальной значимости перевозок и ущерба городской среде от эксплуатации пассажирского транспорта [1, 2, 3, 5].

Для того чтобы удовлетворить потребности каждого пассажира в перевозке, должны существовать маршруты, способные перевезти пассажира между его начальным и конечным остановочными пунктами, т.е. если

?ij > 0, то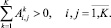

Очевидным ограничением является то, что интенсивность потоков транспортных средств, движущихся по каждому маршруту, не отрицательна:

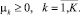(5)

Суммарный ущерб городской среде от работы городского пассажирского транспорта составит

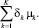(6)

Тогда средние затраты пассажиров, ожидающих транспорт на i-м остановочном пункте для переезда на j-й, в единицу времени вычисляются следующим образом:

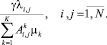(7)

Целевая функция в данной задаче представляет собой суммарные затраты транспорта на передвижение транспортных средств по маршрутам в единицу времени (6) и потери времени пассажиров в ожидании (7):

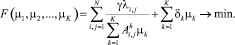(8)

Утверждение 1. Целевая функция (8) выпукла вниз по интенсивностям движения транспорта на всей области существования (5).

► Левая часть (8) является упрощенной формой функции среднего времени ожидания

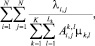
домноженной на постоянную γ, и выпукла вниз. Правая же часть линейна и при сложении не влияет на выпуклость. ◄

Утверждение 2. В задаче (5, 8) существует, и притом единственное, конечное решение.

► Целевая функция строго выпукла, при этом для каждого маршрута l

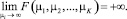(9)

Иными словами, транспортные расходы неограниченно возрастают при повышении интенсивности движения. Если зафиксируем некоторое решение 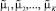, тогда оно находится в области

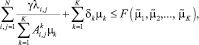
поэтому должно выполняться следующее ограничение:

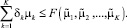
Множество, заданное данным ограничением, – выпукло и ограниченно, поэтому, исходя из этих положений, решение существует (утверждение 1), оно конечно (9) и единственно (утверждение 1). ◄

Утверждение 3. Если 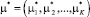(5, 8), то ущерб от работы транспорта городской среде и потери пассажиров совпадают в этой точке.

► По необходимому условию экстремума производные от целевой функции по каждому направлению равны нулю:

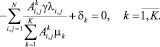(10)

Выразив α_k из (10), подставим это выражение в (8) и получим необходимый результат:

 ◄

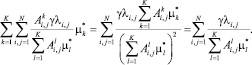Утверждение 4. Если стоимость пассажиро-часа в задаче (8) увеличится в х раз, то интенсивности движения транспорта по маршрутам должны увеличиться в 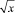раз.

► Пусть γ1 = сγ – новая стоимость пассажиро-часа, а 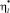 – оптимальная интенсивность движения транспорта на l-м маршруте при стоимости пассажиро-часа γ1. Тогда в точке оптимума выполняется равенство

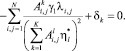(11)

Очевидно, что в данном случае при подстановке выражения

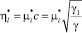
в (11) получаем (10), т.е. интенсивность движения транспорта возрастает. В аналогичной пропорции сокращается время ожидания транспорта пассажирами. ◄

Утверждение 5. Если ущерб от работы транспорта городской среде в задаче (8) увеличится в х раз, то интенсивности движения транспорта должны сократиться в 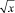раз.

Пусть 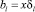 – новая стоимость одного рейса на l-м маршруте, а  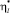– оптимальная интенсивность движения транспорта на l-м маршруте в этом случае. Тогда в точке оптимума выполняется равенство

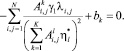(12)

Очевидно, что в данном случае при подстановке выражения

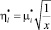
в (12) получаем (10), т.е. интенсивность движения транспорта сокращается. В аналогичной пропорции увеличивается время ожидания пассажирами. ◄

Утверждение 6. Если интенсивности пассажиропотоков в задаче (8) увеличатся в х раз, то интенсивности движения транспорта должны возрасти в 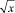раз.

►Пусть 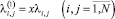 – новые интенсивности пассажиропотоков, а  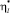– оптимальная интенсивность движения транспорта на l-м маршруте в этом случае. Тогда в точке оптимума выполняется равенство

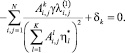(13)

Очевидно, что в данном случае при подстановке

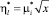
в (13) получаем (10), т.е. интенсивность движения транспорта сокращается. В аналогичной пропорции увеличивается время ожидания пассажирами. ◄

Для поиска решения данной задачи разработано множество алгоритмов [4, 6]: метод покоординатного спуска, метод Ньютона и т.д. Выпуклость критерия и его дифференцируемость на всей допустимой области позволит решать задачи большой размерности, соответствующей размерам любого города.

Рецензенты:

Агаханов Э.К., д.т.н., профессор, зав. кафедрой «Автомобильные дороги, основания и фундаменты», ФГБОУ ВПО «Дагестанский государственный технический университет», г. Махачкала;

Фаталиев Н.Г., д.т.н., профессор кафедры «Автомобильный транспорт», ФГБОУ ВПО «Дагестанский государственный аграрный университет им. М.М. Джамбулатова», г. Махачкала.

Работа поступила в редакцию 10.10.2014.

Библиографическая ссылка