Инвестиции являются одним из важнейших рычагов развития экономики предприятия. В связи с ростом научно-технического прогресса существенное значение приобретают вопросы окупаемости инвестиций во времени.
На сегодняшний день существует более 30 методов оценки инвестиционных проектов, которые условно делятся на 3 основные группы [2, 3, 4]: финансовые, качественные, вероятностные. Используя эти методы, можно рассчитать затраты в начале проекта и будущую прибыль при его завершении. В этих методах оценки инвестиционных проектов формулы расчетов приводятся с дискретами во времени с интервалами в год или в квартал, что не позволяет:
– выявить динамику развития инвестиционного процесса во времени;
– точно определить момент, когда инвестиции начнут окупаться;
– оценивать текущее состояние предприятия в любой момент времени.
Лишь в отдельных сообщениях [1, 5] делаются попытки оценок инвестиционного проекта в непрерывном времени. Однако приведенные результаты носят в значительной мере качественный характер и лишь подчеркивают актуальность углубленных исследований и оценок инвестиционных проектов в разные промежутки времени. Ниже мы воспользуемся методиками, разработанными в теории информационно-управляющих систем [6].
Введение двухпараметрической модели и ее исследование
Представим комплексный экономический параметр работы предприятия как функцию многих переменных P = φ(y1, y2, ..., yn). Раскладывая эту функцию в ряд и удерживая в рассмотрении только важнейшие факторы, схему дальнейшего анализа в первом приближении можно представить в виде (рис. 1).
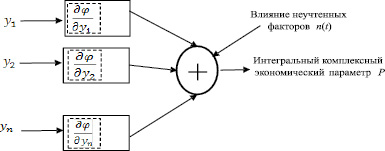
Рис. 1. К структуре модели влияющих факторов
Далее рассмотрим частный случай, когда комплексный экономический параметр работы предприятия зависит только от двух важнейших факторов, каждый из которых имеет свой канал воздействия и описывается наличием коэффициента передачи Ki (отражающим статический вклад воздействия в итоговую производительность) и динамикой (определяющей переходные процессы в ответ на входное воздействие).
Подобная модель соответствует ситуации, когда принято решение об инвестировании в новые технологии для повышения эффективности работы предприятия. При этом обучение персонала новым методам и технологиям производства должно повысить удельную производительность каждого работника, но работник часть времени должен тратить не на производственный процесс, а на обучение, что эквивалентно сокращению численности работающих.
Представим функцию, описывающую производительность предприятия, в виде
P(t) = φ(N, W, t) + n(t). (1)
Здесь обозначено N – численность работающих; W – их удельная производительность; n(t) – неучтенные факторы и воздействия. Обратим внимание, что все названные параметры рассматриваются как функция непрерывного времени t.
Используя для описания динамики весовые функции по отдельным каналам и уравнение свертки, определим (в линейном приближении) изменение производительности труда на предприятии как
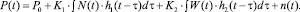 (2)
(2)
В простейшем случае динамические свойства отдельных каналов можно аппроксимировать апериодическими звеньями первого порядка:
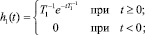
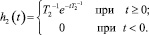 (3)
(3)
Соотношение постоянных времени отдельных каналов, а также статических коэффициентов передач существенно влияет на переходные процессы в системе. При единичных прямоугольных входных воздействиях
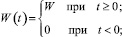
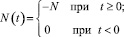
развитие процессов в системе, в соответствии с (2), (3), будет описываться выражением
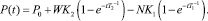 (4)
(4)
Размерность последнего выражения можно снизить, введя относительные параметры
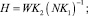
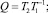
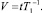 (5)
(5)
Соответствующие преобразования выражения (4) дают
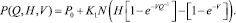 (6)
(6)
Из структуры выражения (6) (где осталось 4 параметра) видно, что произведение параметров K1N влияет только на амплитуду развития кривых, определяемых круглыми скобками.
Для относительного времени V, который входит в показатель экспоненты, диапазон рационального изменения составляет [0, 5]. Что касается двух остальных параметров, то они входят в это выражение более сложным образом.
Результаты моделирования такого выражения показали (рис. 2), что есть три группы кривых, характеризующих разное развитие инвестиционных процессов во времени.
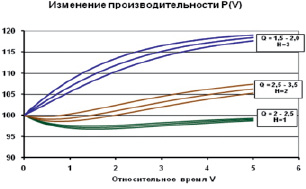
Рис. 2. Семейство кривых, характеризующих разное развитие инвестиционных процессов
Верхняя группа кривых приводит к постоянному росту производительности со старта и до установившегося значения. Это можно интерпретировать, например, как случай, когда на предприятии просто набирают новую команду, уже обладающую необходимыми навыками и более высокой удельной производительностью.
В нижней группе кривых производительность только падает и не повышается до прежнего значения. Это можно интерпретировать как случай, когда слишком много времени тратится на обучение сотрудников. Тогда запасы, накопленные ранее, постепенно истощаются и, естественно, общая эффективность не может достигнуть прежнего значения.
Наиболее типичным представляется промежуточный вариант (см. рис. 3), когда вначале производительность падает, затем достигает некоторого минимума в точке А и начинает возрастать, достигая прежней производительности в точке В и выходя, наконец, на новый более высокий уровень. Интерес представляет также срок окупаемости первоначальных затрат, т.е. время, за которое будут компенсированы потери (точка C).
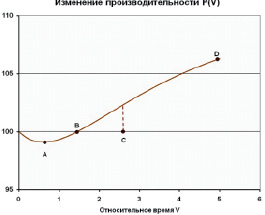
Рис. 3. Типичный процесс изменения производительности в результате инвестирования
Анализ параметров типичного процесса
Анализ полученных результатов позволяет определить важнейшие параметры развития (рис. 3) типичного инвестиционного процесса, ответив на следующие вопросы:
1. Какова величина максимального спада производительности? (см. точку А).
2. За какое время будет восстановлена прежняя производительность? (см. точку В).
3. За какое время будут компенсированы потери (срок окупаемости)? (см. точку С).
4. Какова будет максимальная производительность по окончании переходного процесса? (см. точку D).
Чтобы определить величину максимального спада производительности (в точке А) и момент, когда функция достигает минимума (абсциссу точки А), продифференцируем выражение (4) и приравняем производную к нулю:
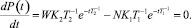 (7)
(7)
После преобразований с учетом (5) и логарифмирования можно аналитически определить момент, когда функция достигает минимума:
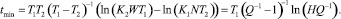 (8)
(8)
Подставляя (8) в выражение (4), получаем минимальное значение для производительности:
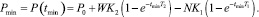 (9)
(9)
Для определения времени, за которое производительность достигает прежней величины, потребуем, чтобы P(t) = P0. Тогда из (4) следует:
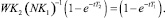 (10)
(10)
К сожалению, это трансцендентное уравнение не удается привести к замкнутому аналитическому решению, но можно искать приближенное решение, например, графически (см. рис. 4), сопоставляя расчетные значения правой и левой частей уравнения (10).
Заметим, что если K2/K1 < 1, то решение существует при T1 > T2, а когда K2/K1 > 1, то при T2 > T1. При K2 = K1 = 1 решения не существует, так как обе экспоненты выходят из одной точки и затухают с разной скоростью, какими бы ни были соотношения T2/T1.
Получим оценку сверху для времени восстановления текущей производительности. Обозначим время выхода на прежнюю производительность через tB.
Если считать, что 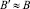 , то
, то
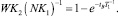
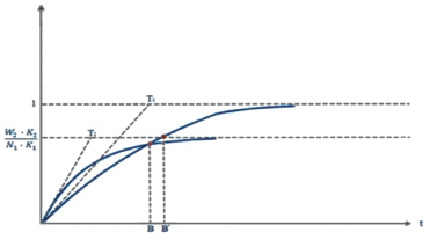
Рис. 4. Графическое нахождение точки B
После очевидных математических преобразований получаем:
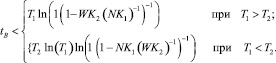 (11)
(11)
Для определения времени, за которое будут компенсированы потери, необходимо проинтегрировать выражение (4) и найти точку, в которой результат обращается в ноль. Приближенное решение нетрудно найти, принимая во внимание, что исходная производительность достигается вблизи момента времени t = 3T1 (см. точку B на рис. 4). Считая, что экспонента с показателем T1 приходит в этой точке в насыщение и далее не изменяется, разложим выражение для экспоненты с показателем T2 в ряд вблизи точки t = 3T1. Удерживая первые члены разложения, приходим к квадратному уравнению, решение которого дает значение времени для точки С в виде
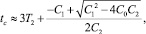 (12)
(12)
где 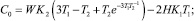 (13)
(13)
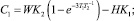 (14)
(14)
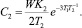 (15)
(15)
Заметим, что соотношение (15) дает «оценку снизу», т.е. компенсация потерь наступит не ранее времени, рассчитанного по этому соотношению.
Максимальная производительность по окончании переходного процесса (см. точку D на рис. 3) очевидно определится на основе выражения (4) как
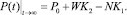 (16)
(16)
Применимость модели
Кроме ступенчатого воздействия и случайных возмущений модель способна анализировать также результаты дробных детерминированных воздействий. Модель позволяет отслеживать как единовременные воздействия (например, разовое отсутствие одного или нескольких человек, увольнение работников, плановую покупку нового оборудования), так и случайные (произвольные) изменения входных воздействий в процессе развития инвестиционного проекта (рис. 5).
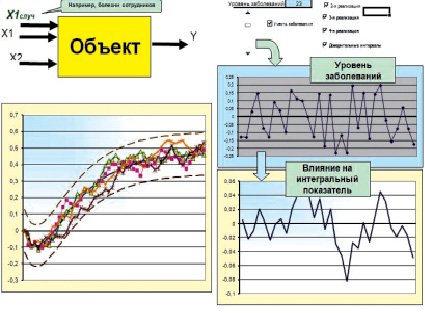
Рис. 5. Развитие инвестиционного процесса с учетом случайных воздействий
Моделирование проведено на платформе Excel + VBA, границы доверительного интервала рассчитаны в соответствии с методикой (6).
На основании результатов данной математической модели можно оценить развитие во времени и других важных экономических параметров: чистая прибыль, рентабельность инвестиционного проекта. Для этого достаточно в стандартные формулы подставить выражение для оценки производительности как функцию времени.
Заметим, что уравнение свертки позволяет рассматривать весовые функции произвольного вида, и принятая аппроксимация весовых функций в виде апериодических звеньев первого порядка сделана для достижения наглядности результатов. Учет динамики более высоких порядков требует переопределения весовых функций (3) и перерасчета интегралов (4) – (6) и последующих выражений.
Заключение
Разработанная модель дает возможность определить:
1) обобщенные количественные оценки для максимального (временного) спада производства и времени выхода на прежнюю производительность;
2) ширину интервала, на котором произошел спад производства до времени выхода на текущую производительность;
3) время восстановления, за которое будут компенсированы потери;
4) результат случайных воздействий;
5) изменения во времени важных экономических параметров предприятия (чистая прибыль, производительность), а также текущую рентабельность инвестиционного проекта.
Благодарности. Авторы выражают благодарность д.ф.-м.н. проф. Айвазяну С.А., заслуженному деятелю наук РФ, за предоставленную возможность апробации результатов путем выступления на руководимом им семинаре «Многомерный статистический анализ и вероятностное моделирование реальных процессов» в ЦЭМИ РАН.
Рецензенты:
Гагарина Л.Г., д.т.н., профессор, зав. кафедрой «Информатика и программное обеспечение вычислительных систем», НИУ МИЭТ, г. Москва;
Бондаревский А.С., д.т.н., профессор, главный научный сотрудник, ОАО «Ангстрем-М», г. Москва.
Работа поступила в редакцию 01.10.2014.
Библиографическая ссылка
Лебедев А.В., Трояновский В.М. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ РАЗВИТИЯ ИНВЕСТИЦИОННОГО ПРОЦЕССА В НЕПРЕРЫВНОМ ВРЕМЕНИ // Фундаментальные исследования. 2014. № 11-1. С. 61-67;URL: https://fundamental-research.ru/ru/article/view?id=35478 (дата обращения: 12.03.2026).



