Пусть X - сепарабельное банахово пространство с элементами x и нормой 
, 
- сопряжённое пространство, 
-основное вероятностное пространство. Через 
обозначается банахово пространство случайных элементов со значениями в Х и с нормой
.
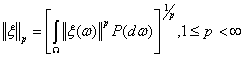Говорят, что банахово пространство X является Ga- пространством для некоторого 
, если существуют отображение 
и константа A>0 со свойствами:
1) 
2) 
3) 
для любых 
.
Примерами Ga-пространств могут служить 
-пространства, когда 
. Нами доказана
Теорема. Пусть X является Ga- пространством. Тогда для того, чтобы из ограниченной в 
последовательности 
можно было извлечь подпоследовательность 
такую, чтобы ряд 
сходился в и почти наверное, как только 
, необходимо и достаточно существование подпоследовательности слабо сходящейся в к нулю.
Библиографическая ссылка
Кобзев В.Н. К ВОПРОСУ СХОДИМОСТИ РЯДОВ ФУНКЦИЙ СО ЗНАЧЕНИЯМИ В Ga- ПРОСТРАНСТВАХ // Фундаментальные исследования. 2008. № 7. С. 116-116;URL: https://fundamental-research.ru/ru/article/view?id=3545 (дата обращения: 02.04.2025).