В микрогетерогенной среде с различными показателями преломления компонентов на микрочастицы в электромагнитном поле действуют электрострикционные силы, которые могут быть причиной возникновения концентрационных потоков. В зависимости от знака поляризуемости микрочастицы могут втягиваться (если показатель преломления вещества дисперсной фазы больше, чем дисперсионной среды) или выталкиваться (в обратном случае) из областей с большей напряженностью электрического поля электромагнитной волны, что приводит к соответствующей пространственной модуляции оптических свойств среды. Данный механизм может быть использован для записи динамических голограмм в дисперсных средах [1–4, 8–15]. Концентрационная нелинейность исследовалась экспериментально и теоретически в различных средах: газах, суспензиях, микроэмульсиях [3, 12].
Целью данной работы является теоретический анализ эффективности записи динамических голограмм при больших интенсивностях излучения, когда, в отличие от работ [3–12], изменение концентрации не обязательно мало.
В качестве дисперсной системы мы будем рассматривать прозрачную жидкофазную среду с наночастицами, находящуюся под воздействием лазерного облучения. Пусть распределение интенсивности падающего излучения в плоскости слоя среды имеет вид (такое распределение возникает при интерференции двух плоских волн)
, 
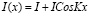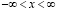, (1)
где I – интенсивность световой волны,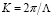 
– волновой вектор интерференционной решетки, 
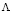– ее период, x – координата в плоскости слоя среды. Балансное уравнение, описывающее динамику концентрации наночастиц в жидкофазной среде с учётом диффузионного и электрострикционного потоков, можно записать в виде [4]
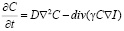. (2)
Здесь приняты следующие обозначения: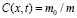 
– массовая концентрация дисперсных частиц (m0 – масса наночастиц, m-масса среды), D – коэффициент диффузии, 
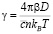, b – поляризуемость частиц, kB – постоянная Больцмана, n – эффективный показатель преломления среды, 
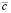– скорость света в вакууме.
Для малых изменений концентрации частиц можно представить искомую концентрацию в виде суммы невозмущенной части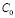 
и возмущенной 
:
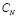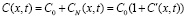, (3)
где 
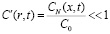. (4)
Далее мы опускаем также, учитывая его малость, слагаемое ~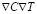
(сравнивая слагаемые 
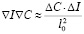и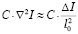 
, получаем 
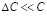, что подтверждает правомерность используемого приближения).
В итоге получим задачу:
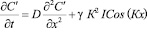, (5)
решение которой будем искать в виде
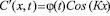. (6)
После подстановки (6) в уравнение (5) переменные разделяются. Решая получившееся уравнение относительно функции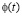 
и проводя соответствующие преобразования, получим искомое выражение для 
:
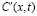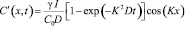. (7)
Для стационарного режима, используя (3–5), получаем:
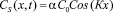. (8)
Физический смысл параметра α становится понятным при введении интенсивности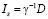 
– интенсивность насыщения, при которой изменение концентрации становится сравнимым с начальной ее величиной. Безразмерный параметр 
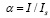показывает превышение интенсивности над интенсивностью насыщения, когда 
.
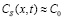В приближении малых интенсивностей амплитуда модуляции концентрации дисперсных частиц прямо пропорциональна интенсивности излучения. Поэтому нелинейные свойства среды можно описывать коэффициентом кубичной нелинейности n2 = (∂n/∂I).
Для частиц с радиусом, много меньшим длины волны излучения l, эффективный показатель преломления среды пропорционален концентрации частиц [11]:
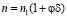, (9)
где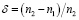 
; n1 и n2 – показатели преломления вещества дисперсионной среды и дисперсной фазы соответственно, φ = (4/3)πr3, С – объемная доля дисперсной среды, r – радиус микрочастиц.
Тогда эффективный параметр кубичной нелинейности среды:
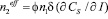. (10)
Для суспензии латексных частиц (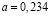
мкм) в воде экспериментально получен коэффициент нелинейности среды 
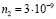см2/Вт. При использовании критической микроэмульсии в качестве нелинейной среды при 
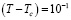K достигнута величина параметра нелинейности 
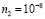см2/Вт [14]. Последний параметр позволяет рассчитать дифракционную эффективность голограммы.
Дифракционной эффективностью голограммы называется отношение [11]:
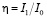, (11)
где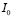 
– интенсивность падающего на голограмму считывающего луча; 
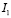– интенсивность света, продифрагировавшего в первый порядок дифракции на голограмме, представляющей собой обычно простую косинусоидальную решетку.
Для дифракционной эффективности тонких фазовых голограмм имеем [1]:
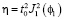, (12)
где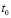 
– амплитудное пропускание неэкспонированного слоя; 
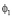– амплитуда модуляции фазового пропускания, 
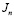> – бесселева функция n-го порядка. Полагая среду прозрачной и амплитуду фазовой модуляции малой, имеем:
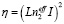, (13)
где – толщина слоя нелинейной среды. Для немалых изменений концентрации частиц, когда разложение (3) неприемлемо, уравнение (2) аналитически решается только в стационарном режиме:
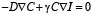. (14)
Общее решение уравнения (3) ищем в виде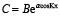 
, где В – константа. Для больших изменений концентрации частиц имеем 
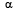>>1. Константу В находим из условия нормировки (сохранения числа частиц)
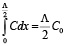. (15)
Окончательно получаем выражение для зависимости концентрации частиц от приведенной координаты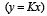 
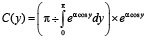. (16)
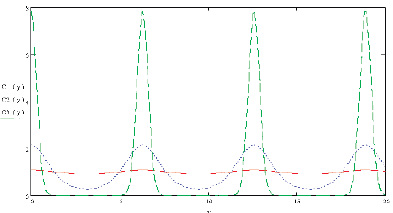
Рис. 1. Электрострикционные решетки для стационарного случая при разных интенсивностях излучения где (С1(у) = С/С0 при α1; С2(у) = С/С0 при α2; С3(у) = С/С0 при α3)
Для численного расчета амплитуды концентрационных решеток по формуле (16) использовался Mathcad. Полученные зависимости для разных интенсивностей (α1 = 0,1; α2 = 1; α3 = 10) приведены на pис. 1.
Видно, что для больших интенсивностей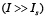 
решетка концентраций существенно несинусоидальна, что приводит к искажению профиля записываемой решетки (или появлению дополнительных дифракционных порядков).
Для анализа дифракционной эффективности голограмм рассмотрим Фурье-компоненты полученных несинусоидальных голограмм. Воспользуемся разложением в ряд Фурье для C(y):
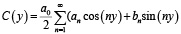, (17)
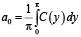, (18)
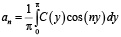, (19)
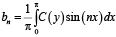, (20)
где числа a0, an и bn (n = 1,2..) коэффициенты Фурье.
Для нахождения зависимости an от параметра α вычисляем интегралы (в среде Mathcad):
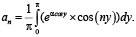(21)
На рис. 2 показаны полученные зависимости амплитуд первых четырех гармоник an концентрационной решетки от параметра α. Видно, что амплитуды первых гармоник линейно возрастают с пара метром α.
Дифракционную эффективность записанной голограммы (для 1-й фурье-компоненты) можно рассчитать, используя полученные расчетные данные (рис. 2):
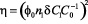. (22)
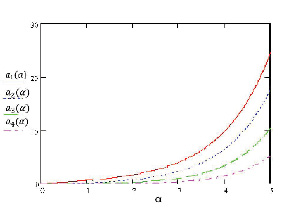
Рис. 2. Зависимости фурье–компонент концентрационной решетки от параметра α (a1(a) – первая гармоника, a2(a) – вторая гармоника, a3(a) –третья гармоника, a4(a) –четвертая гармоника)
Поскольку амплитуда модуляции почти экспоненциально растет с увеличением интенсивности, то можно ожидать значительного увеличения эффективности записи голограмм при интенсивностях больше интенсивности насыщения. Максимальная интенсивность Imax соответствует максимально достижимой концентрации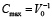 
, где V0 – объем одной частицы (т.е. объемная доля частиц Φ = 1):
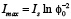(23)
где Φ0 – начальная объемная доля частиц. Поскольку обычно Φ0 << 1, то максимальная интенсивность может быть намного больше интенсивности насыщения, что представляет особенный интерес для импульсных режимов записи голограмм в дисперсных средах.
Выводы
Таким образом, показано, что при больших интенсивностях излучения запись динамической голограммы происходит в существенно нелинейном режиме, когда фазовая решетка становится несинусоидальной. При этом амплитуды первых гармоник нелинейно зависят от интенсивности излучения. Полученные результаты актуальны для динамической голографии дисперсных жидкофазных сред, а также для оптической диагностики таких сред (например, для термооптической спектроскопии) [6–8].
Рецензенты:
Крылов В.И., д.ф.-м.н., профессор кафедры «Физика», ФГБОУ ВПО Дальневосточный государственный гуманитарный университет, г. Хабаровск;
Жуков Е.А., д.ф.-м.н., профессор кафедры «Электроника и электротехника», ФГБОУ ВПО Тихоокеанский государственный университет, г. Хабаровск.
Работа поступила в редакцию 04.09.2014.
Библиографическая ссылка
Иванова Г.Д., Кирюшина С.И., Мяготин А.В. ДИНАМИЧЕСКИЕ ГОЛОГРАММЫ В ЖИДКОФАЗНОЙ ДИСПЕРСНОЙ СРЕДЕ // Фундаментальные исследования. – 2014. – № 9-10. – С. 2164-2168;URL: https://fundamental-research.ru/ru/article/view?id=35288 (дата обращения: 25.04.2024).