Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

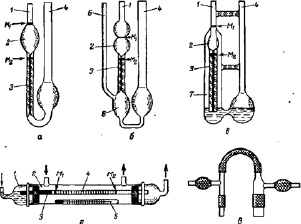
Рис. 1. Вискозиметры Оствальда (а), Уббелоде или ВПЖ-1 (б) Мартина (в). Микровискозиметр (г) и насадка Эппельбея (д)

Основная идея, лежащая в основе таких конструкций – это нестационарное течение (предположительно «ньютоновской») жидкости в сообщающихся сосудах. Она определяет все достоинства и недостатки схемы.

Подкупающая (внешняя) простота и изя щество конструкции таких вискозиметров, в особенности схемы Оствальда, вызывает желание рассмотреть расчётную схему такого прибора без ограничений, связанных с размерами трубки (уже не капиллярной, а произвольного диаметра), вязкостью и плотностью исследуемой жидкости, её количеством и качеством.

Под качеством здесь следует понимать возможность содержания в жидкости включений, способных легко «проскакивать» в просвет трубки.

В данной работе рассматриваются жидкости, ламинарное течение которых в круглой трубе, так же как в стеклянных вискозиметрах, точно или с некоторым приближением удовлетворяют уравнению Пуазейля.

Расчётная схема, в виде одинаковых сосудов 1 и 2 радиусом R, гидравлически соединённых горизонтальной трубкой 3 длиной L и радиусом r, показана на рис. 2.

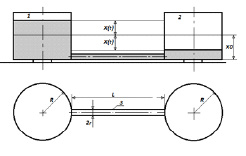
Рис. 2. Расчетная схема вискозиметра

На рис. 2 показаны: жидкость, выведенная тем или иным способом из равновесия так, что она из сосуда 1 перетекает в сосуд 2 под действием только силы тяжести; X0 – уровень, соответствующий положению равновесия жидкости в сосудах 1 и 2; X(t) – текущее отклонения уровня жидкости от положения равновесия – понижается в сосуде 1 и повышается в сосуде 2.

Масса жидкости, размещённой в сосудах 1 и 2 и трубке 3, равна

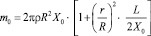, (1)

где ρ,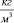 – плотность жидкости; R, м – радиус сосудов 1 и 2; r, L, м – радиус и длина трубки.

За координату, характеризующую изменения сил в системе, примем X(t) – текущее отклонение уровня жидкости в сосудах 1 и 2 от положения равновесия.

В неустановившемся движении перетекания участвует вся жидкость массы m₀.

Поэтому силу инерции, препятствующую изменению скорости восстановления равновесия жидкости, представим в виде

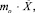Н. (2)

Сила, стремящаяся вернуть систему в состояние равновесия, равна всей неуравновешенной части жидкости в виде

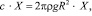Н, (3)

где g,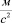 – ускорение силы тяжести.

Полагаем, что силой, препятствующей перетеканию жидкости их сосуда 1 в сосуд 2, является сила вязкого трения в трубке 3.

Для её аналитического представления рассмотрим уравнение Пуазейля

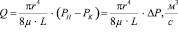, (4)

где Q,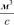 – объёмный расход жидкости c вязкостью µ, Па•с;

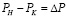, Па – перепад давлений жидкости в начале и в конце трубки.

Из физических соображений (условие неразрывности) объёмный расход жидкости через трубку 3 равен убыли её объёма во времени в сосуде 1 и соответственно увеличению объёма в сосуде 2, то есть характеризует силу вязкого трения, препятствующей перемещению неуравновешенной массы жидкости со скоростью изменения уровня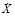 через трубку 3.

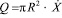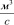,. (5)

Произведение

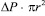, H. (6)

Из уравнения (4) с учётом (5) и (6) следует выражение для силы вязкого трения, препятствующего достижению положения равновесия в виде

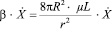, H. (7)

Таким образом, сумма выражений (2), (3) и (7) представляет собой дифференциальное уравнение свободных колебаний уровня жидкости в сообщающихся сосудах в виде

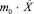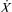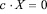+ ? +. (8)

Разделив слагаемые уравнения (8) на m0, получим дифференциальное уравнение свободных колебаний системы с одной степенью свободы в стандартном виде

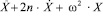= 0. (9)

Коэффициент n, характеризующий диссипативные свойства колебательной системы выражается через вышеуказанные параметры и имеет вид

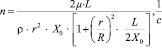. (10)

Коэффициент ω характеризует собственную частоту колебаний недемпфированной колебательной системы (µ = 0) в виде

,. (11)

В соответствии с [11], для случая 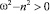и начальных условий при t = 0, X (0) = h₀ и 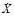(0) = 0 решение уравнения (9) имеет вид затухающих колебаний

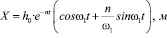, (12)

где h₀ –высота начального подъёма уровня жидкости в сосуде 1;

.

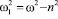Выражение для скорости изменения уровня жидкости для тех же начальных условий имеет вид

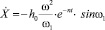. (13)

Для случая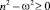 и начальных условий при t = 0, X (0) = h₀ и 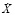(0) = 0 решение уравнения (9) имеет апериодический характер

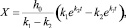(14)

где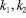 – действительные отрицательные корни характеристического уравнения, вычисляемые по формуле

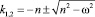. (15)

Выражение для скорости изменения уровня жидкости для тех же начальных условий в этом случае имеет вид

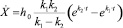. (16)

Из соотношения величин (10) и (11) может быть составлено условие, например, отсутствия периодических движений жидкости в сообщающихся сосудах в виде неравенства

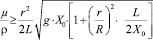. (17)

В левой части неравенства (17) отношение динамической вязкости µ к плотности ρ представляет собой кинематическую вязкость жидкости, а правая часть содержит размеры r, L, X₀, R, соответствующие рис. 2.

Полученные выше аналитические зависимости могут быть использованы при проектировании технологических установок и измерительных приборов, в которых используется принцип сообщающихся сосудов.

Эффективность применения неочевидного условия (17) можно показать на примере выбора конструктивных размеров устройства по схеме рис. 2, в которой для одной и той же жидкости при разных температурах возможны как апериодическое, так и колебательное движение.

Покажем это на примере этиленгликоля (HO-CH₂CH₂-OH), широко используемого в качестве антифриза.

На основании табличных данных, приведенных в [17], зависимость кинематической вязкости этиленгликоля от температуры показана на графике рис. 3.

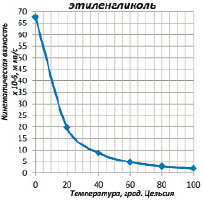
Рис. 3. Зависимость кинематической вязкости этиленгликоля от температуры

Как видно из графика на рис. 3, при увеличении температуры от 0 до + 100 °С кинематическая вязкость этиленгликоля уменьшается в 33 раза.

Выберем значения размеров, показанных на рис. 2, R = 0,02 м, r = 0,02 м, X₀ = 0,1 м, h₀ = 0,05 м, L = 0,07 м, удовлетворяющие условиям

,

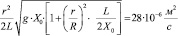и ,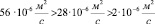

где крайние значения соответствуют кинематической вязкости этиленгликоля при + 5 °С и + 100 °С соответственно.

Для «холодного» этиленгликоля апериодический закон изменения уровня и скорости его изменения во времени показан на рисунках 4 и 5.

Для «горячего» этиленгликоля колебательный закон изменения уровня и его скорости во времени показан на рис. 6 и 7.

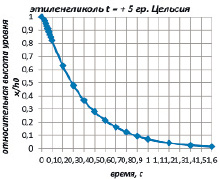
Рис. 4. График изменения уровня жидкости в сосуде во времени

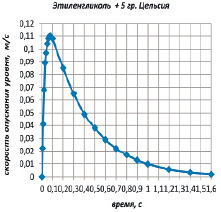
Рис. 5. График скорости изменения уровня жидкости в сосуде во времени

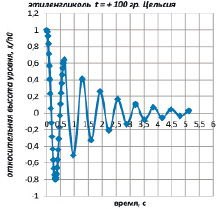
Рис. 6. График изменения уровня жидкости в сосуде во времени

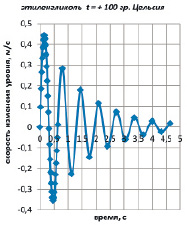
Рис. 7. График скорости изменения уровня жидкости в сосуде во времени

Полученные выше аналитические зависимости, подтвержденные опытным путем, могут быть использованы при проектировании технологических установок и измерительных приборов, в которых используется принцип сообщающихся сосудов, а рассмотренный пример с колебаниями этиленгликоля в сообщающихся сосудах представлен в учебном пособии по изучению основ гидравлики и теории колебаний для студентов, магистрантов, аспирантов и докторантов.