Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Фарахов М.М. 1 Лаптев А.Г. 2 Фарахов Т.М. 1

---

1 Инженерно-внедренческий центр «Инжехим»

2 ФГБОУ ВПО «Казанский государственный энергетический университет»

Рассмотрен подход математического моделирования в хаотичном насадочном слое при турбулентном движении газа и противоточном ламинарном волновом течении пленки жидкости. Слой насадки представляется в виде совокупности эквивалентных каналов с поправкой на извилистость. Используется идея П. Капицы о представлении волн на межфазной поверхности пленки в виде элементов шероховатости при взаимодействии с газовым потоком. Профили концентраций компонентов находятся из решения дифференциальных уравнений массопереноса, записанных для цилиндрического канала с объемным источником массы. Даны результаты решения системы уравнений и сравнение с экспериментальными данными при хемосорбции и термической деаэрации в колоннах с кольцами Рашига и насадками «Инжехим». Выполнено внедрение разработанных научно-технических решений на Казанской ТЭЦ-3.

Статья в формате PDF

1503 KB

насадка

пленки жидкости

массообмен

турбулентность

профили концентраций

1. Гольдштик М.А. Процессы переноса в зернистом слое. / М.А. Гольдштик. Новосибирск: Ин-т теплофизики СО АН СССР, 1984. – 164 с.

2. Иоффе И.И. Инженерная химия гетерогенного катализа / И.И. Иоффе, Л.М. Письмен. М.: Химия, 1965. – 352 с.

3. Каган А.М. /Контактные насадки промышленных тепломассообменных аппаратов/ А.М. Каган, А.Г. Лаптев, А.С. Пушнов, М.И. Фарахов. Монография. под ред. Лаптева А.Г. – Казань: Отечество, 2013. – 454 с.

4. Кулов Н.Н., Гордеев Л.С. Математическое моделирование в химической технолгии и биотехнологии// Теор. осн. хим. техн. – 2014. – Т.48. – №3. – С. 243–248.

5. Лаптев А.Г., Данилов В.А. Моделирование процесса хемосорбции в насадочной колонне. // Химическая промышленность. – 1998. – № 1. – С. 23–26.

6. Лаптев А.Г. Модели пограничного слоя и расчет тепломассобменных процессов / А.Г. Лаптев Казань: Изд-во Казанск. ун-та, 2007. – 500 c.

7. Лаптев А.Г., Фарахов Т.М., Дударовская О.Г. Модели турбулентной вязкости и перемешивания в каналах и насадочных проточных смесителях // Журнал Прикладной химии. – 2013. – Т. 86. № 7. – С. 1112–1121.

8. Рамм В.М. Абсорбция газов. М.: Химия, 1976. – 656 с.

9. Слеттери Дж. Теория переноса импульса, энергии и массы в сплошных средах/ Дж. Слеттери М.: Мир, 1978. – 420 с.

10. Шейдеггер А.Э. Физика течения через пористые среды / А.Э. Шейдеггер М.: Гостехиздат, 1960. – 265 с.

11. Шкляр Р.Л., Аксельрод Ю.В. Исследование хемосорбции в насадочной колонне // Химическая промышленность – 1972. – № 3. – С. 198.

12. Штерн П.Г., Руденчик Е.А., Турунтаев С.В. и др. Изотермическое осесимметричное течение несжимаемой жидкости в контактных аппаратах радиального типа. // Инж.-физ. журнал. – 1989. – Т. 56. № 4. С. 555.

13. Штерн П.Г. , Руденчик Е.А., Лукьяненко И.С. и др. Процессы переноса в зернистом слое // Теор. осн. хим. техн. – 1997. – Т. 31. № 4. – С. 428–433.

14. Ergun S. Fluid Flow through Packed Columns // Chem. Eng. Progr. – 1952. – V. 48. – № 42. – P. 89.

15. Vortmeyer D., Shuster J. Evalution of Steady Flow Profils in Reсtangular and Circular Packed Beds by a Varionational Method // Chem. Eng. Sci. – 1983. – V. 38. – № 10. P. 1691.

Проблема математического моделирования явлений переноса импульса, массы и энергии в массообменных аппаратах, является одной из важных проблем фундаментальной и прикладной науки [4]. Существующие в настоящее время теоретические подходы к решению этих задач почти всегда являются полуэмпирическими.

В данной статье рассматриваются процессы переноса при противотоке газа и жидкости в стационарных насадочных слоях с хаотичной засыпкой. Такие слои широко используются для проведений тепломассообменных и реакционных процессов.

Для расчета гидродинамических характеристик в насадки часто используют различные модификации уравнения Дарси [9, 10] (Reэ < 4) и уравнения Эргана [14, 15], учитывающие силы инерции и вязкости. При Reэ > 4 обычно используют уравнения Эргана, содержащие только квадратичный член [1, 12]. Зернистая среда, или насадочный слой, часто модернизируется как случайный массив ячеек идеального перемешивания с определенными связями между ними [2, 13].

Двумерная модель насадочного слоя и вариационный метод расчета полей скоростей и концентраций рассмотрен в работах [5, 6].

Роль активной поверхности в насадке рассмотрена в работе Кагана А.М., Пушнова А.С. и др. [3].

Целью исследования является получить математическую модель массопереноса в аппарате с хаотичной насадкой для решения задач модернизации действующих колонн или проектирования новых.

Материалы и методы исследования

Практически при использовании любых моделей насадочных слоев в качестве характерного размера используется эквивалентный диаметр.

Средний периметр каналов между насадочными элементами П в сечении колонны находят из предположения, что поверхность каналов в слое насадки равна произведению П на среднюю длину каналов Нк, где Н – высота слоя насадки; к – коэффициент, учитывающий извилистость каналов (к > 1). Таким образом,

SHa_v = ПНк,

где a_v – удельная поверхность насадки, м2/м3; S – площадь сечения колонны, м2.

Отсюда записывают [8] П = Sa_v/к. Эквивалентный диаметр насадки dэ определяется как эквивалентный диаметр каналов, по которым движется газ. Тогда, используя известное выражение для эквивалентного диаметра, записывают:

,

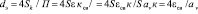где ε_св – удельный свободный объем насадки, м3/м3.

Критерий Рейнольдса для газа рассчитывают по действительной скорости газа в слое W_г: 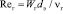; ν_г – коэффициент кинематической вязкости газа, м2/с. Началу турбулентного режима в насадке соответствует Re_г = 40–50. Полностью развитый режим наступает при Re > 2000. Дэвидсон получил коэффициент извилистости к = π/2, и поэтому можно считать, что пленочное течение в хаотичных насадках соответствует пленочному течению по вертикальной поверхности при эквивалентном критерии Рейнольдса для жидкости 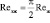, где 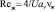; U – плотность орошения (приведенная скорость жидкости), 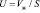, м3/ (м2·с); Vж – объемный расход жидкости, м3/с.

Представляя хаотичный насадочный слой в вертикальном направлении движения газового потока в виде совокупности параллельных эквивалентных каналов, с учетом взаимодействия фаз (стока или притока массы компонента вещества) в форме объемных источников массы, запишем систему уравнений массопереноса в эквивалентном канале в цилиндрических координатах (турбулентный режим):

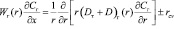, (1)

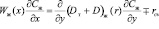, (2)

где Wг, W_ж – скорости газа и жидкости, м/с; D, D_т – коэффициенты молекулярного и турбулентного переноса массы, м2/с; Сг, С_ж – концентрация перераспределяемого компонента в газовой и жидкой фазах; r – радиальная координата, м; х – вертикальная координата, м; y – поперечная координата по нормали к поверхности пленки жидкости, м; r_cv – объемный источник массы; индексы: г – газ, ж – жидкость.

Без использования источниковых членов решение системы уравнений (1), (2) возможно с записью граничных условий четвертого рода. Однако это не учитывает характеристики насадок и дает значительные трудности при численном решении.

При ламинарном течении пленки жидкости и турбулентном режиме для газа имеем:

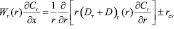, (3)

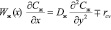. (4)

Новые конструкции нерегулярных насадок характеризуются Pe_ж > 10, где число Пекле 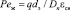; q – удельный расход жидкости, м3/(м2·с); D_п – коэффициент обратного перемешива ния, м2/с.

Известно, что если Pe_ж > 10, то можно принять модель идеального вытеснения.

Тогда для эквивалентного канала насадки уравнения массопереноса для газовой и жидкой фаз получат вид:

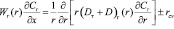, (5)

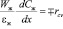, (6)

где ε_ж – удельная задержка жидкости в насадке, м3/м3.

В правой части уравнений rсv – объемный источник массы, который определяет переход массы компонента из одной фазы в другую в единице объема слоя

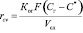, (7)

где К_ог – коэффициент массопередачи; C*– равновесная концентрация; V_сл – объем слоя 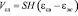; F – поверхность массопередачи, м2. Движущая сила массопередачи 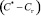записана для процесса десорбции растворенных газов или ректификации легколетучего компонента. Для абсорбции газов записывается в виде .

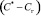Если вся поверхность насадки смочена жидкостью, то 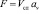, а если не вся, то используется коэффициент смачиваемости [3, 8].

Коэффициент массопередачи связан с коэффициентами массоотдачи, которые можно вычислить по выражениям математической модели [6] или для исследованных насадок по эмпирическим зависимостям [3, 8].

Для определения среднего коэффициента турбулентной диффузии в ядре потока в насадочном слое примем 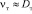, а 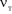найдем по формуле [7]

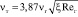, (8)

где 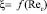коэффициент гидравлического сопротивления насадки, находится, как правило, экспериментально [3, 8].

Профиль скорости газового потока в эквивалентном канале принимается логарифмическим и имеет вид как для шероховатого канала. Это допущение основано на гипотезе П. Капицы в представлении волн при пленочном течении в виде элементов шероховатости. Тогда для второго предельного режима проявления шероховатости запишем известное выражение

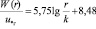, (9)

где k – высота выступов шероховатости волн, м; 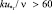; u*г – динамическая скорость на поверхности раздела фаз, м/с.

Значение u*г при противотоке пленки с газом можно вычислить из уравнения баланса сил при известном коэффициенте гидравлического сопротивления эквивалентного канала

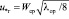, (10)

где W_ср – средняя скорость газа в канале, м/с; 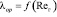– коэффициент гидравлического сопротивления [8]; .

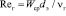Таким образом, система уравнений (5), (6) при использовании условия равновесия 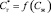, является замкнутой и при назначенных граничных условиях решается численными методами (например, методом прогонки). Результатом решения являются профили концентраций в газовой и жидкой фазах, что дает возможность вычислить эффективность массопередачи.

Результаты исследования их обсуждение

Корреляция экспериментальных данных [11] и расчетных профилей концентрации распределяемого компонента представлена на рис. 1 и 2. Исследовалась колонна с тремя секциями насадки из колец Рашига. При вычислении объемного источника массы (7) при хемосорбции учитывается ускорение массопередачи за счет химических реакций [8].

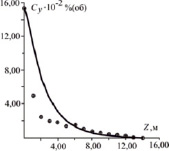
Рис. 1. Профиль концентрации Н2S в газовой фазе по высоте колонны в процессе хемосорбции в насадочном слое раствором МЭА (G = 44,46 т/ч; Lx = 36,11 т/ч; H = 3?5 м; Dк = 2 м; точки – эксперимент [11]; кривая – расчет по уравнениям модели)

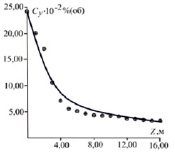
Рис. 2. Профиль концентрации СО2 в газовой фазе по высоте колонны в процессе хемосорбции в насадочном слое раствором МЭА (G = 44,46 т/ч; Lx = 36,11 т/ч; H = 3?5 м; Dк = 2 м; точки – эксперимент [11]; кривая – расчет по уравнениям модели)

На рис. 1, 2 – L,G – массовые расходы жидкости и газа, т/ч; Н – высота насадки (три секции по 5 метров); Dк – диаметр колонны, м.

Как видно из рис. 1 и 2, математическая модель удовлетворительно описывает профиль концентрации компонента по высоте колонны. Следует отметить, что решение системы уравнений (5), (6) дает близкие результаты c решением полной системы уравнений движения и массопереноса для насадочной колонны [5, 6]. Однако решение уравнений (5), (6) занимает меньшее вычислительное время и менее трудоемко с точки зрения выбора замыкающих соотношений.

В частном случае, если основное сопротивление массопередачи сосредоточено в жидкой фазе (например, десорбция труднорастворимых газов), то задача расчета эффективности значительно упрощается и решение уравнения (6) имеет вид

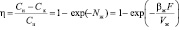, (11)

где N – число единиц переноса; β_ж – коэффициент массоотдачи в жидкой фазе, который в данном случае будет равен коэффициенту массопередачи, м/с; F – поверхность контакта фаз, м2; V_ж – объемный расход жидкости, м3/с; Сн, Ск – начальная и конечная концентрация компонента в жидкой фазе.

С использованием представленной математической модели выполнены расчеты термического деаэратора (удаление растворенного кислорода из воды) для Казанской ТЭЦ-3. На основе расчетов разработаны технические решения по модернизации колонки деаэратора ДСА-300 с использованием нерегулярной насадки «Инжехим-2000» [3]. Расчетные профили концентрации кислорода в воде даны на рис. 3. Требуемое содержание кислорода в воде менее 30 мкг/дм3.

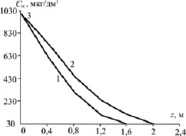
Рис. 3. Распределение поля концентраций кислорода в жидкой фазе по высоте колонны. Деаэрация воды: 1 – насадка «Инжехим-2000» размером 45 мм, 2 – насадка «Инжехим-2000» размером 60 мм. Расход воды 300 т/ч, пара – 10 т/ч

На основе моделирования и проведенных расчетов массообменных процессов, предложена следующая схема модернизации деаэратора ДСА-300 (рис. 4).

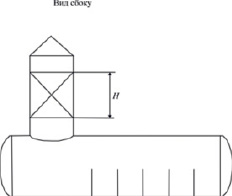
Рис. 4. Схема модернизации деаэратора ДСА-300, H – высота слоя насадки

Устаревшие струйные контактные устройства заменяются на слой неупорядоченной насадки «Инжехим-2000» с номинальным размером 60 мм. В колонке деаэратора можно разместить слой высотой около 1,6 м. Диаметр колонки 2 м.

Сотрудниками ИВЦ «Инжехим» совместно с Казанской ТЭЦ-3 выполнена модернизация одного деаэратора. Эксплуатация показала повышение эффективности удаления кислорода из воды в 3–4 раза, и превышение нормы не наблюдается.

Таким образом, выполненная модернизация подтвердила правильность расчетов по математической модели и высокую эффективность насадки «Инжехим».

Выводы

В данной статье на основе математических следствий законов сохранения импульса и массы компонента в двухфазной среде (газ–жидкость) получена математическая модель массопереноса для хаотичного слоя в аппарате. Система уравнений решается численно и показано удовлетворительное согласование с экспериментальными данными по профилю концентраций по высоте слоя. Выполнены расчеты и разработаны технические решения по модернизации термического деаэратора, внедренные на Казанской ТЭЦ-3.

Математическая модель может использоваться для расчета эффективности насадочных колонн в различных отраслях промышленности.

Статья выполнена в рамках проектной части государственного задания в сфере научной деятельности. Заявка №13.405.2014/К.

Библиографическая ссылка