Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Андреева Е.А. 1 Мазурова И.С. 1

---

1 ФГБОУ ВПО «Тверской государственный университет»

Рассматривается задача оптимального управления в модели хищник ‒ жертва при наличии сосредоточенного и распределенного запаздывания. Математическая модель взаимодействия двух популяций описывается системой интегро-дифференциальных уравнений типа Вольтерра. Для исходной непрерывной задачи сформулирован принцип максимума с учетом заданных ограничений и вида функционала. Разработан численный метод построения приближенного оптимального управления на основе метода быстрого автоматического дифференцирования. Показано, что полученное численным методом приближенное оптимальное управление с заданной точностью удовлетворяет принципу максимума для исходной непрерывной задачи. Показано, что наличие распределенного запаздывания в системе приводит к периодическим решениям, при увеличении запаздывания увеличивается амплитуда колебаний и значение минимизируемого функционала. Оптимальное решение построено при различных параметрах задачи и видах минимизируемого функционала. Исследовано влияние штрафных коэффициентов на оптимальное решение.

Статья в формате PDF

794 KB

оптимальное управление

интегро-дифференциальные уравнения

модель хищник ‒ жертва

метод быстрого автоматического дифференцирования

1. Андреева Е.А., Цирулева В.М. Вариационное исчисление и методы оптимизации. – М.: Высшая школа, 2006.

2. Андреева Е.А., Дждеед М. Оптимальное управление системами, описываемыми интегральными и интегродифференциальными уравнениями. – Тверь, 2003.

3. Андреева Е.А., Евтушенко Ю.Г. Численные методы решения задач оптимального управления для систем, описываемых интегро-дифференциальными уравнениями типа Фредгольма // Модели и методы оптимизации. – 1989. – № 1. – С. 4–13.

4. Евтушенко Ю. Г. Методы решения экстремальных задач и их применение в системах оптимизации. – М.: Наука. – 432 с.

5. Евтушенко Ю.Г. Оптимизация и быстрое автоматическое дифференцирование // Научное издание ВЦ РАН. – 2013. – 144 с.

6. Andreeva E.A., Mazurova I.S. Optimal control of predator-prey model with distributed delay // Mathematical Modelling and Geometry (Электронный ресурс). – 2013. – Vol. 1, № 3. –Р. 38–48 – Режим доступа: http://mmg.tversu.ru

Математические модели, описываемые интегро-дифференциальными уравнениями, возникают при исследовании экологических, физических, экономических процессов [1, 2]. Эти модели являются неавтономными, поэтому важным вопросом является исследование периодических решений, их устойчивости и управляемости, построение оптимального управления и разработка численных методов построения приближенного оптимального решения для систем, описываемых интегро-дифференциальными уравнениями, или систем с распределенным запаздыванием.

В моделях взаимодействия популяций типа хищник жертва периодические решения могут возникать в связи с периодичностью функций, участвующих в описании процессов их зависимости от сезонов года, погоды, доступности пищи, охоты или сбора урожая.

Ранее в работе [2] рассматривалась задача управления динамической системой, описываемой интегро-дифференциальными уравнениями с сосредоточенным и распределенным запаздыванием, в которой требуется найти оптимальное управление, минимизирующее заданный критерий

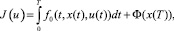(1)

при этом управляемый процесс описывается системой интегро-дифференциальных уравнений типа Вольтерра

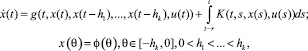(2)

а оптимальное управление удовлетворяет заданному ограничению

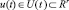п.в. t ∈ [0, T] = Γ,

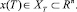(3)

Пусть далее x₁(t) и x₂(t) – численность популяций жертв и хищников соответственно в момент времени t. Математическая модель взаимодействия двух популяций описывается системой интегро-дифференциальных уравнений

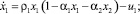
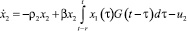(4)

при заданных начальных условиях

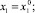
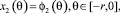(5)

где ρ₁ и ρ₂ – величины, характеризующие скорость роста численности жертв и скорость убыли численности хищников; αi, i = 1, 2 – соревновательный фактор; G(t – τ) – плотность распределения популяции x1(t). Функции управления u_i(t) – скорость отлова популяции, удовлетворяет ограничениям 0 ≤ u_i(t) ≤ b_i, i = 1, 2, t ∈ [0, T].

Задача оптимального управления заключается в минимизации функционала

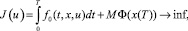(6)

где функции – f₀(t, x, u) – прибыль от реализации популяции, а слагаемое Φ(x(T)) отвечает за сохранность популяций.

Согласно [2] оптимальное управление удовлетворяет принципу максимума

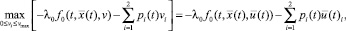(7)

а сопряженные функции pi(t) являются решением системы интегро-дифференциальных уравнений

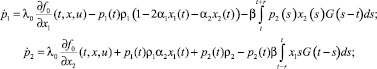(8)

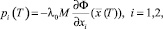pi(t) º 0 при t > T. (9)

Заметим, что если 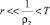, то справедлива следующая оценка

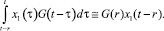
В этом случае система (4)–(5) представляет собой систему дифференциальных уравнений с сосредоточенным запаздыванием

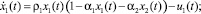
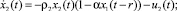
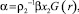(10)

где xi(t) = φi(t), t ∈ [–r, 0].

В этом случае оптимальное управление удовлетворяет условию (7), а сопряженные функции p_i(t), i = 1, 2 являются решением системы c отклоняющимся аргументом

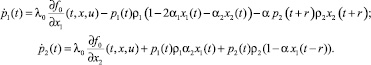(11)

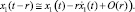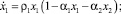
При малых значениях параметра запаздывания r справедлива оценка Система дифференциальных уравнений с запаздыванием сводится к системе обыкновенных дифференциальных уравнений 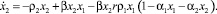(12)

(12)

Ненулевое положение равновесия системы (12) существует, если β > ρ₂α₁, и определяется из условий

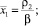
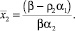
Для решения задачи оптимального управления (4)–(6) в работе используется метод быстрого автоматического дифференцирования (БАД), разработанный в ВЦ РАН под руководством Ю.Г. Евтушенко [5]. Метод БАД позволяет с единых позиций определять градиенты для явно и неявно определенных функций и для вычислительных процессов, которые являются результатом дискретизации непрерывных систем, описываемых дифференциальными и интегро-дифференциальными уравнениями. На основе метода БАД разработан комплекс программ построения приближенного оптимального управления для задачи (4)–(6) и проведен численный эксперимент, результаты которого представлены ниже. В качестве критерия остановки алгоритма в работе применяются следующие условия:

1.

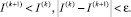
2.

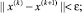
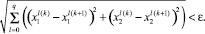
3.

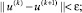
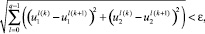
где I^(k) , x^(k) , u^(k) – значение минимизируемой функции, функции состояния и функции управления на k итерации соответственно.

Построим оптимальное решение задачи (4)–(6) с учетом распределенного запаздывания, в которой целью является минимизация функционала

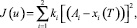
отвечающего за сохранность популяции на заданном уровне в конечный момент времени.

Ниже, на рис. 1–2, представлены графики численности популяций x_i(t), i = 1, 2 в зависимости от величины запаздывания r при следующих параметрах системы: α₁ = 0,05, α₂ = 0,05, ρ₁ = 0,75, ρ₂ = 0,75, β = 0,1, u_i(t) ≤ 0, 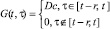, T = 45, A₁ = 7, A₂ = 13. Точность метода ε = 0,0000001.

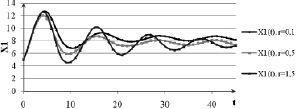
Рис. 1. Графики численности популяции жертв 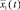для управляемой системы с распределенным запаздыванием (4)–(5) в зависимости от времени t при различных значениях запаздывания r

Соответствующие этим решениям графики функции управления в зависимости от величины запаздывания r представлены на рис. 3–4.

Легко видеть, что оптимальное управление удовлетворяет принципу максимума (7). При увеличении запаздывания увеличивается значение минимизируемого функционала, уменьшается устойчивость решения.

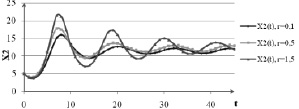
Рис. 2. Графики численности популяции хищников 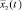для управляемой системы с распределенным запаздыванием (4)–(5) в зависимости от времени t при различных значениях запаздывания r

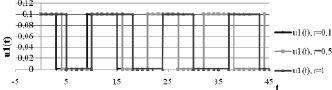
Рис. 3. Графики функции приближенного оптимального управления 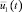для системы (4)–(5) в зависимости от времени t при различных значениях запаздывания r

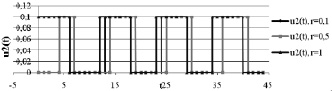
Рис. 4. Графики функции приближенного оптимального управления 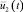для системы (4)–(5) в зависимости от времени t при различных значениях запаздывания r

Исследуем решение управляемой системы (4)–(5) с распределенным запаздыванием, целью управления которой является минимизация функционала

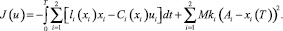(13)

Здесь первое слагаемое характеризует максимизацию прибыли, а второе – сохранение популяции в конечный момент времени на уровне x_i(T) = A_i, i = 1, 2.

Функционал (13) можно рассматривать как сумму двух взвешенных фукционалов

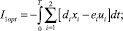
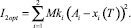
В табл. 1 представлены значения минимизируемого функционала в зависимости от значения штрафного коэффициента Mk.

Из таблицы следует, что при увеличении весового коэффициента Mk от 1 до 100 величина I_2opt/Mk уменьшается на 75 %, что соответствует более точному выполнению граничного условия

x_i(T) = A_i, i = 1, 2.

При этом величина интегрального слагаемого уменьшается на 3,5 %.

Значения минимизируемых функционалов в зависимости от значения штрафного коэффициента Mk

Таким образом, в предлагаемой работе рассмотрена задача оптимального управления для модели хищник ‒ жертва с учетом сосредоточенного и распределенного запаздывания. Сформулирован принцип максимума для исходной непрерывной задачи, разработан алгоритм построения приближенного оптимального решения, который с заданной точностью ε = 0,0000001 совпадает с теоретическими результатами. Показано, что наличие распределенного запаздывания в системе приводит к периодическим решениям, при увеличении запаздывания увеличиваются амплитуда колебаний и значение минимизируемого функционала. Оптимальное решение построено для различных типов минимизируемых функционалов. Показано, что при увеличении штрафного коэффициента перед терминальным слагаемым значение терминального слагаемого уменьшается, что соответствует более точному выполнению условия сохранения численности популяции на заданном уровне за счет уменьшения прибыли от реализации продукции.

Рецензенты:

Болодурина И.П., д.т.н., профессор, заведующий кафедрой прикладной математики, ФГБОУ ВПО «Оренбургский государственный университет», г. Оренбург;

Попов В.Н., д.ф.-м.н., доцент, заведующий кафедрой математики Института математики, информационных и космических технологий, САФУ им. М.В. Ломоносова, г Архангельск;

Бичурин М.И., д.ф.-м.н., профессор, заведующий кафедрой ПТРА, Новгородский государственный университет, г. Нижний Новгород.

Работа поступила в редакцию 23.07.2014

Библиографическая ссылка