Несмотря на наличие большого числа методов для биометрической идентификации личности, использование для этой цели подписи находит самое широкое применение. В этой связи понятен интерес исследователей к задаче автоматической идентификации личности по подписи. Первоначально подпись рассматривалась как графический объект, но с появлением новых устройств ввода возникла задача идентификации on-line подписи, то есть подписи вместе с динамикой ее создания [2, 3].
Традиционный способ идентификации объекта сводится к вычислению некоторых векторов-признаков и дальнейшему сравнению полученных векторов с помощью какой-либо метрики. В данной работе предложен новый метод получения таких векторов и представлены результаты экспериментов.
Новизна предлагаемого метода идентификации
Основой любого алгоритма распознавания является выбор признаков, представленных в виде векторов. Для дальнейшего анализа полученных векторов применяют один из возможных способов классификации. Наибольшее распространение получили методы на основе нейронных сетей или SVM [1]. Однако задача распознавания не имеет единственного решения. Предложенный способ получения векторов-признаков не отрицает имеющиеся методы распознавания, он является дополнительной альтернативой при определении результатов и заключении выводов.
Новизна предлагаемого метода заключается в том, что:
1) предлагается заменить подпись некоторой функцией от одного аргумента, причем вид этой функции не зависит от положения подписи на странице. После этого к полученной функции можно применить стандартные методы исследования;
2) в качестве снимаемых параметров используется решение системы уравнений, дающее коэффициенты представления функции подписи через радиальный базис.
Представление on-line подписи в виде функции
Переход от самой подписи к ее характеристике должен сохранять ее свойства, но не зависеть от положения подписи и ее ориентации.
On-line подпись представляется в виде текстового файла, каждая запись которого есть вектор pk = (xk, yk), заданный координатами очередной точки (сила нажима не учитывалась). Поскольку положение очередной точки определялось через равные интервалы времени, в указанном описании учитывалась динамика подписи.
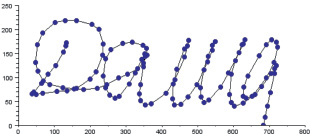
Рис. 1. Изображение подписи
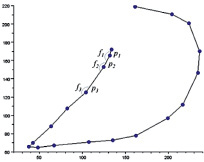
Файл подписи преобразовывается в значения функции f(t) по следующему правилу: строится последовательность чисел tk, k = 0,1,…, где t0 = 0, а tk = |pk + 1 – pk|, k > 0. Далее, f0 = 0, fk = f(tk) – угол между векторами pk и pk + 1 (рис. 2).
а
б
Рис. 2. Представление подписи в виде функции: а – фрагмент подписи; б – функция подписи
Подписи одного и того же человека не являются совершенно идентичными. В частности, построенные функции будут иметь разные области определения. Чтобы получить возможность в дальнейшем сравнивать такие функции, функции подписи нормализуют. Для этого область определения разбивается на одно и то же число (N) точек: x1, x2, x3, …, xN, равноудаленных друг от друга, а значения функции в этих точках находятся с помощью сплайн-интерполяции.
Применение радиальных функций и вейвлетов для описания подписи
Формально полученные значения функций можно использовать для описания подписи, однако индивидуальность проявляется в зависимости от значений этих функций в разных точках. С этой целью для отыскания такой зависимости был использован подход, представленный в [5]. Этот подход основывается на применении радиальных функций и вейвлетов к исследованию функции подписи.
Радиальная функция – это функция r(x), зависящая только от расстояния между x и фиксированной точкой пространства X.
Аппроксимация радиальной базисной функцией имеет вид
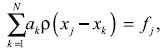(1)
где xj – xk – евклидово расстояние между узлами xj и xk; ρ(xj – xk ) – функция, зависящая только от расстояния до соответствующего узла xk и поэтому называемая радиалом; ak – весовые коэффициенты; fj = f(xj) – значение функции (величина угла) в точке xj.
Видим, что (1) представляет собой свёртку вейвлет-функции r(x) (в качестве вейвлет-функции взята радиальная функция) с сигналом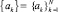 
, а значит это дискретное вейвлет-преобразование. Оно переводит исходную функцию в форму, которая делает некоторые ее величины более поддающимися изучению, позволяет получить высокое соотношение сжатия в сочетании с хорошим качеством восстановленного сигнала [4].
Возьмём каждый экземпляр подписи, построим и решим для него систему линейных уравнений:
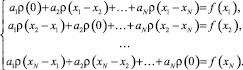(2)
В качестве r(x) согласно [5] возьмём симметричную (радиальную) центральную базисную функцию
ρ(x) = |x|α, (3)
где 0 < α < 1.
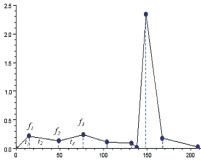
Из каждой системы уравнений определим коэффициенты {ak} разложения через радиальный базис и построим их графики (рис. 3):
Видим, что на графиках 
экземпляров подписи одного и того же автора наблюдается определённая закономерность и устойчивость значений в некоторых точках.
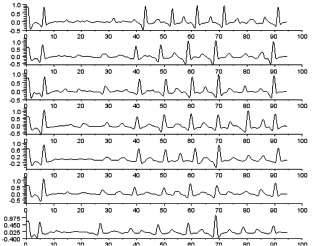
Рис. 3. Графики коэффициентов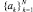 
при 0 < a < 1 (a = 0,3)
Введём метрику для коэффициентов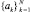 
. Для этого первоначально определим средние значения 
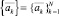для всех экземпляров подписи автора. Далее вычислим расстояния от «усреднённого» вектора 
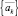подписей автора до вектора коэффициентов {ak} всех экземпляров подписей (его и остальных участников).
В ходе исследования выяснилось, что, расстояние между векторами подписей, выполненных разными людьми, превышает расстояние между векторами подписей одного автора. Этот факт открывает возможность для идентификации подписей путём применения вейвлет-преобразований и радиального базиса и дальнейшим сравнением их с учётом вводимой метрики. Можно ввести определённый порог при сравнении расстояний между векторами подписей. Если расстояние между векторами подписей A и В будет ниже порога, то принимается решение об идентичности подписей А и В, если же расстояние между векторами подписей A и В будет выше порога, то считается, что они принадлежат разным авторам.
Результаты эксперимента
Эксперимент по идентификации подписи с помощью радиального базиса проводился на 20 участниках. Для каждого участника эксперимента было использовано для исследования по 6–7 экземпляров подписей.
Рассмотрим процесс идентификации одного из участников эксперимента. Вычислим расстояния между усредненным вектором коэффициентов 
его подписи и векторами коэффициентов остальных подписей. Получим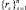 
– вектор расстояний, где n – общее число подписей всех участников. Определим минимальное rmin и максимальное rmax значения элементов вектора 
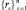. Разобьём отрезок [rmin; rmax] на М равных частей с шагом 
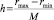– получим вектор 
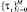, где τ0 = rmin, τM = rmax, τi+1 = τi + h. Для каждого значения порога τi, 0 ≤ i ≤ M:
1) определяем подписи, для которых соответствующее значение расстояния меньше τi, и проверяем, действительно ли это подписи автора. Определяем значение чувствительности (sensitivity) – отношение количества верно классифицированных подписей автора к общему количеству подписей автора;
2) определяем подписи, для которых соответствующее значение расстояния rs больше τi, и проверяем, действительно ли это подписи, не принадлежащие автору. Определяем значение специфичности (specificity) – отношение количества верно классифицированных подписей, не принадлежащих автору, к общему количеству подписей остальных участников.
Таким образом, формируем ROC-кривую: определяем вектор чувствительности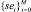 
и вектор специфичности 
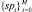, по оси Y откладываем значения 
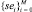, по оси X: 
.
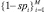При построении ROC-кривой имеется параметр (порог), варьируя который, будем получать то или иное разбиение на два класса. В зависимости от него будут получаться разные величины ошибок I и II рода. Ошибка I рода – вероятность принять подпись автора за фальшивую. Ошибка II рода – вероятность принять ложную подпись за подпись автора.
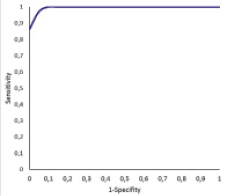
Рис. 4. ROC-кривая одного из участников эксперимента
Значение порога для принятия решения найдем исходя из баланса между чувствительностью и специфичностью. Величина порога определяется индивидуально для каждого участника эксперимента.
В результате проведенного эксперимента средняя величина ошибки первого рода составила 4,2 %, ошибки второго рода ‒ 2,3 %.
Выводы
1. Проведён анализ подписи как биометрической характеристики с учётом динамики. Применение в качестве вейвлетов радиальных функций позволило определить закономерности функций подписи среди экземпляров подписей каждого автора при разложении их через радиальный базис.
2. Новизна предлагаемого метода:
- подпись представляется в виде функции одного аргумента инвариантно относительно положения на странице;
- в качестве снимаемых параметров используется решение системы уравнений, дающее коэффициенты {ak} представления функции подписи через радиальный базис.
3. Расстояние, вычисленное между векторами коэффициентов {ak} подписей разных авторов, превышает расстояние между векторами коэффициентов подписей одного автора, что открывает возможности для идентификации подписей. Для представления результатов идентификации для каждого участника эксперимента построены ROC-кривые.
4. Предложенный способ не отрицает имеющиеся методы идентификации, он является дополнительной альтернативой при определении результатов распознавания подписи.
Рецензенты:
Песошин В.А., д.т.н., профессор, зав. кафедрой КС, КНИТУ – КАИ, г. Казань;
Шарнин Л.М., д.т.н., профессор, зав. кафедрой АСОИУ, КНИТУ – КАИ, г. Казань.
Работа поступила в редакцию 23.07.2014.
Библиографическая ссылка
Анисимова Э.С. ИДЕНТИФИКАЦИЯ ПОДПИСИ С ИСПОЛЬЗОВАНИЕМ РАДИАЛЬНОГО БАЗИСА // Фундаментальные исследования. – 2014. – № 9-6. – С. 1185-1189;URL: https://fundamental-research.ru/ru/article/view?id=35035 (дата обращения: 19.04.2024).