В работе исходя из представления о роли мягкой моды ωM(T) в сегнетоэлектрическом фазовом переходе проведены расчеты и дана интерпретация аномального поведения коэффициентов теплопроводности и теплового расширения около температуры фазового перехода ТС сегнетокерамики на основе ЦТС. Сегнетокерамики на основе твердых растворов Pb(Ti,Zr)O3 (ЦТС) со структурой типа перовскита обладают уникальными физическими свойствами и благодаря возможности их варьирования за счет изменения химического состава находят широкое применение в технике. К тому же рассматриваемая пьезокерамика относится к важному классу сегнеэлектрических систем с разупорядоченными структурами, в которых могут реализоваться размытые фазовые переходы. Механизмы таких переходов в неоднородных и многокомпонентных системах являются сложными и недостаточно выясненными, что приводит к значительным трудностям при их описании. Недавно в [1, 2] были получены новые экспериментальные данные по теплофизическим свойствам пьезокерамики на основе твердых растворов ЦТС (ПКР-8 и ПРК-7М) в области температур 300–800 К и было обнаружено аномальное поведение коэффициентов теплопроводности λ и теплового расширения α около сегнетоэлектрического фазового перехода при температуре ТС равной 600 и 460К для систем ПКР-8 и ПРК-7М соответственно.
В данном сообщении, с учетом представления о мягкой моде ωM(T) [3–9], предложена микроскопическая модель температурного поведения коэффициентов теплопроводности и теплового расширения в широкой области температур от 0 до 900 К. Для сегнетокерамики ПКР-8 расчеты согласуются с данными опытов. Несмотря на ряд использованных приближений данные расчетов качественно и количественно согласуются с экспериментом и с единых позиций мягкой моды объясняют аномальное поведение λ(T) и α(T) около ТС = 600 K для ПКР-8.
Коэффициент теплопроводности λ(T) ЦТС
Как видно из рис. 1, 2, 3, данные опытов показывают, что изменение теплопроводности с температурой имеет характер, свойственный для неупорядоченных и стеклообразных веществ, т.е. λ(T) растет с увеличением температуры. При этом в точке T = TC на кривой λ(T) наблюдается резкий излом, хотя в этой точке часто наблюдается особенность типа капса. Согласно [8–11] аномальное поведение λ(T) около TC обусловлено взаимодействием продольных акустических фононов с мягкой модой 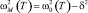 , ответственной за фазовый переход при T = TC и способной привести к заметному уменьшению теплопроводности около TC, как при температурах меньших, так и при T >TC. На поведение λ(T) в ЦТС влияет и скачок удельной теплоемкости ΔC(T), связанный с тепловыми флуктуациями около TC. Тогда коэффициент теплопроводности λ(T) для сегнетокерамики на основе ЦТС в модели Дебая можно представить в виде [3]
, ответственной за фазовый переход при T = TC и способной привести к заметному уменьшению теплопроводности около TC, как при температурах меньших, так и при T >TC. На поведение λ(T) в ЦТС влияет и скачок удельной теплоемкости ΔC(T), связанный с тепловыми флуктуациями около TC. Тогда коэффициент теплопроводности λ(T) для сегнетокерамики на основе ЦТС в модели Дебая можно представить в виде [3]
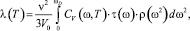 (1)
(1)
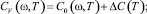 (2)
(2)
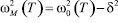
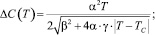 (3)
(3)
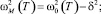
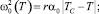
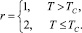 (4)
(4)
Здесь C0(ω, T) – удельная теплоемкость для фононов с частотой ω; ΔC(T) – скачкообразное изменение теплоемкости за счет тепловых флуктуаций около температуры фазового перехода второго рода, близкого к трикритической точке Тс, α, β, γ – коэффициенты соответствующего разложения термодинамического потенциала в теории Ландау; v – средняя групповая скорость фононов; V0 – молярный объем; k – постоянная Больцмана. Расчеты по формулам (1)–(4) дают неплохое качественное и количественное согласие с данными опытов (рис. 1).
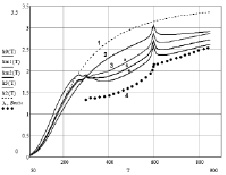
Рис. 1. Теплопроводность λ(Т) сегнетокерамики на основе твердых растворов ЦТС (цирконата-титаната свинца Pb(Ti,Zr)O3): 1 – расчет для кристаллов без вклада от процессов переброса (τu = 0) и аномальной теплоемкости при фазовом переходе и λ0 = (2,6/1,8)·1013 (моль/м·с2); 2 – для поликристалла ЦТС со вкладом в λ(Т) от аномальной теплоемкости около Тс = 600 К; 3 – для сегнетокерамики ЦТС с резонансным рассеянием фононов на двухуровневых кластерах с учетом γm(x): а – с локальной плотностью ρm(x) двухуровневых состояниий x2Im γ(x); б – с плотностью состояний xIm g(x); в – с плотностью состояний Im g(x); 4 – точки – эксперимент [1, 2]
Модели для описания поведения коэффициента теплового расширения и λ(Т)
В области размытого фазового перехода в ЦТС наблюдается резкое изменение коэффициента теплового расширения (КТР). В области около TC КТР становится отрицательным с наименьшим значением при T = TC для ПКТ-8 порядка –1,1·10–6/K. С термодинамической точки зрения отрицательное значение КТР можно объяснить отрицательными значениями эффективного коэффициента Грюнайзена [4]. В целом поведение КТР α(Т) около TC явно соответствует поведению мягкой моды 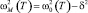 [3–5] (δ2 – ангармоническая добавка для необращающейся при T = TC в нуль мягкой моды [3]). Отрицательные значения КТР около TC при этом можно связать с неполным смягчением мягкой моды (4) за счет δ2 и мнимостью ее значений в узкой области температур ΔT = T2 – T1 = 17 K, где
[3–5] (δ2 – ангармоническая добавка для необращающейся при T = TC в нуль мягкой моды [3]). Отрицательные значения КТР около TC при этом можно связать с неполным смягчением мягкой моды (4) за счет δ2 и мнимостью ее значений в узкой области температур ΔT = T2 – T1 = 17 K, где 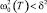 . Для описания поведения КТР и λ(Т) твердых тел около TC существует несколько разных теоретических подходов – моделей [4, 8, 9].
. Для описания поведения КТР и λ(Т) твердых тел около TC существует несколько разных теоретических подходов – моделей [4, 8, 9].
В частности, около температуры TC сегнетоэлектрического фазового перехода, как правило, на кривой теплопроводности λ(Т) наблюдаются типичные особенности различного вида [8, 9]:
а) излом или особенность типа капса (скобки), направленные в «отрицательную» сторону, т.е. в сторону уменьшения значений λ(Т);
б) явно выраженный в широкой области температур отрицательный минимум и относительно узкий (в виде провала), направленный вниз «пик»;
в аномалия типа «ступеньки» или шаг – точка разрыва первого рода;
г) положительный, почти симметричный, мало выраженный пик на фоне широкой области уменьшения значений теплопроводности λ(Т);
д) разрыв или точка разрыва второго рода при T → TC.
Такие особенности обусловлены критическим рассеянием акустических фононов на колебаниях мягкой моды и на «центральном пике». Это рассеяние и ведет к аномальному поведению λ(Т) при T → TC [8–11].
Расчет КТР в сегнетокерамике ЦТС
С учетом наличия в ЦТС сегнетоэлектрического фазового перехода с мягкой модой ωM(T) для описания поведения КТР в ЦТС воспользуемся моделью мягкой моды (4). Тогда для α(Т) получаем:
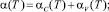
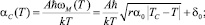 (5)
(5)
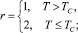
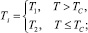 (6)
(6)
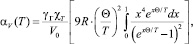 (7)
(7)
где R – постоянная уравнения состояния системы; δ0 – отрицательное значение КТР в области мнимой частоты ωM(T). Расчеты по формулам (5)–(7) дают хорошее качественное и количественное согласие с данными опытов (рис. 2 и 3). В расчете были использованы следующие значения параметров теории:
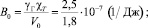
v = 104 (м/с); V0 = 6·10–6 (м3/моль);
δ0 = 3·10–6 (1/К); T1 = 586 K, T2 = 603 K.
На рис. 3 представлено сопоставление результатов вычислений λ(T) и α(Т) с данными эксперимента [1, 2], при этом кривая 1 для λ(T) получена в предположении асимметричного поведения скачка теплоемкости ΔC(T) около TC, т.е. при T > TC в соответствии с данными опытов были использованы значения ΔC(T) = C0T, где C0 = 5·10–3 Дж/с·м·К. Заметное (до 30–40 %) превышение при T < 400 K рассчитанных значений λ(T) над данными опытов, видимо, связано с необходимостью более точного определения плотности состояний ρm(x), при больших значениях концентрации двухуровневых систем.
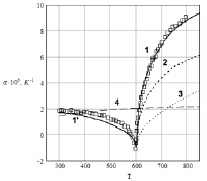
Рис. 2. Коэффициент теплового расширения сегнетокерамики ПКР-8. Результаты расчетов: кривые 1′, 3 с параметрами: α0 = 1,32 (мэВ2/К), A0 = (1,602/1,38)·10–7, при T < TC и T ≥ TC соответственно; кривые: 2 – A0 = 0,7·(1,602/1,38)·10–7; 1 – A0 = (1,602/1,38)·10–4 (1/мэВ), 4 – вклад в КТР от αV(T); точки – эксперимент [1, 2]
Как видно на рис. 3, результаты расчетов по предложенным выше моделям (1), (5) для λ(Т) и для α(Т) с учетом мягкой моды объясняют температурное поведение коэффициентов теплопроводности и теплового расширения ЦТС и хорошо согласуются с данными опытов.
Обсуждение
Рассмотренные выше особенности, как правило, обусловлены критическим рассеянием акустических фононов на колебаниях мягкой моды и на «центральном пике». Это рассеяние ведет к аномальному поведению λ(Т) при T → TC [8–11]. На кривой λ(Т) в ЦТС в точке TC, однако, наблюдается нетипичный (положительный) излом, направленный в сторону увеличения значений λ(Т). По-видимому, это характерно для сильно неупорядоченных, стеклообразных и сегнетокерамических систем с размытыми фазовыми переходами. При таком поведении кривой λ(Т) естественно предположить, что в ЦТС важную роль играет скачок удельной теплоемкости ΔC(T), обусловленный тепловыми флуктуациями около TC. В такой ситуации времена релаксации фононов (τ0(ω), τc(ω)) осредняются согласно [7] и ведущим механизмом теплового сопротивления остается характерное для стекол резонансное рассеяние фононов на двухуровневых системах γm(x). При этом помимо аномалии на кривой λ(Т) около TC в расчете может появиться максимум (рис. 1) при температуре порядка 250 К. Поэтому представляли бы значительный интерес экспериментальные данные по теплопроводности λ(Т), теплоемкости C(T) и КТР α(Т) ЦТС в более широкой области температур (50–1000 К).
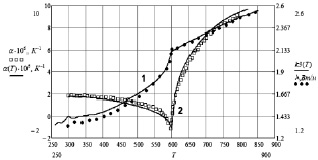
Рис. 3. Температурная зависимость коэффициентов теплопроводности и теплового расширения сегнетокерамики ЦТС (ПКР-8): кривая 1 – расчет λ(Т) с учетом скачка теплоемкости при T = TC (A = 1,22·106, ρm(x) = xIm g(x)); кривая 2 – расчет аномального поведения a(Т), обусловленного мягкой модой 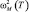 ; точки и ромбики – данные экспериментов [1] и [2]
; точки и ромбики – данные экспериментов [1] и [2]
Согласно [4] отрицательная область значений коэффициента теплового расширения (КТР) в твердых телах может иметь весьма разную природу и разную форму, например, как в ПКР-7М [1, 2]. Это обстоятельство интерпретируется исходя из самых разных подходов [4]. В нашей модели при 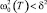 имеем мнимые значения мягкой моды
имеем мнимые значения мягкой моды 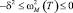
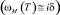 , что соответствует согласно (5) отрицательным значениям КТР с δ0 = –3·10–6 (1/K) в области T1 ≤ T ≤ T2.
, что соответствует согласно (5) отрицательным значениям КТР с δ0 = –3·10–6 (1/K) в области T1 ≤ T ≤ T2.
Остается неясным наблюдаемое слишком резкое возрастание α(Т) справа от TC (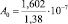 , при T < TC и
, при T < TC и 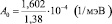 , при T ≥ TC, рис. 2). Отметим, что еще более значительное возрастание α(Т) при T ≥ TC наблюдается для ряда систем, в том числе в кристаллах триглицинсульфата (ТГС). Несмотря на это предложенные нами в работе модели для λ(Т) и для α(Т) с единых позиций мягкой моды хорошо качественно объясняют температурное поведение коэффициентов теплопроводности и теплового расширения ЦТС и результаты расчетов количественно согласуются с данными опытов.
, при T ≥ TC, рис. 2). Отметим, что еще более значительное возрастание α(Т) при T ≥ TC наблюдается для ряда систем, в том числе в кристаллах триглицинсульфата (ТГС). Несмотря на это предложенные нами в работе модели для λ(Т) и для α(Т) с единых позиций мягкой моды хорошо качественно объясняют температурное поведение коэффициентов теплопроводности и теплового расширения ЦТС и результаты расчетов количественно согласуются с данными опытов.
Рецензенты:
Янукян Э.Г., д.ф.-м.н., профессор, декан инженерного факультета профессор кафедры физико-математических дисциплин, филиал СКФУ, г. Пятигорск;
Чернобабов А.И., д.ф.-м.н., профессор кафедры физико-математических дисциплин, филиал СКФУ, г. Пятигорск.
Работа поступила в редакцию 15.07.2014.
Библиографическая ссылка
Алтухов В.И., Казаров Б.А., Касьяненко И.С., Санкин А.В., Филипова С.В. РАСЧЕТ АНОМАЛЬНОГО ПОВЕДЕНИЯ КОЭФФИЦИЕНТОВ ТЕПЛОПРОВОДНОСТИ И ТЕПЛОВОГО РАСШИРЕНИЯ СЕГНЕТОКЕРАМИКИ НА ОСНОВЕ ТВЕРДЫХ РАСТВОРОВ ЦИРКОНАТА-ТИТАНАТА СВИНЦА // Фундаментальные исследования. 2014. № 9-5. С. 1008-1012;URL: https://fundamental-research.ru/ru/article/view?id=35006 (дата обращения: 14.01.2026).



