Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Волков М.В. 1 Королев Л.В. 1 Таршис М.Ю. 1

---

1 ФГБОУ ВПО «Ярославский государственный технический университет»

Предложена математическая модель процесса смешивания сыпучих материалов в устройстве гравитационно-пересыпного действия. В основе модели лежит закон сохранения массы ключевого компонента в микрообъеме смеси. При этом поток ключевого компонента складывается из двух составляющих: потока циркуляции, отображающего движение частиц материала по замкнутым траекториям, и потока сегрегации, возникающего вследствие различия частиц по физическим свойствам. Скорость потока сегрегации определяется локальной концентрацией ключевого компонента и отношением плотностей и размеров частиц ключевого и несущего компонентов. В модели учитывается влияние на процесс смешивания дополнительных рабочих органов, лопаток, установленных в смесителе, которые препятствуют развитию потока сегрегации. Результаты численных расчетов, проведенных по данной модели, удовлетворительно согласуются с имеющимися экспериментальными данными, что дает возможность использовать ее для инженерного расчета смесителей гравитационно-пересыпного действия.

Статья в формате PDF

618 KB

смешивание

сыпучий материал

барабанный смеситель

сегрегация

нелинейное уравнение переноса

1. Таршис М.Ю., Королев Л.В., Зайцев А.И. Теория и принципы моделирования процесса смешивания сыпучих материалов и создания устройств с гибкими элементами для его реализации: монография. – Ярославль: изд-во ЯГТУ, 2011. – 100 с.

2. Таршис М. Ю., Зайцев А. И., Королев Л. В.,. Волков М. В Смеситель // Патент России 2466778, B01F9/06 . опубл. 20.11.12, Бюл. № 32.

3. Fan L.T., Chen Y.M.,. Lai F.S Recent developments in solid mixing // Powder Technology. – 1990. – Vol. 61. – P. 255–287.

4. Prigozhin L., Kalman H. Radial mixing and segregation of a binary mixture in a rotating drum: Model and experiment // Phys. Rev. E 57. – 1998. – Р. 2073–2080.

5. Волков М.В., Королев Л.В., Таршис М.Ю. Исследование механики движения сыпучего материала в поперечном сечении смесителя гравитационно-пересыпного действия // Фундаментальные исследования. – 2014. – № 5 (часть 4). – С. 692–696.

6. Придатко Ю.М., Королев Л.В., Готовцев В.М. Моделирование плотной упаковки частиц композитного материала // Вестник СГТУ. – 2011. – № 4(62), Вып 4. – С. 96–100.

Процессы смешивания сыпучих материалов находят широкое применение во многих отраслях современной промышленности, особенно в химической, строительной, в металлургии, сельскохозяйственном производстве и других. Достаточно хорошо зарекомендовали себя на практике смесители гравитационно-пересыпного действия (как правило, это смесители барабанного типа) благодаря своей низкой энергоемкости и простоте конструкции. Однако в большинстве случаев необходимо получение смесей из компонентов, отличающихся по своим физико-механическим свойствам (средним диаметрам частиц, их плотностям, форме и другим), а такие смеси склонны к сегрегации. В качестве одного из методов подавления сегрегации используется установка внутри рабочего объема смесителя дополнительных перемешивающих элементов. За последние годы был разработан ряд новых конструкций такого типа [1, 2], в том числе допускающих изменение расстояния рабочих элементов от оси вращения барабана [2].

Для выбора оптимальных конструкционных и режимных параметров этих смесительных устройств необходимы адекватные математические модели реализуемого в них процесса, учитывающие сегрегацию смеси. Различные подходы к моделированию процессов смешивания рассмотрены в работах [1, 3, 4] и многих других. При этом наиболее информативными и надежными подходами считаются те, которые основаны на законе сохранения массы ключевого компонента в микрообъеме сыпучей среды и потому позволяют анализировать не только интегральные характеристики смеси, такие как коэффициент неоднородности или энтропию, но и локальные концентрации ключевого компонента в каждой точке рабочего объема в произвольный момент времени. Построение таких моделей требует подробного изучения потоков материала в рабочем объеме устройства и связанных с ними механизмов пространственного перераспределения частиц различных фракций. В настоящей работе предлагается модель процесса смешивания в смесителе гравитационно-пересыпного действия [2], основанная на результатах статьи [5], где было найдено поле скоростей сыпучей массы в данном устройстве, и учитывающая эффект сегрегации, возникающий при совместном движении частиц, различающихся по физико-механическим свойствам.

Рассмотрим процесс гравитационно-пересыпного смешивания сыпучих материалов в рабочем объеме, ограниченном цилиндрической поверхностью радиуса R, движущейся с угловой скоростью ω (рис. 1). В плоском сечении (x, y) рабочего объема, перпендикулярном оси вращения, можно выделить две характерные области движения материала. В примыкающей к движущейся поверхности области транспортирования сыпучий материал перемещается без сдвига слоев и смешивания не происходит. В области активного смешивания материал скатывается вдоль линии обрушения под действием силы тяжести. При этом возникает взаимное смещение слоев частиц, которое приводит к выравниванию поля объемных концентраций ключевого компонента смеси c(x, y, t) с течением времени t. Если частицы ключевого и несущего компонентов различаются по физико-механическим свойствам, то, наряду со смешиванием, связанным с движением частиц вдоль линий тока в поле скоростей 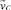, возникает переход частиц из одной линии тока в другую со скоростью 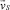, приводящий к сегрегации смеси.

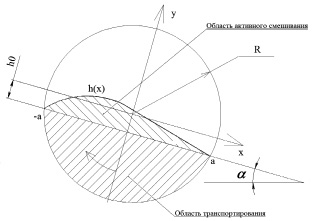
Рис. 1. Поперечное сечение рабочего объема

Изменение концентрации в рабочем объеме смеси при отсутствии входящих и исходящих внешних потоков материала в процессе смешивания и сегрегации описывается уравнением непрерывности

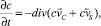(1)

которое при заданных полях скоросте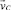й и 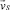и начальном распределении ключевого компонента c(x, y, t = 0) определяет c(x, y, t) в любой момент времени.

Скорость движения сыпучего материала по линиям тока 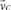была найдена в работе [5] методами механики сплошной среды в предположении, что линия обрушения (–a, a) является отрезком прямой. В области транспортирования y < – h₀

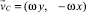, (2)

в области активного смешивания –h₀ < y < h(x)

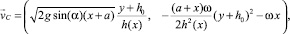(3)

где g – ускорение свободного падения; α – угол обрушения; 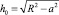 – уровень линии обрушения;  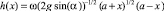– функция, определяющая форму области активного смешивания, а полудлина линии обрушения a определяется при заданном коэффициенте загрузки q из уравнения

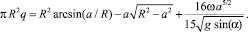
Скорость потока сегрегации 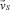отлична от нуля только в области активного смешивания и может быть определена исходя из следующих рассуждений. Будем считать, что направленный переход частицы ключевого компонента из одной линии тока в другую (в отличие от случайного, диффузионного, которым мы в данной работе пренебрегаем) возникает из-за того, что сила тяжести Fg, действующая на частицу, и архимедова сила FA, то есть сила давления на частицу со стороны примыкающих к ней частиц, перестают компенсировать друг друга. В направлении возникающей равнодействующей силы и происходит смещение частицы. Поскольку движение частицы происходит в стесненных условиях, будем полагать, что скорость смещения пропорциональна возникающей силе

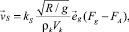(4)

где 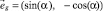 – единичный вектор направления силы тяжести; ρk и Vk – плотность и объем частицы ключевого компонента;  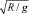– характерный масштаб времени для рассматриваемой системы; kS – безразмерный модельный коэффициент сегрегации. Выражения для сил Fg и FA можно записать в виде:

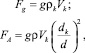(5)

где ρ и d – плотность и диаметр частиц материала, окружающего частицу ключевого компонента; d_k – диаметр частиц ключевого компонента. В формуле для F_A учтено, что давление на частицу в сыпучей среде определяется не только плотностью окружающих ее частиц ρ, но и числом контактов этой частицы с частицами окружения, через которые передается давление. Например, если мелкая частица попадет в окружение крупных, она окажется в полости между ними и не будет испытывать давления с их стороны. Это число контактов пропорционально отношению площади поверхности частицы к поперечному сечению частицы окружения [6], что и приводит в предлагаемой модели к появлению множителя (d_k/d)². Отношение ρ/d², входящее в (5), определяется локальной концентрацией ключевого компонента c:

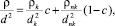(6)

где ρ_nk и d_nk – плотность и диаметр частиц несущего компонента. С учетом (5) и (6) выражение для скорости сегрегации 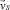(4) с можно записать в виде:

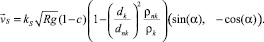(7)

Как отмечалось выше, устройства гравитационно-пересыпного действия могут снабжаться дополнительными рабочими органами – лопатками, которые устанавливаются в радиальном направлении параллельно оси вращения на одинаковом угловом расстоянии друг от друга. Лопатки двигаются синхронно с поверхностью рабочего объема, поэтому не оказывают влияния на процесс при своем прохождении через транспортирующую область, но могут существенно изменять характер движения материала в области активного смешивания, препятствуя развитию потока сегрегации. В предлагаемой модели воздействие лопаток можно учесть, если ввести зависимость коэффициента k_S в (7) от координат и времени:

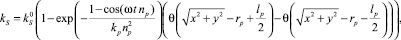(8)

где n_p, r_p, l_p – количество, установочный радиус и длина лопаток соответственно; k_p – модельный коэффициент эффективности воздействия лопатки; 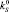 – значение коэффициента k_S при отсутствии лопаток; θ(x) – функция Хэвисайда, равная 0 при x < 0 и равная 1 при x ≥ 0. Согласно выражению (8), при прохождении лопатки через область активного смешивания в зоне воздействия лопатки 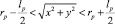величина коэффициента сегрегации k_S и, следовательно, скорость сегрегационного потока 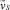существенно снижается.

Уравнение непрерывности (1) с заданными скоростями переноса (2), (3) и (7) с учетом (8) может решаться численно известными методами. Результаты расчетов для средней объемной концентрации ключевого компонента c₀ = 0,3 при коэффициенте загрузки q = 0,4 приведены на рис. 2 и 3. Модельные коэффициенты принимались равными 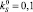, k_p = 1, плотности частиц предполагались равными. На рис. 2 показаны распределения ключевого компонента (темный цвет) по сечению рабочего объема в начальный момент времени (а) и в момент 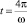для случаев, когда частицы ключевого и несущего компонентов не различаются по физико-механическим свойствам (б) и когда диаметр частиц несущего компонента в два раза превышает диаметр частиц ключевого компонента (в). В случае (б) сегрегация отсутствует и достигается практически равномерное распределение ключевого компонента, в случае (в) ключевой компонент скапливается в окрестности центра вращения, образуя ядро сегрегации, и качество смеси значительно ухудшается.

а б в

Рис. 2. Распределения ключевого компонента в начальный момент времени (а) и в момент t = 4π/ω для случая тождественных частиц (б) и различных частиц (в)

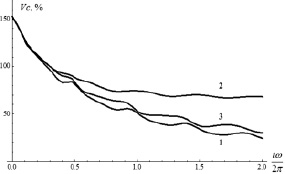
Рис. 3. Изменение коэффициента неоднородности смеси со временем: 1 – без сегрегации; 2 – сегрегация без лопаток; 3 – сегрегация с лопатками

Качество смеси в ходе процесса обычно характеризуется коэффициентом неоднородности Vc [1], который вычисляется по формуле

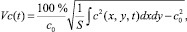(9)

где интегрирование ведется по сечению, занятому смесью, а S = πR²q – площадь этого сечения. На рис. 3 представлены графики зависимости коэффициента неоднородности от времени для случаев, когда частицы ключевого и несущего компонентов не различаются по физико-механическим свойствам (кривая 1) и когда диаметр частиц несущего компонента в два раза превышает диаметр частиц ключевого компонента в отсутствии перемешивающих лопаток (кривая 2) и при наличии четырех лопаток размера l_p = 0,5R, установленных на расстоянии r_p = 0,5R от центра вращения.

Из рис. 3 видно, что установка лопаток существенно улучшает качество смеси, что подтверждается имеющимися экспериментальными данными.

Таким образом, в работе предложена математическая модель процесса смешивания сыпучих материалов в устройстве гравитационно-пересыпного действия, позволяющая вычислять поле концентраций ключевого компонента в плоском сечении рабочего объема в любой момент времени. Модель учитывает сегрегацию смеси, возникающую вследствие различия компонентов по размеру и плотности, а также влияние на процесс дополнительных рабочих органов. Значения свободных параметров модели должны определяться при сравнении результатов расчета с экспериментальными данными. Заметим, что при отсутствии сегрегации, когда смешиваемые фракции не различаются по физико-механическим свойствам, модель не содержит свободных параметров и при этом удовлетворительно согласуется с результатами опытов, что свидетельствует о справедливости лежащих в ее основе предположений.

Рецензенты:

Бачурин В.И., д.ф.-м.н., профессор, Ярославский филиал Московского института инженеров транспорта (университет), г. Ярославль;

Мурашов А.А., д.т.н., профессор, Ярославский филиал Московской финансово-юридической академии, г. Ярославль.

Работа поступила в редакцию 15.07.2014.

Библиографическая ссылка