Образование газовых гидратов в пористых структурах в настоящий момент имеет широкие промышленные перспективы, связанные, в первую очередь, с возможностью хранения газа в гидратном состоянии. В основу гидратного способа хранения газа положено то обстоятельство, что при одинаковых условиях в единице объема в гидратном состоянии содержится значительно больше газа, чем в свободном состоянии [1].
В работах [2–8] были построены в прямолинейно-параллельном приближении математические модели образования газогидрата в пористых средах, изначально насыщенных газом и водой. Однако при выборе подходящих геологических объектов для газогидратной консервации газа более перспективной является пористая среда, частично насыщенная льдом. Важным преимуществом такой среды является то, что интенсивность процесса образования газогидрата в высокопроницаемых пористых средах лимитируется, прежде всего, отводом тепла, а удельная теплота образования газогидрата изо льда в три раза ниже, чем из воды.
В представленной работе в осесимметричном приближении рассмотрены особенности образования гидрата при нагнетании газа в пористый пласт, заполненный в исходном состоянии газом и льдом.
Постановка задачи и основные уравнения. Для описания процессов тепломассопереноса при закачке газа в горизонтальный пористый пласт примем следующие допущения. Процесс однотемпературный, т.е. температуры пористой среды и насыщающего вещества совпадают. Гидрат является двухкомпонентной системой с массовой концентрацией газа G. Кроме того, скелет пористой среды, газогидрат и лед несжимаемы и неподвижны, пористость постоянна, газ – калорически совершенный.
В рамках отмеченных допущений запишем для осесимметричной задачи уравнения сохранения массы, закон Дарси, уравнения состояния газа и притока тепла:
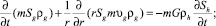
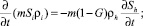
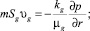
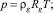(1)
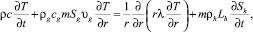
где m - пористость; p - давление; T - температура; ρj и Sj - истинная плотность и насыщенность пор j-й фазы (j = h, i, g); индексы g, i и h относятся к параметрам газа, льда и гидрата соответственно; υn, kg и μg - скорость, проницаемость и динамическая вязкость для газовой фазы; Lh - удельная теплота гидратообразования; cg - удельная теплоемкость Г; ρc и λ - удельная объемная теплоемкость и коэффициент теплопроводности системы.
Зависимость коэффициента проницаемости для газа kg от газонасыщенности можно задать на основе формулы Козени
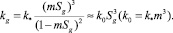
Значения температуры и давления в области образования гидрата связаны условием фазового равновесия:
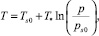(2)
где ps0 – равновесное давление, соответствующее температуре Ts0; T* – эмпирический параметр, зависящий от вида газогидрата.
При образовании газогидрата в пористом пласте возникают зоны, в которых газ, лед и газогидрат могут находиться в различных состояниях. На поверхностях разрыва между этими зонами, где терпят скачки насыщенности фаз, а также потоки массы и тепла, должны выполняться условия баланса массы и тепла:
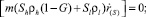
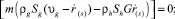(3)
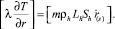
Здесь [ψ] – скачок параметра ψ на границе r(s) между областями;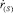 
– скорость движения этой границы. Температуру и давление на границе между областями будем полагать непрерывными.
Будем полагать, что пласт в начальный момент времени насыщен газом и льдом, давление p0 и температура T0 которых в исходном состоянии соответствуют термодинамическим условиям существования их в свободном состоянии (p0 ≤ ps0) и изначально одинаковы во всем пласте. Эти условия могут быть записаны следующим образом:
t = 0: T = T0; p = p0 (r ≥ rw).
Пусть через скважину, вскрывшую пласт на всю толщину, закачивается газ (одноименный исходному) с постоянным массовым расходом Qg (на единицу высоты скважины) при постоянной температуре Tw. С учетом закона Дарси и уравнения состояния для газа условия на границе скважины имеют вид
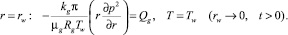
В результате закачки газа вблизи скважины образуется область, насыщенная газом и гидратом. Рассматривая достаточно большие времена после начала нагнетания газа, когда размеры данной области значительно превышают радиус скважины (r(s) >> rw), будем полагать, что размер скважины слабо сказывается на особенностях протекания процесса. Сформулированная задача имеет автомодельное решение.
Рассмотрим решение с фронтальной поверхностью образования гидратов. В данном случае возникают две характерные области. В первой области, находящейся вблизи скважины, лед полностью перешел в газогидратное состояние, поэтому в порах присутствуют только газ и газогидрат. Во второй (дальней) области поры пласта заполнены газом и льдом. Таким образом, в данном случае образование газогидрата полностью происходит на фронтальной поверхности между этими областями, а промежуточная область отсутствует.
Автомодельное решение. Введем автомодельную переменную
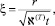
где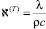 
– коэффициент температуропроводности пласта.
Тогда решение задачи может быть записано в виде
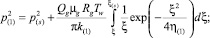
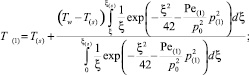(4)
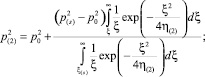
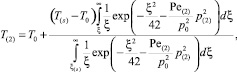(5)
где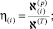 
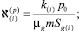
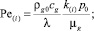
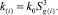Параметры первой и второй областей снабжены нижними индексами в скобках i = 1, 2. Отметим, что решение для распределения давления получено с использованием линеаризации Лейбензона [5].
На поверхности, разделяющей ближнюю и дальнюю области, происходит скачок гидратонасыщенности от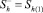 
до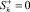 
. Величина гидратонасыщенности первой области Sh(1) определяется из условия баланса массы льда:
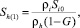
где Si0 – начальная льдонасыщенность.
Для значений температуры и давления на границе между областями выполняется условие фазового равновесия (2).
На основе условий (3) с учетом полученных решений (4) и (5) получим уравнения для определения координаты границы фазовых переходов (ξ = ξ(s)) и значений параметров на ней:
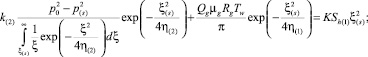
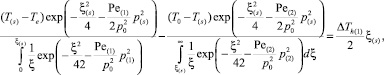(6)
где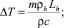 
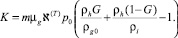
Результаты расчетов.
На основе решений (4) и (5), а также трансцендентных уравнений (6) проведены численные расчеты для случая газогидрата на основе лед - метан. На рис. 1, a представлены распределения температуры и давления при нагнетании газа c массовым расходом Qg = 0,004 кг/(м·с) и с температурой Tw = 265 К в пласт с начальным давлением p0 = 2 МПа и исходной льдонасыщенностью Si0 = 0,2. Для остальных параметров, характеризующих систему, приняты следующие значения: m = 0,1, G = 0,12, T0 = 271 К, T* = 30 К, ps0 = 2,38 МПа, Ts0 = 270 К, k0 = 10-14 м2, ρh = 900 кг/м3, ρi = 900 кг/м3, Rg = 520 Дж/(К∙кг), cg = 1560 Дж/(К·кг), ρc = 2,5·106 Дж/(К·кг), λ = 2 Вт/(м∙К), μg = 10-5 кг/(м∙с), Lh = 1,66·105 Дж/кг. Линия 2 показывает равновесную температуру, соответствующую полученному распределению давления. Из данного рисунка видно, что температура пласта перед фронтом гидратообразования ниже равновесной температуры, а за фронтом - выше этой температуры, что является физически непротиворечивым. Следовательно, в этом случае можно говорить о существовании решения с фронтальной поверхностью образования гидрата.
На рис. 1, б приведены распределения температуры и давления при нагнетании газа c массовым расходом Qg = 0,008 кг/(м·с) и с температурой Tw = 265 К. Видно, что температура пласта за фронтом гидратообразования опускается ниже равновесной температуры (линия 2), т.е. в этой области наблюдается переохлаждение льда. Таким образом, при данном массовом расходе модель с фронтальной поверхностью образования гидрата не позволяет построить физически непротиворечивое решение. Для устранения этого противоречия необходимо вводить протяженную область гидратообразования.
а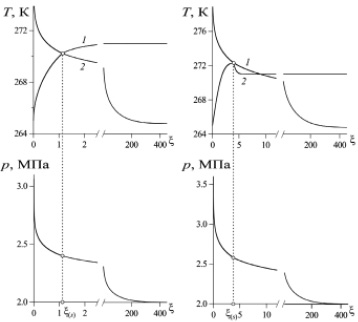
б
Рис. 1. Распределение температуры пласта (1), равновесной температуры (2) и давления. Qg = 0,004 кг/(м∙с) (a) и 0,008 кг/(м∙с) (b)
Объемная область возникает в том случае, когда на границе фазовых переходов (ξ = ξ(s) ) выполняется условие
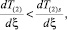
где T(2)s – температура гидратообразования, соответствующая давлению p(2) . Из условия фазового равновесия (2) имеем:
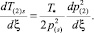
Тогда с учетом полученных решений (4), (5) и системы граничных условий (6) имеем следующее условие существования решения с фронтальной границей образования гидрата:
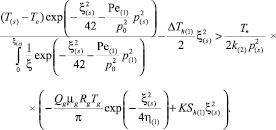(7)
На основе неравенства (7) и системы граничных условий (6) были проведены численные эксперименты в широком диапазоне параметров. Опираясь на результаты численных расчетов, можно сделать вывод о том, что для каждого значения проницаемости существует критическое значение Qcr массового расхода газа, при превышении которого возникает объемная область образования гидрата.
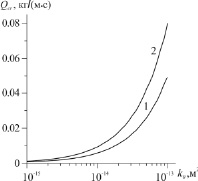
Рис. 2. Критическая диаграмма на плоскости (Qg, k0). p0 = 2 МПа (1) и 1,7 МПа (2)
На рис. 2 показана зависимость критического значения массового расхода от абсолютной проницаемости пласта. Кривые 1 и 2 соответствуют двум разным значениям начального давления пласта: p0 = 2МПа (1) и p0 = 1,7 МПа (2). Из данного рисунка видно, что критическое значение массового расхода Qcr повышается с увеличением проницаемости, причем тем быстрее, чем ниже исходное давление.
Выводы
Таким образом, при инжекции газа в пористую среду, частично насыщенную льдом, образование газогидрата может происходить как на фронтальной поверхности, так и в протяженной области в зависимости от величины массового расхода, проницаемости и исходного пластового давления.
Работа поддержана грантом Российского фонда фундаментальных исследований (проект 14-01-31089).
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор, декан физико-математического факультета Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак;
Биккулова Н.Н., д.ф.-м.н., профессор, заведующая кафедрой общей физики Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак.
Работа поступила в редакцию 10.07.2014.
Библиографическая ссылка
Хасанов М.К., Доровская М.С. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ИНЖЕКЦИИ ХОЛОДНОГО ГАЗА В ПОРИСТУЮ СРЕДУ, ЧАСТИЧНО НАСЫЩЕННУЮ ЛЬДОМ // Фундаментальные исследования. 2014. № 9-4. С. 741-746;URL: https://fundamental-research.ru/ru/article/view?id=34918 (дата обращения: 18.05.2025).