Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Новиков Е.А. 1 Ващенко Г.В. 2

---

1 ФГБУН «Институт вычислительного моделирования СО РАН»

2 ФГБОУ ВПО «Сибирский государственный технологический университет»

Представлен L-устойчивый метод третьего порядка точности для численного решения жестких задач. Этот метод достаточно прост в реализации и обладает хорошими свойствами по точности. Эффективность предлагаемого метода может быть повышена за счет использования алгоритмов с контролем точности вычислений на шаге. Для реализации пошагового контроля нами построен критерий, в основе которого лежит оценка аналога глобальной ошибки. Эта оценка осуществляется с привлечением ранее вычисленных стадий численной схемы, что обеспечивает возможность выбора величины шага интегрирования фактически без увеличения вычислительных затрат. Сформулированы и представлены последовательный алгоритм и параллельная версия MPI-алгоритма с контролем точности вычислений на шаге. Данный метод входит в семейство (m, k)-методов, введенных в работе [5]. В (m,k)-методах стадия метода не связывается с обязательным вычислением правой части исходной задачи. За счет этого их свойства могут быть улучшены. Данные схемы можно рассматривать как способ реализации неявных методов типа Рунге ‒ Кутты. Важно, что при такой реализации не требуются итерации метода Ньютона.

Статья в формате PDF

1748 KB

контроль точности

переменный шаг

(3

2)-метод

параллельный MPI-алгоритм

1. Ващенко Г.В. Построение соотношения изоэффективности параллельного (3,2)-метода для численного решения задачи Коши // Современное состояние естественных и технических наук: мат. X Международной конф. – М.: Изд-во «Спутник+», 2013. – C. 36–41.

2. Демидов Г.В., Юматова Л.А. Исследование некоторых аппроксимаций в связи с А–устойчивостью полуявных методов // Численные методы механики сплошной среды. – 1977. – Т. 8. – № 3. – С. 68–79.

3. Новиков В.А., Новиков Е.А., Юматова Л.А. Замораживание матрицы Якоби в методе типа Розенброка второго порядка точности // ЖВМ и МФ. – 1987. – Т. 27. – № 3. – С. 385–390.

4. Новиков Е.А., Шорников Ю.В. Компьютерное моделирование жестких гибридных систем – Новосибирск: Изд-во НГТУ, 2012. – 450 с.

5. Новиков Е.А., Шитов Ю.А., Шокин Ю.И. Одношаговые безытерационные методы решения жестких систем // ДАН СССР. – 1988. – Т. 301. – № 6. – С. 1310–1314.

6. Демидов Г.В., Юматова Л.А. Исследование некоторых аппроксимаций в связи с А–устойчивостью полуявных методов // Численные методы механики сплошной среды. – 1977. – Т.8. – № 3. – С. 68–79.

7. Новиков Е.А. Явные методы для жестких систем. – Новосибирск: Наука, 1997. – 197 с.

8. Новиков Е.А. Ващенко Г.В. Design of Parallel Algorithm (3,2)-method for Stiff Problems //Second International Conference on Cluster Computing (CC 2013), Lviv, Ukraine, June 3–5, Proceedings, p.165, 2013.

9. Demmel J. Applied numerical linear algebra. SIAM, 1997.

10. Hairer E. and Wanner G. Solving Ordinary Differential Equations II: Stiff and Differential-algebraic Problems. Springer-Verlag, second revised edition, 1996.

11. Rosenbrock H.H. Some general implicit processes for the numerical solution of differential equations // Computer. – 1963. – № 5. – Р. 329–330.

12. Shampine L.M. Implementation of Rosenbrock methods // ACM Transaction on Mathematical Software. – 1982. – Vol. 8, № 5. – Р. 93–113.

Для численного решения жестких систем обыкновенных дифференциальных уравнений обычно применяются L-устойчивые методы [9]. При реализации таких численных схем на каждом шаге несколько раз решается линейная система алгебраических уравнений с применением LU-разложения матрицы Якоби. При большой размерности исходной задачи общие вычислительные затраты фактически полностью определяются временем декомпозиции данной матрицы. Сокращения затрат достигают за счет применения одной матрицы на нескольких шагах [3, 4, 9]. Наиболее естественно это осуществляется в итерационных методах, где данная матрица только определяет скорость сходимости итерационного процесса [9]. Для безытерационных методов типа Розенброка [10] и их модификаций [5, 9] вопрос о замораживании матрицы Якоби более сложный. В таких методах эта матрица включена в численную схему, и поэтому ее аппроксимация приводит к потере порядка точности численной формулы. Максимальный порядок методов типа Розенброка с замораживанием матрицы Якоби равен двум [3]. Безытерационные методы просты с точки зрения реализации и, как следствие, привлекательны для вычислителей. Некоторым аналогом замораживания матрицы Якоби является применение в расчетах алгоритмов интегрирования на основе явных и L-устойчивых методов с автоматическим выбором численной схемы. В этом случае эффективность алгоритма может быть повышена за счет расчета переходного участка, соответствующего максимальному собственному числу матрицы Якоби, явным методом. В качестве критерия выбора эффективной численной формулы естественно применять неравенство для контроля устойчивости [6, 11]. Следует отметить, что применение таких комбинированных алгоритмов полностью не снимает проблему замораживания матрицы Якоби, потому что явным методом можно просчитать, вообще говоря, погранслойное решение, соответствующее максимальному собственному числу матрицы Якоби. В [5] предложен новый класс одношаговых численных схем, которые были названы (m, k)-методами. Они столь же просты при реализации, как и методы типа Розенброка, но обладают более хорошими свойствами точности и устойчивости. Более существенно, они достаточно просто реализуются с замораживанием матрицы Якоби.

Здесь разработан L-устойчивый (3,2)-метод третьего порядка точности для решения жестких задач. Построено неравенство для контроля точности вычислений, основанное на оценке аналога глобальной ошибки. Оценка осуществляется с привлечением ранее вычисленных стадий, что позволяет выбирать величину шага интегрирования фактически без увеличения вычислительных затрат. Сформулирован последовательный алгоритм и его параллельный аналог – MPI-алгоритм.

1. Класс (m, k)-методов решения жестких задач

Рассмотрим задачу Коши для системы дифференциальных уравнений вида

y′ = f(y); y(t₀) = y₀; t₀ ≤ t ≤ tk, (1)

где y и f – вещественные N-мерные вектор-функции; t – независимая переменная. Пусть Z – множество целых чисел, и заданы числа m, k ∈ Z, k ≤ m. Обозначим через M_m множество чисел {i ∈ Z, 1 ≤ i ≤ m}, а через M_k и J_i, 1 < i ≤ m подмножества из M_m вида

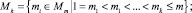
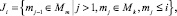
где 1 ≤ i ≤ m. Тогда класс (m, k)-методов записывается следующим образом [5]:

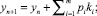
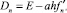
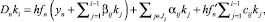i ∈ Mk, (2)

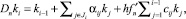i ∈ M_m\M_k,

где k_i, 1 ≤ i ≤ m, - стадии метода; a, p_i, β_ij, α_ij и c_ij - постоянные коэффициенты; h - шаг интегрирования; E - единичная матрица; f′_n = ∂f(y_n)/∂y - матрица Якоби системы (1); k - количество вычислений функции f на шаге; m - число стадий. На каждом шаге интегрирования осуществляются одно вычисление матрицы Якоби и одна декомпозиция матрицы D_n. Так как k и m полностью определяют затраты на шаг, а набор чисел m₁, ..., m_k из множества M_k только распределяет их внутри шага, то методы типа (2) названы (m, k)-методами. Основное отличие приведенных методов (2) от существующих численных формул состоит в том, что в них стадия метода не связывается с обязательным вычислением правой части исходной задачи (1), за счет этого свойства методов могут быть улучшены.

При k = m и α_ij = c_ij = 0 схемы (2) совпадают с методами типа Розенброка [10], а при k = m и α_ij = 0 – с ROW-методами [9]. В отличие от ROW-методов в численных формулах (2) более точно определены затраты на шаг интегрирования и более правильно описана область определения коэффициентов численных формул, что упрощает их исследование и делает их предпочтительнее. При рассмотрении методов такого типа в основном изучался случай k = m, то есть когда число стадий и количество вычислений правой части задачи (1) совпадают. В этом случае k-стадийную схему (2) можно поставить в соответствие k-стадийной полуявной формуле типа Рунге ‒ Кутты, при реализации которой на каждом шаге используется одна матрица размерности N. Относительно таких численных формул известно, что нельзя построить k-стадийную схему выше (k + 1)-го порядка точности, причем схема максимального порядка A-устойчивая. Если рассматривать схемы (2) при m > k, то можно построить численные схемы более высокого порядка точности [5].

2. Исследование (3, 2)-метода

Рассмотрим численную формулу вида

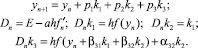(3)

Разлагая стадии k_i, 1 ≤ i ≤ 3 в ряды Тейлора и подставляя в первую формулу (3), получим ряд Тейлора для приближенного решения y_n + 1. Полагая y_n = y(t_n) и сравнивая ряды для точного и приближенного решений, получим условия третьего порядка точности схемы (3), то есть

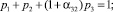
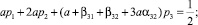
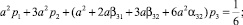
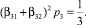
Положим a, β₃₁ и β₃₂ свободными и исследуем эту систему на совместность. Получим

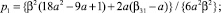
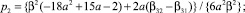(4)

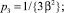
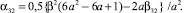
где β = β₃₁ + β₃₂. Исследуем устойчивость схемы (3) на линейном скалярном уравнении y′ = λy, где смысл комплексного числа λ, Re(λ) < 0, – некоторое собственное число матрицы Якоби задачи (1). Применяя (3) для решения этого уравнения, получим y_{n + 1} = Q(z)y_n, где z = hλ, а функция устойчивости Q(z) записывается следующим образом:

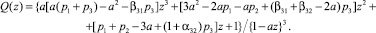
Из вида Q(z) следует, что для L-устойчивости схемы (3) необходимо выполнение соотношения

Подставляя сюда коэффициенты (4), получим уравнение

Далее, сравнивая представление приближенного и точного решений до членов с h⁴ включительно, видим, что слагаемые с элементарными дифференциалами f′′′f³ и f′′f′f² в главном члене локальной ошибки будут отсутствовать, если

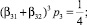
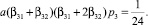
Теперь отсюда и (4) получим набор коэффициентов

,

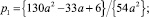
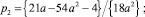
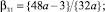
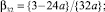
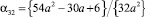при которых локальная ошибка δ_n,3 схемы (3) имеет вид

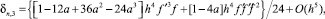
где значение a определяется из условия L-устойчивости

a³ – 3a² + 1,5a – 1/6 = 0.

Это уравнение имеет три вещественных корня. Согласно [2] требование A-устойчивости схемы (3) имеет вид 1/3 ≤ a ≤ 1,0685790, поэтому выбираем корень a = 0,435866521508459.

В жестких задачах поведение ошибки определяется элементарным дифференциалом f′³f [5]. Поэтому при построении оценки аналога глобальной ошибки будем учитывать только первое слагаемое в локальной ошибке. Для контроля точности вычислений и автоматического выбора величины шага интегрирования используем идею вложенных методов. Для этого рассмотрим двухстадийный метод (2) вида

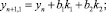
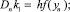
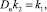(5)

где y_n вычислено по формуле (3). В численной формуле (5) применяются стадии метода (3), и поэтому она практически не приводит к увеличению вычислительных затрат. Нетрудно видеть, что при коэффициентах b₁ = 0,5(4a – 1)/a и b₂ = 0,5(1 – 2a)/a схема (5) имеет второй порядок точности, а ее локальная ошибка имеет вид

δ _n,2 = (6a² – 6a + 1)h³ f′²f/6 + O(h⁴).

Тогда в неравенстве для контроля точности можно применять оценку ошибки ε_n(j_n) вида [5]

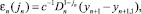(6)

где

c = 4·|6a² – 6a + 1|/|1 – 12a + 36a² – 24a³| ≈ 3.

При j_n = 1 оценка ε_n(j_n) будет A-устойчивой, а при j_n = 2 – L-устойчивой. Теперь неравенство для контроля точности имеет вид

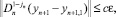1 ≤ jn ≤ 2, (7)

где ε – требуемая точность интегрирования, а параметр j_n выбирается с наименьшим значением, при котором выполняется неравенство (7). Норма ||ξ|| в (7) вычисляется по формуле

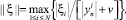
В случае выполнения неравенства 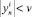по i-й компоненте решения контролируется абсолютная ошибка vε, в противном случае контролируется относительная ошибка ε.

3. Последовательный алгоритм интегрирования и его параллельная версия

Запишем схему (3) в покомпонентной форме, имеем

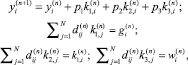(8)

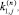
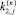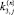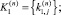
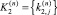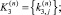
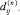
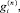
где 1 ≤ i ≤ N, и есть элементы векторов приращений 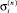и и 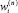есть элементы матрицы D_n и векторов g⁽ⁿ⁾ , σ⁽ⁿ⁾ , w⁽ⁿ⁾ ;

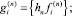
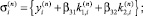
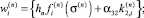
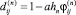
при i = j и 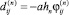при i ≠ j. Здесь 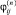– элементы матрицы Якоби 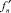задачи (1), вычисленные на решении y(n), 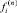– элементы вектора правой части f(y). Применение LU-разложения [8] приводит к системам уравнений для нахождения стади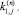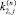й и 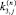, то есть

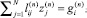
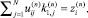1 ≤ i ≤ N;

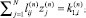
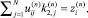1 ≤ i ≤ N; (9)

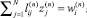
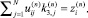1 ≤ i ≤ N,

где 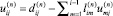при i ≤ j и 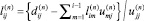при i > j.

Используя обозначения элементов обратной матрицы 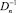через 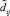, нормы ошибок вычисляем по формулам

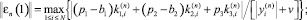(10)

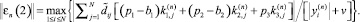(11)

Пусть приближение y_n к решению y(t_n) задачи (1) вычислено в точке t_n с шагом h_n. Тогда учитывая, что имеет место 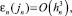1 ≤ j_n ≤ 2, последовательный алгоритм интегрирования формулируется следующим образом.

Шаг 1, 2. Вычислить матрицу Якоби 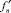и сформировать матрицу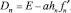

Шаг 3. Выполнить декомпозицию матрицы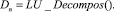

Шаг 4, 5. Вычислить

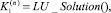
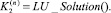
Шаг 6, 7. Вычислить

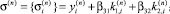
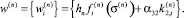
Шаг 8. Вычислить

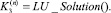
Шаг 9, 10. Вычислить норму ошибки 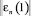по формуле (10) и q₁ по формуле

.

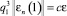Шаг 11. Если q₁ < 1, то есть требуемая точность не достигнута, то вычисляется 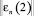по формуле (11). В противном случае 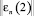полагается равным .

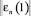Шаг 12. Вычислить значение параметра q₂ по формуле .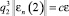

Шаг 13. Если q₂ < 1, то hn полагается равным q₂h_n и возврат на шаг 2.

Шаг 14. Вычислить приближение к решению в точке tn + 1 по формуле (8), то есть

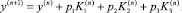
Шаг 15. Вычислить значение h_{n + 1} по формуле h_{n + 1} = min(q₁, q₂)h_n.

Шаг 16. Выполнить следующий шаг интегрирования.

Замечание

При численном вычислении матрицы Якоби шаг численного дифференцирования r_i, 1 ≤ i ≤ N, выбирается по формуле [6]

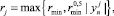1 ≤ j ≤ N,

где r_min – минимальный шаг численного дифференцирования, зависит от разрядности вычислительной системы. При расчетах с двойной точностью величину r_min следует принять равной 10^–14. Тогда j-й столбец 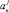численной матрицы вычисляется по формуле

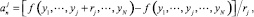
то есть для задания матрицы требуется N вычислений правой части системы дифференциальных уравнений (1).

Если рассматривать алгоритм (3, 2)-метода (3), (8) как объект для распараллеливания, то его последовательный вариант выглядит как процесс вычисления векторов приращений 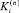, 1 ≤ i ≤ 3. При этом на каждом n-м шаге вычисления имеют последовательный порядок, 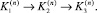При построении параллельного алгоритма необходимо сохранить этот порядок вычисления. Элементы каждого из векторов приращений получаются из решения систем линейных уравнений с одинаковой матрицей D_n и разными правыми частями.

Предположим, что размерность N системы (1) связана с размером p вычислительной системы соотношением N = s·p. Для Dn выберем блочно-строчную схему хранения. Тогда параллельный аналог (3,2)-метода (3) запишется в виде [7]

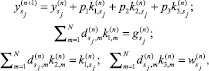(12)

где 1 ≤ i ≤ p, .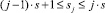

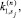
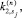
Теперь сформулируем параллельный алгоритм вычисления приближенного решения с контролем точности вычислений. Для контроля точности в (12) используем процессор pr(1). Пусть известно приближение y⁽ⁿ⁾ в точке t_n с шагом h_n. Тогда для вычисления y^{(n + 1)} в точке t _{n + 1} справедлив параллельный алгоритм, в котором на каждом процессоре pr(j) формируется своя s_j-я часть матрицы D_n, векторов 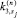и вектора решения .

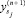Шаг 1. В каждом pr(j), 1 ≤ i ≤ p, :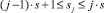

а) выполнить recv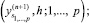

б) вычислить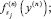

в) вычислить матрицу Якоби.

Шаг 2, 3. Сформировать матрицу 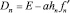и разложить

.

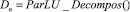Шаг 4, 5. Вычислить

.

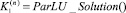
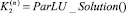Шаг 6. В каждом pr(j), 1 ≤ i ≤ p, :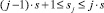

а) выполнить

recv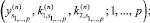

б) вычислить

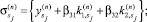
в) выполнить send .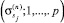

Шаг 7. В каждом pr(j), 1 ≤ j ≤ p, :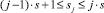

а) выполнить recv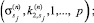

б) сформировать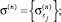

в) вычислить 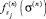и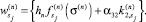

Шаг 8. Вычислить

.

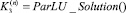Шаг 9. В каждом pr(j), 1 ≤ j ≤ p, :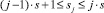

а) вычислить

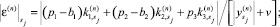
б) вычислить

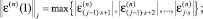
в) вычислить

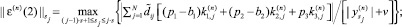
г) вычислить

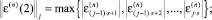
д) send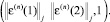

Шаг 10. В pr(1):

а) выполнить

recv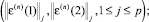

выполняется последовательность действий по контролю точности и вычисление значения h_n;

б) выполнить send (h_n, rp; 1, …, p). При rp = 1 – возврат на шаг 2, при rp = 0 – переход на шаг 11.

Шаг 11. В каждом pr(j), 1 ≤ j ≤ p, :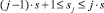

а) выполнить recv (h_n, rp; 1);

б) вычислить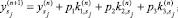

в) выполнить send .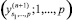

Шаг 12. В pr(1):

а) вычислить h _{n + 1} по формуле

h _{n + 1} = min(q₁, q₂)h_n;

б) send (h _{n + 1}; 1, …, p).

Шаг 13. Выполнить следующий шаг интегрирования.

Замечание

Представленный алгоритм является параллельно-последовательным. В нем не учтены фрагменты, относящиеся к вычислению правой части (1) и матрицы Якоби, а также обращение матрицы Якоби, необходимое при невыполнении неравенства по точности. Для LU-разложения используется частичный выбор по столбцу.

В (m, k)-методах стадия метода не связывается с обязательным вычислением правой части исходной задачи. За счет этого их свойства могут быть улучшены. Данные схемы можно рассматривать как способ реализации неявных методов типа Рунге – Кутты. Важно, что при такой реализации не требуются итерации метода Ньютона, а все проблемы решаются за счет выбора шага интегрирования. Построена параллельная MPI-версия алгоритма интегрирования переменного шага, ориентированная на кластерные системы и топологию полного графа. В [1] построено соотношение изоэффективности, которое может быть использовано для сравнения различных параллельных алгоритмов решения одной и той же задачи Коши на основе (3,2)-метода, а также подходов к выбору и построению алгоритмов вычисления матрицы Якоби и алгоритмов ее факторизации. В особенности это относится к оценке коммуникационных затрат при организации межпроцессорных обменов.

Работа выполнена при финансовой поддержке РФФИ (проект 14-01-00047).

Рецензенты:

Белолипецкий В.М., д.ф.-м.н., профессор, главный научный сотрудник, ФГБУН «Институт вычислительного моделирования» СО РАН, г. Красноярск;

Плотников С.М., д.т.н., профессор, ФГБОУ ВПО «Сибирский государственный технологический университет», г. Красноярск.

Работа поступила в редакцию 10.07.2014.

Библиографическая ссылка