Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Казаров Б.А. 1 Алтухов В.И. 2 Дядюк М.Н. 2 Митюгова О.А. 3

---

1 Кавминводский институт (филиал) ФГБОУ ВПО «Южно-Российский государственный политехнический университет (НПИ) им. М.И. Платова»

2 Филиал ФГАОУ ВПО «Северо-Кавказский федеральный университет»

3 Северо-Кавказский филиал ФГБОУ ВПО «Белгородский государственный технологический университет им. В.Г. Шухова»

В работе рассмотрены механизмы рассеяния фононов и представлена теория температурного поведения теплопроводности кристаллов с фазовыми переходами и дефектами. В модели Дебая проведены расчеты температурной зависимости теплопроводности сегнетоэлектрических кристаллов триглицинсульфата. В работе показано, что нетипичное поведение кривой теплопроводности вблизи температуры структурного фазового перехода Тс связано с крайне узким интервалом температур, в котором проявляются критические флуктуации в одноосных кристаллах. Показано, что аномальное поведение кривой теплопроводности К(Т) около температуры структурного фазового перехода Тс в кристаллах триглицинсульфата связано с осреднением фононных времен релаксации в области относительно высоких значений температур, при которых происходит сегнетоэлектрический фазовый переход, в условиях которого критическое упругое и неупругое рассеяние фононов проявляется в виде резко выраженного узкого минимума. Результаты расчетов согласуются с данными соответствующих экспериментов.

Статья в формате PDF

832 KB

сегнетоэлектрики

структурный фазовый переход

теплопроводность

модель Дебая

критическое рассеяние

фонон

1. Белов А.А. Исследование теплопроводности сегнетоэлектрических кристаллов с фазовым переходом типа порядок-беспорядок и смещения: автореф. дис. ... канд. физ.-мат. наук. – М., 1992. – 20 c.

2. Алтухов В.И., Струков Б.А., Катрышева М.В. Критическое рассеяние фононов и особенности теплопроводности ферроэлектриков // Микросистемная техника. – 2003. – № 4. – С. 69–74.

3. Струков Б.А., Леванюк А.П. Физические основы сегнетоэлектрических явлений в кристаллах. – М.: Наука, 1995. – 304 с.

4. Струков Б.А., Якушин Е.Д. Влияние крупномасштабных неоднородностей на фазовый переход в сегнетоэлектрических монокристаллах триглицинсульфата // Письма в ЖЭТФ. – 1978. – т. 28, вып. 1. – С. 16.

5. Балагуров Б.Я. Затухание высокочастотного звука и теплопроводность в сегнетоэлектриках типа смещения // ЖЭТФ. – 1971. – Т. 61, в. 4. – C. 1627–1635.

6. Алтухов В.И., Ростова А.Т., Казаров Б.А. Рассеяние фононов на точеч­ных дефектах структуры, комплексах-наночастицах и типичные осо­бенности теплового сопротивления реальных кристаллов и сегнетоэлектриков // Нано- и микросистемная техника. – 2006. – № 3. – С. 11–19.

7. Алтухов В.И. Основы теории кинетических свойств кристаллов с дефектами и фазовыми переходами: диэлектрики и сегнетоэлектрики. – Ставрополь: СевКавГТУ, 2003. – 190 с.

8. Алтухов В.И. Симметрия и структурные фазовые переходы в кристал­лах. – СевКавГТУ: Ставрополь, 2003. – 96 с.

9. Марадудин А. Дефекты и колебательный спектр кристаллов: пер. с англ. – М.: Мир, 1968. – 432 с.

10. Altukhov V.I., Strukov B.A. The critical phonon scattering and peculiarities of the thermal conductivity in ferroelectrics // Cond. Matt. Phys. – 2002. – Vol.5., № 4. – P. 769–776.

11. Strukov B.A., Belov A.A. Heat transport properties of ferroelectrics and related materials // Phase transition. – 1994. – Vol.51. – P. 175.

12. Callaway J. Model for Lattice Thermal conductivity at Low Temperatures // Phys. Rev. – 1959. – Vol. 113, № 4. – Р. 1046–1051.

13. Levanyuk A.P., Sigov A.S. Defects and Structural Phage Transition. – New-York, Gordon and Breach, 1988.

14. Strukov B.A., Belov A.A. and Altukhov V.I. Study of phonon scattering processes in displacive ferroelectrics by means of heat conductivity measurement // Ferroelectrics. – 1994. – Vol.9. – Р. 25–30.

Одноосные бездефектные («идеальные») монокристаллы триглицинсульфата (ТГС) являются известными модельными объектами феноменологической теории фазовых переходов второго рода. Дело в том, что имеющее место в одноосных сегнетоэлектриках относительное подавление флуктуаций поляризации дальнодействующими (кулоновскими) силами [3, 4] приводит к расширению (по сравнению с многослойными сегнетоэлектриками и фазовыми переходами неэлектрической природы) области применимости теории Ландау – Гинзбурга. Соответственно сужается область температур (ΔT_L ≤ 0,2–0,3 °K) около Т_с, в которой наблюдаются критические аномалии в поведении термодинамических характеристик этих кристаллов. В частности, в одноосных кристаллах ТГС в непосредственной близости около Т_с разными авторами наблюдались аномалии лямбда-типа для теплоемкости, упругих модулей, коэффициента теплового расширения, коэффициента теплопроводности К(Т) [2, 6–8, 10, 11, 14], которые обычно связывают с наличием флуктуационных эффектов в области температур вблизи точки фазового перехода Тс. Температурная зависимость коэффициента теплопроводности К(Т) кристаллов ТГС (NH₂CH₂COOH)₃H₂SO₄ (температура Дебая θ = 190 °K) измерялась для трех основных кристаллографических направлений [001], [010], [100]. Вдали от точки фазового перехода (Т_с = 322 °K) кривые К(Т) имеют обычный для диэлектрических кристаллов вид: «фононный горб» в области низких температур (T < 25 °K << θ), экспоненциальный спад с ростом Т в интервале 25 < T < 70 °K, убывание по закону K(T) ~ T^–1 в области 100–260 °K и отклонение (спад медленнее, чем 1/Т) при T > 260 °K; при T ≥ 315 °K начинается незначительное возрастание значений К(Т) с ростом температуры. В окрестности точки Тс наблюдается очень узкий (ΔTK ≈ │T – Tc│ ≤ 1 °K), глубокий минимум («провал») на кривой теплопроводности К(Т). Такое поведение кривой К(Т) около Тс характерно только для одноосных кристаллов ТГС и отличается от пяти возможных, ранее описанных в [2, 6, 9, 12, 20], типичных критических аномалий температурной зависимости теплопроводности в кристаллах со структурными фазовыми переходами и дефектами. Поведение теплопроводности в окрестности сегнетоэлектрического фазового перехода второго рода было рассмотрено в работе [5]. Теория влияния рассеяния на дефектах на решеточную теплопроводность содержится в работах [7, 8]. Влияние дефектов на поведение критических аномалий и тепловое сопротивление кристаллов (W = K^–1) вблизи Тс рассматривалось в работах [7, 13].

В настоящей работе представлена теория температурного поведения теплопроводности кристаллов с фазовым переходом и дефектами. В модели Дебая проведены расчеты зависимости К(Т) для ТГС и показано, что нетипичное поведение кривой К(Т) около Тс в кристаллах ТГС связано с крайне узким интервалом температур ΔT_L << ΔT_K (ΔT_K ≤ 1 °K), в котором проявляются критические флуктуации в одноосных кристаллах. Кроме того, существенным оказывается осреднение фононных времен релаксации в области относительно высоких значений температур (T ≈ T_c > θ), при которых происходит сегнетоэлектрический фазовый переход в кристаллах ТГС. Показано, что в этих условиях неупругое рассеяние тепловых фононов на критических колебаниях или квазиупругое рассеяние (на центральном пике) будут проявляться на кривой К(Т) в виде крайне узкого симметричного минимума («провала»), обнаруженного в [3] на кристаллах ТГС около Тс. Результаты расчетов сопоставляются с данными экспериментов.

1. Модель температурного поведения теплопроводности в кристаллах с фазовыми переходами и дефектами. Для коэффициента теплопроводности (К) гармонического кубического кристалла с примесями или дефектами (кластерами, коллоидами, доменами) ранее была получена формула типа Кубо ‒ Гринвуда [7, 8]:

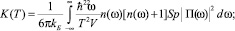(1)

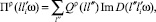(1а)

где V – объем кристалла; Q – величина, связанная с массами и силовыми постоянными атомов в узле l кристаллической решетки; D(ω) – функция Грина реального кристалла с гамильтонианом Н.

1.1. Расчетная формула в простой модели Дебая. Бездефектный («идеальный») кристалл. Для расчета температурной зависимости K(T) в простой дебаевской модели кристалла с фазовым переходом с учетом (1) получаем

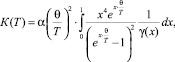(2)

где α – коэффициент при интеграле теплопроводности, связанный с квадратом скорости фононов; θ – характеристическая температура кристалла (температура Дебая); γ(x) – сумма обратных времен релаксации, обусловленных рассеянием фононов в исходном («идеальном») кристалле (γ0), за счет механизмов структурного фазового перехода (γ_C = γ_n + γ_e), дефектов и их комплексов (γk) и за счет резонансного рассеяния на примесях (γ_r).

Скорость релаксации фононов в «нормальном» (не испытывающем фазового перехода) кристалле обычно можно представить следующим выражением [7, 8]:

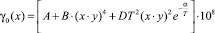с^–1, (3)

где x = ω/ω_D, ω_D = k_Бθ/ћ и А, В, D, α – параметры времен релаксации, выбираются на основе наилучшего согласия результатов расчета с данными экспериментов для чистого («идеального») кристалла.

1.2. Критическое рассеяние фононов. При наличии в системе фазового перехода (кристаллы ТГС [3]) для неупругого рассеяния тепловых фононов ω на критических ω₀ = ω₀(T) имеем формулу [7, 13]:

(4)

где ω₀ и 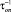– частота и затухание мягкого (критического) фонона; В – коэффициент пропорциональности и β^–1 = k_БT.

Квазиупругое рассеяние фононов с учетом, что частота мягкой моды 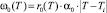[7, 8], можно представить обратным временем релаксации 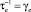в виде [8]:

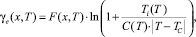(5)

где

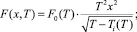
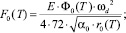
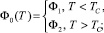
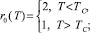
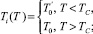
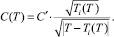
Численные значения постоянных α0, C′, E, Φ₁ и Φ₂ определяются характером поведения ω₀(T) и К(Т) около Тс [3].

1.3. Резонансное рассеяние фононов. Точечные дефекты, туннелирование или кластеры. Для описания обратного времени релаксации, обусловленного рассеянием фононов на кластерах (коллоидах или наночастицах) со средним радиусом r и концентрацией N в работе было использовано выражение [7]:

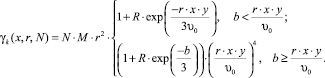(6)

Здесь R - параметр, зависящий от упругих свойств коллоида и матрицы; b - постоянная, связанная с R; M = π∙υ₀∙10³; υ₀, y, x - приведенные скорость, температура Дебая и частота фонона соответственно; x = ω/ω_D, ω_D = k_Бθ/ћ - дебаевская частота кристалла; k_Б - постоянная Больцмана.

Для обратного времени релаксации 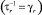, определяющего резонансное рассеяние фононов на точечных дефектах или туннельных (двухуровневых) системах, будем использовать следующее модельное выражение 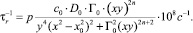[7]:

(7)

Здесь с₀ - концентрация примесей или дефектов (систем), ω_D ≡ yp∙(p = 1013 с^-1, Γ₀ = 6, D₀ = 1,21∙10⁶), n = 4 или 1, 2, 3 и зависит от характера рассеяния фононов на резонансной частоте x = ω/ω_D, связанной с примесью, дефектом, с туннельными (спиновыми) уровнями или другими фононными резонансами (например, двухуровневые системы в спиновых стеклах).

2. Результаты расчетов и сопоставление с данными опытов. Формулы (2)–(7) со скоростью релаксации γ = γ₀ + γ_c + γ_k + γ_r были использованы для расчета кривых теплопроводности К(Т) кристаллов ТГС. Результаты расчетов сопоставляются с данными соответствующих экспериментов (рис. 1, 2 и 3).

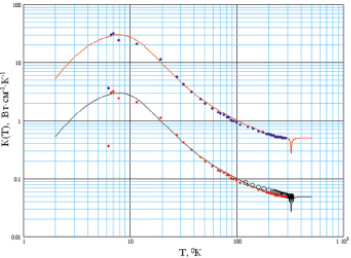
Рис. 1. Температурная зависимость теплопроводности «номинально чистых» кристаллов ТГС в широком интервале температур 6–340 °K [20]. Сплошные линии – расчет; нижняя кривая К(Т) смещена вниз на порядок и при T > 100 °K, кружочками приведены данные из [20]

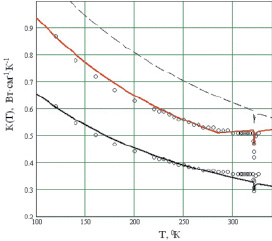
Рис. 2. Температурная зависимость теплопроводности кристаллов ТГС в области температур 100–335 °K [20]. Сплошные линии – расчет; верхняя и нижняя кривые смещены относительно исходных данных [20] для наглядности и приведены без учета отклонения от закона Эйкина 1/Т

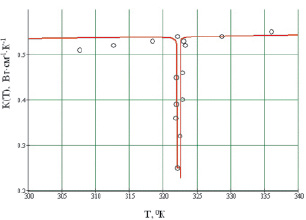
Рис. 3. Температурное поведение теплопроводности высококачественных кристаллов ТГС около Tc = 322 °K в направлении [001] [11]. Сплошная линия – расчет: в теории незначительное возрастание К(Т) при T > 300 °K специально оставлено таким, как на рис. 2 (кривая 2 сверху)

В области T < 7 °K резкий спад К(Т) при T → 0, возможно, связан с рассеянием фононов на кластерах, коллоидах или доменах. Конечно, рассеяние фононов на границах образцов кристалла требует в данном случае специального рассмотрения как на опыте (одна точка, рис. 1), так и в теории. Резонансное рассеяние на примесях или туннелирование играет заметную роль в формировании прогиба кривой К(Т) в области 20 < T < 200 °K (рис. 2). Рассеяние тепловых фононов на критических или центральном пике (ЦП) определяет поведение теплопроводности К(Т) непосредственно вблизи Тс в узком интервале температур порядка нескольких градусов (рис. 2, 3).

3. Обсуждение и выводы. Как было сказано выше, на рис. 1 слева от максимума (T < T_m ≅ 7 °K) на кривой К(Т) наблюдается резкое (на порядок) уменьшение теплопроводности при T ≅ 6 °K. В ходе расчетов нам не удалось получить такого резкого изменения (почти излом) поведения кривой К(Т) при T < T_m ни путем изменения параметра А в γ₀ (рассеяние фононов на границах образца), ни путем включения эффективного при T → 0 рассеяния фононов γ_k на возможных замороженных в образце кластерах (доменах или комплексах из наночастиц). Однако здесь (ТГС, рис. 1) при T < T_m на опыте имеется лишь одна точка, и поэтому эта ситуация требует более детального изучения, тем более что имеются данные еще для ряда систем [10] с подобным поведением кривой К(Т) при T → 0.

Следует отметить, что при моделировании поведения кривой теплопроводности приходится использовать до 10 свободных параметров, однако сразу 5–8 из них (А, В, D, a, C, Θ), как правило, определяются из кривых для «идеальных» чистых образцов и имеют хорошо выверенный физический смысл и известные границы своих значений [2, 6]. Кроме того, иногда удается определить их значения из независимых опытных данных. Остальные 2–3 параметра последовательно подбираются из соображений наилучшего (до 1–2 %) согласия с данными опытов, как правило, полученных для 3–4 до 6–7 образцов кристаллов.

В области достаточно высоких температур при T > θ = 190 °K наблюдается выход кривой К(Т) на плато (К(Т) = const), отклонение спада К(Т) от закона Эйкина 1/Т (регулярное поведение) и даже незначительное возрастание зависимости К(Т) при Т свыше 315 °К [8] (рис. 2 и 3). Такое поведение К(Т) при T > θ скорее всего связано с достаточно сильной при таких температурах перенормировкой третьего слагаемого в γ0, ответственного за ангармоническое взаимодействие фононов (D → DT/θ ≅ DT/200) и актуального при T > θ = 190 °K. Возможно, это связано и с искажением за счет сил ангармонизма при T > θ туннельных состояний (водородных связей) в решетке ТГС. Надо отметить, что при описании переноса тепла в кристаллах при T > θ необходимо учитывать роль оптических фононов, а также возможную (при T > θ) зависимость частоты Дебая ω_D от температуры.

Таким образом, в ситуации, когда критические флуктуации (как в одноосном кристалле ТГС) относительно подавлены, а роль отдельных механизмов релаксации фононов при достаточно сильном ангармонизме (T > θ) нивелирована («осреднена»), влияние критического рассеяния фононов около Т_с резко выражено. В этом случае в узкой области ΔT_k, возможно, реализуется особое неравновесное (метастабильное или типа «спиновое стекло») состояние системы. При этом аномальное поведение теплопроводности вблизи Т_с может оказаться весьма ярким – в крайне узком интервале температур ΔT_K появляется глубокий минимум (провал: рис. 3).

Рецензенты:

Янукян Э.Г., д.ф.-м.н., профессор, декан инженерного факультета, профессор кафедры физико-математических дисциплин, филиал СКФУ, г. Пятигорск;

Чернобабов А.И., д.ф.-м.н., профессор кафедры физико-математических дисциплин, филиал СКФУ, г. Пятигорск.

Работа поступила в редакцию 10.07.2014.

Библиографическая ссылка