Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

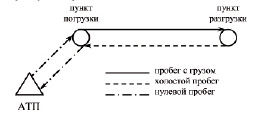
Рис. 1. Схема работы маятникового маршрута с обратным незагруженным пробегом

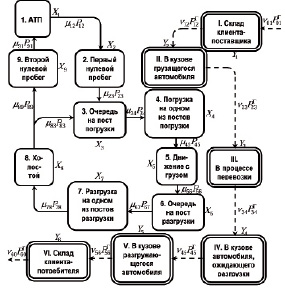
Рис. 2. Совмещенный граф перемещения автомобилей и единиц груза

Блоками с одинарным контуром на рис. 2 обозначены возможные состояния автомобилей, а сплошными стрелками направления перехода из одного состояния в другое. Через Х_i (i = 1,2,...,9) на рис. 2 обозначено мгновенное количество автомобилей в соответствующем i-ом состоянии, через m – интенсивность перехода одного автомобиля из данного i-гo в последующее j-ое состояние, а через Р_ij– вероятность такого перехода. Под интенсивностью перехода одного автомобиля из данного состояния в последующее будем понимать величину, обратную времени пребывания автомобиля в i-ом состоянии, т.е.

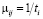, (1)

где t_i – время пребывания автомобиля в i-ом состоянии.

Каждому состоянию графа переходов системы будет соответствовать дифференциальное уравнение вида

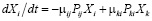. (2)

Это уравнение определяет скорость изменения количества автомобилей в рассматриваемом состоянии (dX_i/dt) как разность между суммарной интенсивностью перехода автомобилей в данное i-ое состояние из предыдущего k-го и суммарной интенсивностью перехода из данного i-гo в последующее j-ое состояние [2]. Тогда рассматриваемому графу переходов будет соответствовать система из девяти дифференциальных уравнений:

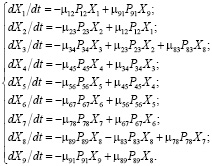
Для интегрирования этой системы необходимо задать значения вероятностей Р_ij и интенсивностей μ_ij переходов из одного состояния в другое, а также начальные условия интегрирования.

Вероятности переходов автомобилей из одного состояния в другое используем для управления движением автомобилей. Для этого будем рассматривать их как булевы переменные, принимающие значение 0, если данный переход из одного состояния в другое необходимо запретить, и 1, если такой переход разрешен.

Будем считать, что вероятности переходов P₂₃, P₃₄, P₄₅, P₅₆, P₆₇, P₇₈ и P₉₁ всегда равны единице. Вероятности P₁₂, P₈₃ и P₈₉ могут принимать значения 0 или 1 и связаны между собой следующей зависимостью: если P₁₂ = 0, то P₈₉ может принимать значения 0 или 1, если P₈₃ = 1, то P₈₉ может иметь только нулевое значение, и наоборот. Для вероятностей P₈₃ и P₈₉ установим следующую зависимость: P₈₃ = 0, если P₈₉ = 1, и P₈₃ = 1, если P₈₉ = 0.

Перейдем теперь к определению интенсивностей переходов из одного состояния в другое μ_ij. Отметив, что интенсивность перехода автомобиля из какого-либо состояния есть величина обратная времени пребывания автомобиля в этом состоянии, выразим ее через значения параметров транспортного процесса [2]. Проще всего это сделать для состояний, отражающих процесс перемещения автомобиля по маршруту (состояния 2, 5, 8, 9). При этом соответствующие интенсивности примут следующие значения:

(4)

где l₀ – длина нулевого пробега (расстояние от склада поставщика до автотранспортного предприятия);

l_М – длина маршрута (расстояние от склада поставщика до склада потребителя);

v_ТГ – скорость движения автомобиля с грузом;

v_ТХ– скорость движения автомобиля без груза.

Несколько сложнее определить интенсивности μ₄₅ и μ₇₈ переходов из состояний погрузки и выгрузки. В общем случае с увеличением числа автомобилей в этих состояниях в пределах от X_i = 0 до X_i = mi (где m_i – число постов погрузки или выгрузки в рассматриваемом состоянии) суммарная интенсивность перехода μ_ij X_i растет от нуля до значения

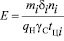, (5)

где δ_i – грузоподъемность погрузочной (или разгрузочной) машины в рассматриваемом состоянии;

n_i – количество погрузочных (или разгрузочных) машин на одном посту;

q_Н – грузоподъемность автомобиля;

γ_C – коэффициент использования грузоподъемности автомобиля;

t_Цi – время цикла погрузочной (или разгрузочной) машины.

При дальнейшем увеличении числа автомобилей в соответствующем состоянии появляется очередь (простой в ожидании погрузки или выгрузки) и величина X_i μ_ij остается неизменной, как показано на рис. 3.

Рис. 3. График зависимости суммарной интенсивности переходов автомобилей из состояния погрузки или выгрузки от числа автомобилей

Приведенному на рис. 3. графику соответствует уравнение:

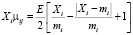. (6)

Подставляя сюда значение Е и производя несложные преобразования, получим:

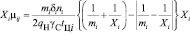.(7)

Тогда интенсивности μ₄₅ и μ₇₈ переходов из состояний погрузки и выгрузки примут вид:

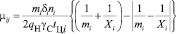. (8)

Однако, поскольку ожидание погрузки и разгрузки мы выделили в отдельные состояния, количество автомобилей в них не будет превышать число постов в этих состояниях, и интенсивности μ₄₅ и μ₇₈ окончательно примут значения:

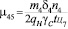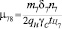; . (9)

Так как на посты погрузки или выгрузки автомобили будут поступать либо по мере освобождения постов (при наличии очереди), либо по мере прибытия в пункт погрузки-выгрузки (при отсутствии очередей в этих состояниях), то суммарные интенсивности переходов автомобилей из состояний ожидания погрузки и выгрузки в данном случае могут быть определены следующим образом:

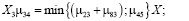
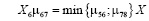. (10)

Интенсивность перехода автомобилей из состояния 1 (в АТП) в состояние 2 (в первом нулевом пробеге) будет зависеть от графика выпуска автомобилей на линию и может быть вычислена по формуле:

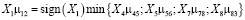, (11)

где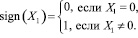

Подставляя полученные значения интенсивностей и вероятностей в систему дифференциальных уравнений перемещения автомобилей по маршруту (3), получим в окончательном виде математическую модель перемещения автомобилей. Процесс непрерывного интегрирования приведенной системы дифференциальных уравнений (3) соответствует процессу последовательного перемещения автомобилей из одного состояния в другое. Точность моделирования при этом определяется величиной выбранного периода интегрирования: чем меньше этот период, тем точнее моделирование.

Одновременно с перемещением автомобилей по маршруту происходит процесс перемещения груза, определяющий выполнение сменно-суточного задания. Математическая модель перемещения груза строится способом, аналогичным тому, что был применен для моделирования перемещения автомобилей [8].

Каждая единица груза может находиться в любой момент времени в одном из шести состояний:

• на складе клиента-поставщика;
• в кузове грузящегося автомобиля;
• в процессе перевозки;
• в кузове автомобиля, ожидающего разгрузки;
• в кузове разгружающегося автомобиля;
• на складе клиента-потребителя.

Реальному процессу перемещения единиц груза в модели будет соответствовать последовательный переход из одного состояния в другое [2]. Граф переходов анализируемой системы представлен на рис. 2. Блоками с двойным контуром обозначены возможные состояния единиц груза, а пунктирными стрелками направления перехода из одного состояния в другое.

На этом графе римскими цифрами обозначены возможные состояния единиц перевозимого груза в соответствии с приведенным перечнем состояний. Через Y_i обозначено количество единиц груза в i-ом состоянии (под состоянием с индексом i = 0 подразумевается любое внешнее по отношению к рассматриваемой системе состояние), через v_ij – интенсивность перехода единицы груза из данного i-го в последующее j-e состояние, а через 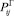– вероятность такого перехода. Отметим, что интенсивности v₀₁ и v₆₀ определяют соответственно скорость поступления груза на склад клиента-поставщика и расходование груза со склада клиента-потребителя; они должны быть заданы в исходных данных. Тогда той части обобщенного графа переходов (рис. 2), которая описывает перемещение единиц груза, можно поставить в соответствие следующую систему из шести дифференциальных уравнений:

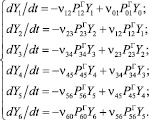(12)

Для возможности совместного решения обоих полученных систем уравнений отметим, что перемещение груза определяется перемещением автомобилей. Произведем следующую замену:

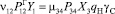
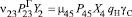
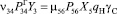(13)

.

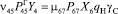
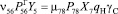Величины 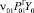и 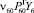аналогичным образом через параметры системы уравнений перемещения автомобилей выражены быть не могут и, как уже отмечалось, должны быть определены в исходных данных. Тогда вторая система уравнений примет следующий вид:

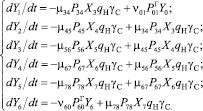(14)

Эти две системы дифференциальных уравнений (3), (15) и составляют основу создаваемой математической модели, а при совместном интегрировании имитируют перемещение по маршруту автомобилей и единиц груза.

Выводы

Предложенная математическая модель хотя и достаточно точна, но обладает рядом существенных недостатков:

• почти не учитывается высокий уровень стохастичности транспортного процесса (данная математическая модель описывает идеальный случай работы маршрута, но имеется возможность варьировать вероятность перехода из одного состояния в другое);
• решение данной модели не приведет к целочисленному результату;
• не учитывается ошибка квантования текущего времени [2].

Поэтому здесь необходимо применять метод имитационного моделирования, сущность которого в последовательной обработке описанных выше состояний с помощью математического аппарата и алгоритмов, реализуемых на ЭВМ.

Рецензенты:

Панов А.Ю., д.т.н., профессор, директор ИПТМ, Нижегородский государственный технический университет им. Р.Е. Алексеева (НГТУ), г. Нижний Новгород;

Молев Ю.И., д.т.н., профессор кафедры «Строительные и дорожные машины» (СДМ), Нижегородский государственный технический университет им. Р.Е. Алексеева (НГТУ), г. Нижний Новгород.

Работа поступила в редакцию 24.06.2014.