Существует большое число работ, в которых приводится определение понятия сложная система [1-2]. Наличие в составе сложной системы технической (технологической) подсистемы (процесса) уточняет определение «сложная система» и выделяет новый класс сложных систем – сложная техническая система (СТС) [3, 4]. Присутствие различных видов неопределенности [5, 6], в которых функционирует СТС, определяет необходимость выделения еще одной разновидности СТС, а именно слабоформализуемых СТС (ССТС), признаки которых введены в [7].
В [8] показано, что для целей анализа ССТС могут быть представлены в виде ориентированного графа, в котором вершины представляют факторы влияния на систему, а ребра показывают направление и влияние одного фактора на другой. Прогнозирование состояния таких систем сводится к определению наиболее сильных влияний, которые затрагивают наибольшее количество важных областей системы, что обеспечивают когнитивные карты [9], значения факторов в них будут меняться прямо пропорционально или обратно пропорционально силе влияния. Однако для целей анализа и моделирования ССТС возможностей когнитивных карт не достаточно, поэтому предлагается применять нечеткие когнитивные карты [10].
По результатам критического анализа различных видов нечетких когнитивных карт предложено использовать для целей моделирования ССТС нечеткие когнитивные карты (НКК) В.Б. Силова [11].
Таким образом, в работе решается актуальная научно-практическая задача разработки среды нечеткого когнитивного моделирования (СНКМ) ССТС. Вопросам разработки подобных сред посвящено значительное число работ. Самая известная в нашей стране система – «Канва» [12].
Методика и теоретические основы построения СНКМ
Наиболее точной моделью для построения НКК считается математическая модель В.Б. Силова. Для данной модели предложено использовать НКК с диапазоном значений для уровня влияния одного концепта на другой: [-1;1].
НКК математической модели В.Б. Силова может быть представлена в виде матрицы смежности, в которой на пересечении строки и столбца указывается уровень влияния одного концепта на другой. Направление влияния определяется на уровне построения когнитивной карты, где необходимо выяснить какой из концептов является причиной, а какой следствием.
Таким образом, по строкам указываются концепты-причины, а по столбцам концепты-следствия. Для работы с такими когнитивными картами была введена каузальная алгебра, которая использует операции T-норм, S-норм, макстриангулярную композицию, операцию max и замыкание. Данная алгебра используется для определения взаимовлияний концептов, а именно нахождения максимального веса пути от концепта wi до концепта wj.
Сложность данной задачи заключается в использовании отрицательных влияний. В качестве концептов в нечеткой когнитивной карте выступают факторы взаимного влияния из диаграммы [8].
Нечеткая когнитивная матрица взаимовлияний будет иметь вид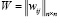 
, где n – число концептов. Перейдем к рассмотрению взаимовлияния концептов, для этого получим нечеткую матрицу положительных обратных связей 
.
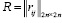После этого формируется транзитивно замкнутая когнитивная матрица взаимовлияний, которая позволяет определить согласованные отношения взаимовлияния концептов.
Для определения влияния концептов друг на друга, а также интегральные показатели влияния концептов на систему и системы на концепты используем консонанс и диссонанс влияния одного концепта на другой, а также консонанс и диссонанс влияния системы на концепт. Для этого используется матрица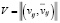 
, полученная из матрицы 
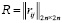по специальному правилу преобразования [10].
Для исследования системных характеристик получим из матрицы 
матрицу 
:
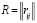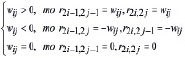(1)
Затем осуществляется транзитивное замыкание матрицы R: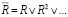 
, однако размерность данной матрицы велика, поэтому в статье ее приводить нецелесообразно. Для исследования динамического влияния компонентов на систему и обратного влияния необходимо получить матрицу 
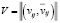с помощью следующего преобразования [10]:
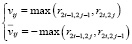(2)
Границы применимости НКК для целей моделирования ССТС
Необходимость очертить границы применимости НКК для технических систем вызвана тем, что методы когнитивного моделирования применяются для слабоструктурированных систем (ситуаций), когда построение аналитической модели затруднено или невозможно. Однако существует ряд задач, например, построение моделей слабоформализуемых технологических процессов (СФТП) [7, 13] и управления данным классом процессов на основе таких моделей [14], когда применение нечеткого когнитивного моделирования позволит существенным образом повысить эффективность управления СФТП. В задачах управления СФТП присутствует структурная неопределенность, для анализа и устранения которой НКК подходят наилучшим образом.
Пример реализации ССТС в СНКМ
В соответствии с методикой, предложенной в [7] и развитой в [8] покажем способ представления ССТС в форме диаграммы взаимного влияния факторов [15], которая легко трансформируется в НКК. Приведенный в [8] пример для выявления влияния различных факторов на активность катализатора в СФТП получения элементарной серы с помощью метода Клауса может быть преобразован в НКК (рис. 1). Приведенный в [8] метод построения диаграмм взаимного влияния факторов может использоваться для получения весов влияния для НКК, однако требует модификации для учета обратного влияния факторов между уровнями представления (рис. 1).
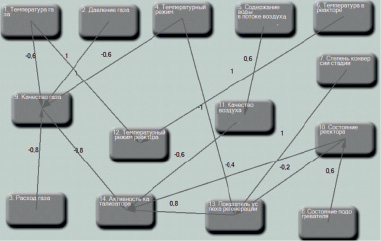
Рис. 1. Представление системы в СНКМ
Полный перечень концептов рассматриваемого примера (рис. 1): температура газа, давление газа; расход газа, температурный режим, содержание воды в потоке воздуха, температура в реакторе; степень конверсии стадии, состояние подогревателя, качество газа, состояние реактора, качество воздуха, температурный режим реактора, показатель успеха регенерации, активность катализатора.
Выбранная шкала взаимовлияний концептов [-1;1] может быть вербально формализована следующим образом: –1 – сильное отрицательное влияние; 0 – влияние отсутствует; 1 – сильное положительное влияние; промежуточные значения в интервале (-1;0) характеризует ослабление степени отрицательного влияния; промежуточные значения в интервале (0;1) характеризует увеличение степени положительного влияния.
Определим согласованные значения отношений причинности в построенной НКК и представим их в виде когнитивной матрицы взаимовлияний. Полученную матрицу ввиду большой размерности (равной 14 х 14) приводить в тексте статьи не целесообразно. Для проведения дальнейшего анализа вычислим интегральные показатели влияния концептов на систему и влияние системы на концепты (таблица).
Интегральные показатели
|
Концепты |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Влияние системы на концепт |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
Влияние концепта на систему |
0.06 |
0.01 |
-0.01 |
-0.17 |
0.02 |
0.07 |
0.13 |
|
Концепты |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
Влияние системы на концепт |
0 |
-0.07 |
0.04 |
0.04 |
0.14 |
-0.02 |
-0.09 |
|
Влияние концепта на систему |
0.02 |
-0.06 |
-0.04 |
-0.04 |
0 |
0.06 |
0 |
Для обеспечения визуализации полученных данных в ходе представления СФТП в виде НКК в СНКМ реализован механизм «Графики» (рис. 2, 3). С помощью данной формы можно получить следующие графики зависимости (по оси абсцисс отложены номера концептов, а по оси ординат уровень влияния из диапазона [-1;1]) [16]: влияние системы на концепты; влияние концептов на систему; консонанс влияния системы на концепты; консонанс влияния концептов на систему; диссонанс влияния системы на концепты; диссонанс влияния концептов на систему.
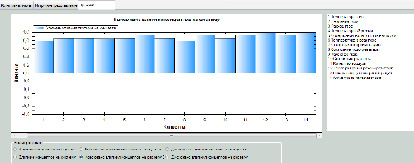
Рис. 2. Окно визуализации показателей в СНКМ (консонанс)
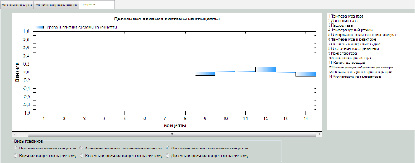
Рис. 3. Окно визуализации показателей в СНКМ (диссонанс)
Полученные графические результаты имитационного моделирования в целом совпадают с результатами, опубликованными в работах [13-14]. Это означает, что применение концептуальных основ метода устранения структурной неопределенности математических моделей СФТП [8] может применяться для построения НКК и получения весов, однако с некоторой модификацией, которая необходима для учета отрицательных весов из диапазона [-1;0).
Заключение
На основании проведенного обзора определений ССТС корректным является предположение о возможности рассмотрения в качестве примера не всей ССТС (в силу сложности и большой размерности задачи), а конкретного СФТП, входящего в ее состав. Пример, рассмотренный в работе, позволяет утверждать, что разработанная СНКМ может быть применима для целей имитационного моделирования ССТС. Показано, что существуют границы применимости НКК для целей моделирования ССТС.
В качестве дальнейшей работы по развитию функциональных возможностей СНКМ предполагается добавление автоматизированного механизма построения обобщенной НКК на основе анализа и объединения НКК нескольких экспертов по аналогии с методом построения моделей СФТП со структурной неопределенностью [8], с учетом механизмов получения весов из диапазона [-1;0).
Рецензенты:
Ханова А.А., д.т.н., доцент, заведующий кафедрой «Прикладная информатика в экономике», ФГБОУ ВПО «Астраханский государственный технический университет», г. Астрахань;
Попов Г.А., д.т.н., профессор, заведующий кафедрой «Информационная безопасность» ФГБОУ ВПО «Астраханский государственный технический университет», г. Астрахань.
Работа поступила в редакцию 24.06.2014.
Библиографическая ссылка
Захарова А.С., Глызин А.А. НЕЧЕТКОЕ КОГНИТИВНОЕ МОДЕЛИРОВАНИЕ СЛАБОФОРМАЛИЗУЕМЫХ СИСТЕМ И ПРОЦЕССОВ // Фундаментальные исследования. – 2014. – № 9-3. – С. 511-515;URL: https://fundamental-research.ru/ru/article/view?id=34877 (дата обращения: 03.12.2024).