Целью работы является выявление закономерностей строения межфазных слоев на границе раздела жидкой и твердой фаз с позиций теории Ван-дер-Ваальса.
Феноменологическая (капиллярная) теория смачивания была разработана Юнгом (1804 г.) и Лапласом (1805 г.). Количественной мерой смачивания служит краевой угол между касательной к искривленной поверхности жидкости и смоченной площадью [5] Классический подход к описанию явлений смачивания подробно изложен в работе [1] (рис. 1 взят из этой работы). Для количественного описания смачивания жидкостью твердого тела рассматривается равновесие сил, действующих на элемент контура, образованного пересечением трех границ раздела фаз: газа 1, жидкости 2 и твердого тела 3 (см. рис. 1).Указанные на рисунке силы образованы поверхностными натяжениями на границах раздела рассматриваемых фаз.Рассмотрение равновесия изображенных на рисунке сил позволяет получить известное уравнение:
cosθ = 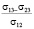 = k, (1)
= k, (1)
где σ12, σ13 и σ23 – поверхностные натяжения на границах раздела газ-жидкость, газ-твердое тело и жидкость-твердое тело. Угол θ носит название краевого угла смачивания, а k – коэффициента смачивания, который может принимать значение – < k < 1.
В критической работе [4] отмечено, что за время существования этого теоретического уравнения не было получено достаточно полного его экспериментального подтверждения. В записанном уравнении только один параметр σ12 может быть экспериментально измерен методами, справедливость которых ставится под сомнение. Два остальных параметра не поддаются прямому измерению, что сводит к нулю практическую значимость уравнения.
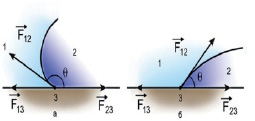
Рис. 1. Схемы к расчету равновесия капли на поверхности твердого тела для случаев несмачивающей (а) и смачивающей (б) жидкостей. 1 – газ; 2 – жидкость; 3 – твердое тело
В работе [2] было высказано предположение о том, что напряжения, формирующие поверхностные натяжения, представляют собой девиаторные компоненты тензора межфазных напряжений. Кроме того, показано, что сумма давления и нормального к разделяющей поверхности напряжения, создаваемого объемными силами, постоянна в каждой точке межфазного слоя и равна давлению в объемной фазе жидкости. Установим, справедливы ли эти закономерности для межфазного слоя жидкость-твердое. Для этого рассмотрим равновесие жидкой капли на твердой поверхности.
Представим каплю жидкости на твердой подложке в виде сферического сегмента, форма которого определяется значением телесного угла φ0, равного краевому углу смачивания. По форме сегмента судят о степени смачивания твердой поверхности жидкостью. Сферическая часть поверхности сегмента представляет собой границу раздела жидкой и газовой фаз, а плоская часть является пятном контакта твердой и жидкой фаз. Вдоль этих поверхностей образуются межфазные слои, по толщине которых происходит глобальное изменение параметров состояния среды, одним из которых является давление.
Найдем соотношение между давлениями, действующими на сферическую и плоскую поверхности, при котором обеспечивается равновесие жидкостного сферического сегмента. Не вдаваясь в детали, будем пока называть напряжения, действующие по поверхности сферического сегмента, давлениями. В рассматриваемой ситуации это название отражает только тот факт, что напряжения перпендикулярны к поверхностям, по которым они действуют. Расчетная схема представлена на рис. 2.
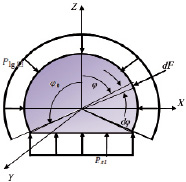
Рис. 2. Схема к расчету равновесия сферического сегмента. Индексы: l – жидкость; g – газ; s – твердое
Обозначим давление на границе раздела жидкой и газовой фаз Plg, а твердой и жидкой фаз – Pls (см. рис. 2). Выделим элемент сферической поверхности, ограниченный углами dφ и dψ. Угол φ лежит в плоскости ZX, а угол ψ – в плоскости, параллельной XY. Площадь элемента будет равна:
dS = 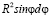 dψ.
dψ.
Значение элементарной силы dF, создаваемой давлением Plg на этой площадке, равно:
dF = 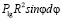 dψ,
dψ,
а ее проекция на ось Z:
dFz = 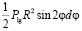 dψ.
dψ.
Интегрируя значение силы по сферической поверхности, получим:
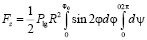 =
= 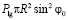 .
.
Вычисляя значение вертикальной силы, действующей на плоскую часть сегмента, получим:
Fz = 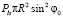 ,
,
Отсюда следует равенство давлений, действующих на сферическую и плоскую поверхности сегмента, т.е. Plg = Pls. Полученный результат на первый взгляд кажется тривиальным, но является основанием для дальнейших рассуждений. Используем прием, рассмотренный в работе [2], о равновесии целого объекта и его части. Его использование позволяет поместить разделительную плоскость, представленную на рисунке, в произвольной точке межфазного слоя жидкость-твердое. Отсюда следует, что равенство Plg = Pls справедливо для каждой точки рассматриваемого межфазного слоя. В работе показано, что в каждой точке межфазного слоя жидкость-газ выполняется условие постоянства нормальных к поверхности слоя напряжений, т.е. σzz = const = Pот1. В рассматриваемом случае в давления вкладывался смысл нормальных напряжений, откуда следуют равенства: σzz = Plg = Pls = Pот1; σzz = Pотм + σzz′. Здесь Pотм – давление в произвольной точке М межфазного слоя, определяемое из уравнения Ван-дер-Ваальса, σzz′ – компонента девиатора напряжений для данной точки.Таким образом, закономерности межфазного слоя жидкость-газ остаются в силе для межфазного слоя жидкость-твердое.
Для иллюстрации механизма формирования девиаторных компонентов тензора напряжений воспользуемся аналогией. Рассмотрим деформацию одноосного растяжения-сжатия твердого образца цилиндрической формы (см. верхнюю строку рис. 3). Действие сжимающего напряжения σzz (рис. 3, а) приводит к искажению формы образца – он принимает бочкообразную форму. При растягивающем напряжении (рис. 3, в) образец принимает форму обратного бочонка.
Напряженное состояние, отвечающее этим схемам, может быть представлено двумя способами со следующими значениями компонент тензора:
1. σzz = σzz; σxx = σyy = 0.
2.σ = 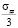 ;
;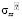 =
= 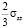 ;
;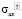 =
= 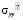 = -
= - 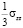
При втором способе записи тензора σ определяет шаровую часть, а компоненты, обозначенные штрихами, составляют девиатор напряжений. Шаровая часть тензора удовлетворяет закону Паскаля и может рассматриваться как давление сил отталкивания в жидкости. Для записи компонент тензора необходимо установить правило знаков. В теории Ван-дер-Ваальса положительными считаются давления сил отталкивания, в то время как в механике сплошных сред положительными принято считать растягивающие напряжения. В дальнейшем будем пользоваться правилом знаков из механики сплошных сред. В соответствии с этим записанные выше компоненты тензора отвечают деформации растяжения, а для деформации сжатия напряжения будут иметь противоположные знаки.
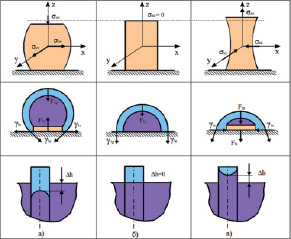
Рис. 3. Схемы формирования поверхностных натяжений и их проявление в капиллярном эффекте: σxx , σyy, σzz – нормальные компоненты тензора напряжений; γij – поверхностное натяжение между i-й и j-й – фазами; Fij – объемная сила между i-й и j-й – фазами
В средней строке рис. 3 показаны схемы межфазных слоев жидкость-газ и жидкость-твердое, в основу которых положено предположение о формировании поверхностных натяжений девиаторными компонентами тензора межфазных напряжений.
Как показано выше, закономерности напряженного состояния среды в межфазном слое жидкость-газ справедливы и для слоя жидкость-твердое. Такое соответствие является вполне закономерным, т.к. в обоих случаях межфазный слой формируется из жидкой фазы, уравнением состояния которой является уравнение Ван-дер-Ваальса. При этом наличие в системе твердой или газовой фазы рассматривается как внешнее воздействие, формирующее межфазный слой.
Таким образом, межфазному слою жидкость-твердое должен отвечать определенный участок изотермы Ван-дер-Ваальса. В работе [3] установлено (может быть, несколько преждевременно) соответствие между точками межфазного слоя и точками изотермы Ван-дер-Ваальса для различных случаев смачивания твердой поверхности. На рис. 3 представлены три случая смачивания твердой поверхности жидкостью.Отметим, что до настоящего времени не принято единой терминологии по степени смачивания твердой поверхности жидкостью. В различных литературных источниках применяют такие термины, как частичное и полное смачивание или несмачивание, ограниченное смачивание и т.п. Для исключения недоразумений в рамках настоящей работы будем использовать такую терминологию по степени возрастания смачивания: полное несмачивание → ограниченное смачивание → равновесное смачивание → частичное смачивание → полное смачивание.
Очевидно, что степень смачивания определяется соотношением между адгезионными (силы притяжения молекул жидкости и твердого) и когезионными (силы молекулярного притяжения в жидкости) силами. Каждому уровню смачивания отвечает определенная точка или участок изотермы Ван-дер-Ваальса, протяженностью которого определяется толщина соответствующего межфазного слоя. Рассмотрим более подробно каждое из состояний в обозначенной схеме.
Полное несмачивание. Краевой угол смачивания θ = π, силы адгезии равны нулю, т.е. отсутствует межмолекулярное взаимодействие жидкой и твердой фаз. Такому состоянию соответствует точка изотермы Ван-дер-Ваальса с минимальным значением давления Р. Межфазному слою отвечает участок изотермы от точки со значением давления P_min до точки Р = 0. Толщина межфазного слоя максимальна и равна толщине слоя жидкость-газ. Во всех остальных случаях смачивания толщина слоя будет определяться положением точки М на изотерме Ван-дер-Ваальса (см. [3]).
Ограниченное смачивание. π > θ 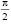 . При ограниченном смачивании точка М межфазного слоя на границе жидкой и твердой фаз располагается на участке изотермы со значениями удельных объемов V2 > VM> V1 (см. рис. 2 в работе [2]). В этом случае когезионные силы больше адгезионных, объемная сила в каждой точке межфазного слоя направлена в сторону объемной фазы жидкости, что эквивалентно дополнительному сжатию межфазного слоя. Толщина межфазного слоя соответствует участку изотермы от точки М до точки с давлением Р на изотерме равным нулю. Этому случаю отвечает рис. 3, а).
. При ограниченном смачивании точка М межфазного слоя на границе жидкой и твердой фаз располагается на участке изотермы со значениями удельных объемов V2 > VM> V1 (см. рис. 2 в работе [2]). В этом случае когезионные силы больше адгезионных, объемная сила в каждой точке межфазного слоя направлена в сторону объемной фазы жидкости, что эквивалентно дополнительному сжатию межфазного слоя. Толщина межфазного слоя соответствует участку изотермы от точки М до точки с давлением Р на изотерме равным нулю. Этому случаю отвечает рис. 3, а).
Равновесное смачивание. θ = 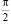 (см. рис. 3, б). Этому случаю смачивания отвечает точка изотермы с координатами: V = V1; Р = 0. Силы адгезии равны силам когезии, в связи с чем, объемной силы не возникает, а твердая фаза не вносит возмущения в жидкость. При этом межфазный слой не формируется, т.е. его толщина равна нулю.
(см. рис. 3, б). Этому случаю смачивания отвечает точка изотермы с координатами: V = V1; Р = 0. Силы адгезии равны силам когезии, в связи с чем, объемной силы не возникает, а твердая фаза не вносит возмущения в жидкость. При этом межфазный слой не формируется, т.е. его толщина равна нулю.
Частичное смачивание. 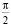 > θ> 0 (рис. 3, в). В этом случае граничная точка между жидкой и твердой фазами располагается на участке изотермы в области значений удельного объема VM < V1. Силы адгезии больше сил когезии, объемная сила направлена в сторону твердой поверхности, а межфазный слой испытывает растягивающее воздействие.
> θ> 0 (рис. 3, в). В этом случае граничная точка между жидкой и твердой фазами располагается на участке изотермы в области значений удельного объема VM < V1. Силы адгезии больше сил когезии, объемная сила направлена в сторону твердой поверхности, а межфазный слой испытывает растягивающее воздействие.
Полное смачивание. θ = 0. Такая ситуация возможна чисто теоретически, а знак строгого равенства в предыдущем выражении, по-видимому, недостижим. В рассматриваемом случае силы когезии должны быть пренебрежительно малы в сравнении с силами адгезии, а ситуация выходит за рамки данного исследования.
Одной из наиболее наглядных демонстраций различных случае всмачивания является возникновение капиллярного эффекта, наблюдаемого в тонких трубках. В нижней строке рис. 3 показано проявление капиллярного эффекта для трех случаев:
а) – ограниченное смачивание;
б) – равновесное смачивание;
в) – частичное смачивание.
Традиционные представления, объясняющие возникновение капиллярного эффекта, весьма туманны. Так, в работе [1] эффект поднятия и опускания уровня жидкости в капилляре в различных случаях смачивания объясняется уменьшением или увеличением давления жидкости в капилляре «по сравнению с внешним». При этом непонятно, о каком внешнем давлении идет речь. Возможно, имеется в виду изменение давления насыщенного пара над искривленной поверхностью жидкости, определяемое уравнением Кельвина.
Однако все объясняется достаточно просто с позиций рассмотренных представлений. Прежде всего необходимо определиться с началом отcчета, т.е. определить уровень жидкости, по отношению к которому отсчитывается давление.Очевидно, что за начало отсчета давлений следует принять уровень жидкости в трубке для случая, показанного на рис. 3, б), когда воздействие твердой поверхности на окружающую ее жидкость отсутствует. Опускание мениска ниже обозначенного уровня означает снижение давления жидкости, а его поднятие – возрастание. Отметим, что речь идет об изменении гидростатического давления в сечении трубки с нулевым уровнем. С учетом того, что точки межфазного слоя при ограниченном смачивании (рис. 3, а) располагаются на изотерме Ван-дер-Ваальса в области давлений, ниже равновесного – мениск опускается. Противоположная картина наблюдается для случая частичного смачивания. Еще раз подчеркнем, что добавление к тензору девиатора напряжений, формирующего поверхностное натяжение, не сказывается на значении давления в рассматриваемой точке изотермы. При этом проявление капиллярного эффекта в конечном счете определяется изменением внутреннего давления жидкости в межфазном слое.
Основным показателем смачивания материала, как указывалось выше, является краевой угол смачивания, косинус которого определяет значение коэффициента смачивания. Проанализируем уравнение (1), приведенное в начале работы. В нем присутствуют три межфазных поверхностных натяжения, из которых только одно поддается прямому измерению. Здесь речь идет о поверхностном натяжении жидкость-газ, методы измерения которого не внушают доверия. Два других поверхностных натяжения являются «вещью в себе». Более того, вызывает сомнение сам факт существования поверхностного натяжения твердое-газ, т.е. σ13 в выражении (1). При любом из рассмотренных уровней смачивания переход от газовой фазы к твердой в соответствии с изотермой Ван-дер-Ваальса должен осуществляться через жидкую фазу. Исключение составляет только случай полного несмачивания, когда граничная точка межфазного слоя жидкость-твердое совпадает с точкой на границе твердой и газовой фаз. Однако такой случай вряд ли может представить практический интерес.
Таким образом, для любого случая смачивания, за исключением одного, переход среды от газовой фазы к твердой должен сопровождаться скачкообразным изменением свойств среды, при котором выбрасывается из рассмотрения целый участок изотермы, отвечающий жидкому состоянию. Такое поведение противоречит начальным посылкам работы, основанным на плавном изменении параметров состояния в соответствии с изотермой Ван-дер-Ваальса. Кроме того, формирование межфазного слоя происходит под действием сил межмолекулярного притяжения, радиус действия которых ограничен. В межфазном слое жидкость-газ толщина слоя равна радиусу дальнодействия сил притяжения в жидкости. Совокупность состояний среды в слое определяется участком изотермы Ван-дер-Ваальса со значениями удельных объемов V2 > V > V1. Протяженность участка изотермы, соответствующего газовой фазе, существенно больше – на нем может уложиться несколько межфазных слоев жидкость-газ. В соответствии с этим механизм межмолекулярного взаимодействия в газовой фазе не может привести к образованию межфазного слоя, аналогичного слою жидкость-газ. С учетом сказанного существование межфазного слоя твердое-газ и поверхностного натяжения, формируемого этим слоем, вызывает серьезные сомнения.
При этом создается впечатление, что межфазная сила F13, изображенная на рис. 1, была введена в классической теории только для того, чтобы замкнуть уравнение равновесия. Подтверждением этогому служит тот факт, что направление межфазной силы F23 остается неизменным независимо от характера смачивания твердой поверхности жидкостью. В соответствии со сказанным, поверхностное натяжение между твердой и газовой фазами может быть исключено из рассмотрения при описании поверхностных явлений. Значение коэффициента смачивания, имеющего традиционный смысл, может быть определено из схем в средней строке рис. 3:
k = cosθ = –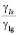 .
.
При вычислении коэффициента смачивания значения поверхностных натяжений должны учитываться в соответствии с используемым правилом знаков (+ – растяжение, – – сжатие).
В заключение отметим, что выдвинутые в работе положения вносят существенные коррективы в традиционные представления теории поверхностных явлений и требуют предоставления серьезных доказательств, подтверждающих их справедливость.
Рецензенты:
Епархин О.М., д.т.н., профессор, директор Ярославского филиала государственного образовательного учреждения высшего профессионального образования «Московский государственный университет путей сообщения», г. Ярославль;
Бачурин В.И., д.ф-м.н., профессор, профессор кафедры Ярославского филиала государственного образовательного учреждения высшего профессионального образования «Московский государственный университет путей сообщения», г. Ярославль;
Виноградова М.Г., д.х.н., профессор, профессор кафедры естественнонаучных дисциплин, Тверской институт экологии и права, г. Тверь.
Работа поступила в редакцию 10.06.2014.
Библиографическая ссылка
Готовцев В.М., Румянцев А.Н. МЕХАНИЗМ РАСТЕКАНИЯ ЖИДКОСТИ ПО ТВЕРДОЙ ПОВЕРХНОСТИ // Фундаментальные исследования. 2014. № 9-2. С. 312-317;URL: https://fundamental-research.ru/ru/article/view?id=34845 (дата обращения: 01.03.2026).



