Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Никульчев Е.В. 1 Паяин С.В. 1 Питиков Д.А. 1 Плужник Е.В. 1

---

1 НОУ ВПО «Московский технологический институт «ВТУ»

В настоящее время развитие телекоммуникационных технологий определяет рост исследований в области поиска новых решений и инновационных подходов к математическому описанию процессов. Одним из направлений в области описания трафика в компьютерных сетях являются динамические модели, которые позволяют описать процессы передачи информации в реальном времени в форме дифференциальных или конечно-разностных уравнений. Часть этих исследований посвящена изучению хаотических свойств трафика. В первой части показывается невозможность построения динамических моделей на основе теории массового обслуживания, в связи с невыполнением требований к распределению случайной величины. Во второй части приведены результаты по определению характеристик динамического хаоса. Показано, что оценка знака старшего показателя Ляпунова не гарантирует хаотичность динамики. Предложено ввести дополнительные показатели, основанные на отсутствии тривиальных законов сохранения и слабом нарушении симметрий. Сделан вывод о наличии динамического хаоса в исследуемом трафике компьютерной сети.

Статья в формате PDF

535 KB

трафик компьютерных сетей

показатели Ляпунова

инвариантные характеристики

модели трафика

динамический хаос

1. Карпухин А.В., Ткаченко А.А. Моделирование хаотических явлений в инфокоммуникационных сетях: синергетический подход // Проблемы телекоммуникаций. – 2013. – № 3 (12). – С. 36–52.

2. Купцов П.В. Вычисление показателей Ляпунова для распределённых систем: преимущества и недостатки различных численных методов // Известия вузов. Прикладная и нелинейная динамика. – 2010. – Т. 18. – № 5. – С. 93–112.

3. Никульчев Е.В. Паяин С.В., Плужник Е.В. Динамическое управление трафиком программно-конфигурируемых сетей в облачной инфраструктуре // Вестник Рязанского радиотехнического университета. – 2013. – № 3. – C. 54–57.

4. Никульчев Е.В. Моделирование и идентификация динамически-сложных систем на основе группового анализа // Мехатроника, автоматизация, управление. – 2004. – № 10. – С. 2–7.

5. Никульчев Е.В. Геометрический подход к моделированию нелинейных систем по экспериментальным данным: монография. – М.: МГУП, 2007.

6. Питиков Д.А., Никульчев Е.В., Паяин С.В. Разработка динамической системы диагностирования компьютерных сетей на основе оценки инвариантных характеристик // Труды НГТУ им. Р.Е. Алексеева. – 2009. – Т. 76. – № 16. – С. 103–106.

7. Chossat P., Golubitsky M. Symmetry-increasing bifurcation of chaotic attractors // Physica D: Nonlinear Phenomena. – 1988. – Т. 32. – № . 3. – С. 423–436.

8. Liu Z. Chaotic Time Series Analysis // Mathematical Problems in Engineering. – 2010. – Vol. 2010.– 31 с. (doi:10.1155/2010/720190)

9. Pluzhnik E.V., Nikulchev E.V. Use of dynamical systems modeling to hybrid cloud database // International Journal of Communications, Network and System Sciences.– 2013.– Vol. 6.– № 12.– P. 505–512. (doi: 10.4236/ijcns.2013.612054)

10. Nikulchev E.V., Kozlov O.V. Identification of Structural Model for Chaotic Systems // Journal of Modern Physics. – 2013. – Vol. 4. – № 10. – рр. 1381–1392. (doi: 10.4236/jmp.2013.410166)

11. Xiong W., Hu H., Xiong N., Yang L.T., Peng, W.C., Wang X., Qu Y. Anomaly secure detection methods by analyzing dynamic characteristics of the network traffic in cloud communications // Information Sciences. – 2014. – Vol. 258. – P. 403–415. (doi: 10.1016/j.ins.2013.04.009).

Статья посвящена вычислению инвариантных характеристик динамического хаоса на основе трафика корпоративной компьютерной сети.

Значительное количество работ по моделированию трафика в компьютерных сетях основывается на теории массового обслуживания. При этом, естественно, применяется гипотеза о пуассоновском потоке, но эта гипотеза часто не подтверждается практикой. Гипотеза о пуассоновских потоках может быть применена в сетях с большой избыточностью по ширине каналов, в остальных случаях имеют место другие виды распределения и требуются принципиально другие подходы к моделированию.

Для современных сетей, характеризующихся распределенностью вычислительных ресурсов и разнообразием конечных пользователей (от гаджетов до бытовых приборов, имеющих выход в интернет), моделирование с целью создания систем управления коммуникационными каналами является особенно актуальной задачей.

1. Исследование вида распределения

Основой для анализа служили данные о загрузке интернет-канала, полученные в ходе мониторинга работы вузовской корпоративной сети, измеренные в течение года. Статистика получена при снятии информации с интерфейсов маршрутизатора о количестве переданной информации и загрузке порта, по протоколу snmp, при использовании пакета Paessler Router Traffic Grapher, который формирует таблицы с данными и графики загрузки (рис. 1).

Эмпирическая гистограмма частот загрузки канала приведена на рис. 2. На основе использования критериев согласия Пирсона и Колмогорова – Смирнова наблюдаемое распределение вероятностей не согласуется с распределением Пуассона. Эмпирическая гистограмма имеет «тяжеловесный хвост», свидетельствующий о наличии пиковых моментов загрузки сети, в которые происходит сильное увеличение задержек и потеря пакетов.

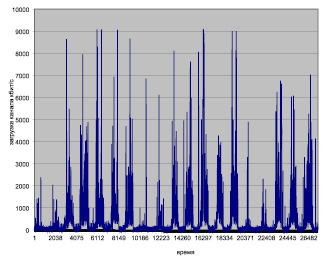
Рис. 1. Фрагмент загрузки канала (20 дней)

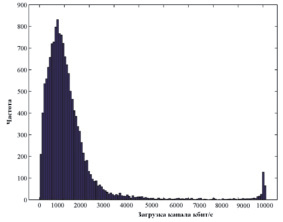
Рис. 2. Эмпирическая гистограмма загрузки выходного канала сети

Информация о загрузке каналов связи была также получена при мониторинге внешних каналов связи одной из компаний-провайдеров и компании по оптимизации сайтов. Полученные гистограммы также обладают тяжеловесными хвостами (рис. 3, а, б), свидетельствующими о наличии пиковых моментов загрузки сети, в которые происходит сильное увеличение задержек и потеря информации.

В связи с тем, что функция распределения имеет тяжеловесный хвост и не согласуется с распределением Пуассона, теория массового обслуживания для рассматриваемых сетей не может обеспечить адекватное математическое описание.

Как отмечается в [1], для протокола TCP/IP распределение с тяжеловесными хвостами вносит основной вклад в самоподобную природу трафика и, следовательно, хаотический характер динамики.

Исследованию хаотичности трафика посвящено ряд работ. В [1] проведены оценки значений старшего показателя Ляпунова на основе трафика, генерируемого на экспериментальном стенде; в [7] Интернет-трафик являлся примером для расчета различных характеристик; в [3, 8] использовались динамические свойства хаоса для решения телекоммуникационных задач обмена данных, однако исследование хаотических свойств оставалось за рамками публикаций.

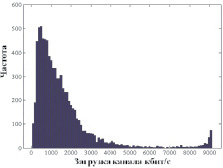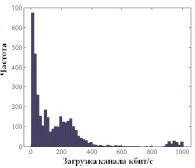а б

Рис. 3. Эмпирическая функция распределения загрузки каналов корпоративных сетей

2. Вычисление характеристик динамического хаоса

Предполагается, что временной ряд порожден дискретной

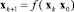(1)

или непрерывной системой

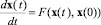(2)

Здесь x = (x₁(t), ..., x_n(t)); n – размерность фазового пространства; t – время; k – дискретное время (номер); F, f – вектор функции. Фазовой траекторией непрерывной системы является n-мерная кривая, представляющая собой решение системы в координатах пространства состояний при заданных начальных условиях x0. Для дискретных систем состояния соединятся линиями в соответствии с последовательностью отсчетов k = 1, 2, …

Важным понятием динамических систем является аттрактор. Для систем, находящихся в положении равновесия, аттрактор представляет собой точку (с изменением времени состояния x не меняется), для колебательных систем – замкнутые траектории (циклы). Для хаотических систем существует аттрактор, который называется странным, в этом случае траектории стягиваются, но не в точку, кривую, тор, а в некоторое подмножество фазового пространства. Аттрактор является инвариантной характеристикой системы, т. е. сохраняется при действиях преобразований.

Однозначными характеристиками хаотичности сигнала является спектр показателей Ляпунова. Положительный максимальный показатель Ляпунова является показателем хаотической динамики, нулевой максимальный показатель Ляпунова обозначает предельный цикл или квазипериодическую орбиту и отрицательный максимальный показатель Ляпунова представляет собой неподвижную точку [7]. Система размерности n имеет n показателей Ляпунова: λ₁, λ₂, ..., λ_n, упорядоченных по убыванию. По определению, введенному Ляпуновым:

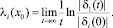
Здесь {δ_i(t)} – фундаментальные решения системы, линеаризованной в окрестности x₀.

Динамические системы, для которых n-мерный фазовый объем уменьшается, называются диссипативными. Если фазовый объем сохраняется, то такие системы носят название консервативных. У консервативных систем всегда существует хотя бы один закон сохранения. Наличие закона сохранения часто влечет существование соответствующего ему нулевого показателя Ляпунова. Для диссипативных динамических систем сумма показателей Ляпунова всегда отрицательна. У диссипативных систем показатели Ляпунова инвариантны относительно всех начальных условий.

По показателям Ляпунова можно многое сказать о динамической системе, о наблюдаемом режиме, о размерности аттрактора, если таковой имеется, и об энтропии динамической системы. Динамическому хаосу отвечает неустойчивость каждой отдельной траектории, т.е. наличие хотя бы одного положительного показателя Ляпунова. Притяжение к аттрактору требует, чтобы фазовые объемы больших размерностей сжимались, то и отражено в ляпуновском спектре. Знание показателей Ляпунова позволяет оценить и фрактальную размерность аттрактора [5].

Тем не менее количество независимых частот можно выяснить не всегда, так как нулевые показатели могут быть связаны и с наличием сохраняющихся величин. Для диссипативных систем наличие законов сохранения, вообще говоря, нетипично, однако соответствующие примеры существуют.

Существует значительное количество численных методов вычисления показателей Ляпунова по временному ряду [5]. Важно, что в условия, что исследуемый ряд порожден системой (1) или (2), старший показатель может быть вычислен. Однако нельзя оценить весь спектр. А для распределенных систем, даже зная систему уравнений, оценка показателя Ляпунова представляет собой существенные вычислительные сложности [2].

Для исследуемого ряда, приведенного на рис. 1, 2, вычислим старший показатель Ляпунова. Для вычислений использовалась система TISEAN. Результаты вычислений различными методами показали положительное значение старшего показателя.

Однако положительность старшего показателя Ляпунова не может являться необходимым условием существования хаоса. Например, даже в системе Лоренца, при положительности старшего показателя, как известно, при ряде условий, имеет место предельный цикл.

В качестве дополнительного критерия предлагается использовать свойство отсутствия тривиальных законов сохранения (симметрий трансляции, растяжения и сжатия). Заметим, что сжатие фазового объема не означает преобразование сжатия.

Для проверки наличия преобразований фрагментов траекторий разработан генетический алгоритм и программа для MATLAB, описание которой изложено в [9]. Одновременно происходит проверка следующего предположения [4, 6] – система допускает преобразования, в условиях слабого нарушения симметрии, т.е. существует некоторая малая величина, незначительно отклоняющая от симметричного отображения. Наглядно, геометрически это видно при почти похожих петлях на аттракторе. Очевидно, что при такой проверке, при разных начальных условиях, для систем с регулярной динамикой будет выявлено наличие тождественной симметрии, для более сложной, но не хаотической – трансляции (сдвига фазового портрета), для систем, стремящихся к устойчивому положению равновесия – сжатие и пр., а для хаоса – почти повторяющиеся участки фазовых траекторий.

Реконструированный, по данным загрузки трафика, аттрактор приведен на рис. 4.

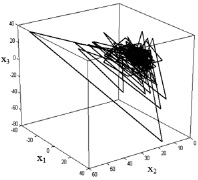
Рис. 4. Аттрактор, построенный на основании трафика сети

Подтверждение хаоса может являться основанием для построения динамических моделей. Например, в форме ансамбля маятников [1], аффинных систем с управлением [5] или в форме рядов.

Заключение

В работе рассмотрены хаотические явления в компьютерных сетях передачи данных. На основании хаотических свойств могут быть построены математические модели динамического поведения трафика. Модели могут быть использованы для обеспечения гарантированного качества обслуживания (QoS) [3], анализа узких мест в структуре корпоративной сети [1], обмена данных в облачных инфраструктурах [8].

В то же время и сами показатели хаоса, структура аттрактора может иметь практическую ценность. Изменение значений старшего показателя Ляпунова, изменение топологии аттрактор, является показателем изменения сетевой активности. Например, компьютерные атаки [6, 10], сбой (отказ в обслуживании) корпоративных систем обмена данных или являться основанием для смены политики администрирования – расширением каналов связи или пополнением списка запрещенных сетевых ресурсов. Последнее наблюдалось, например, с ростом популярности социальных сетей, ресурсов обмена видеоданных.

Рецензенты:

Горяшко А.П., д.т.н., профессор кафедры информатики и автоматизации, НОУ ВПО «Московский технологический институт «ВТУ», г. Москва;

Бубнов Г.Г., д.э.н., профессор, ректор, НОУ ВПО «Московский технологический институт «ВТУ», г. Москва.

Работа поступила в редакцию 04.06.2014.

Библиографическая ссылка