Проблемы и задачи разложения газогидратов в настоящее время представляют значительный научный и практический интерес, что обусловлено широким распространением газогидратных месторождений в природе и перспективами их использования в качестве источников природного газа [1,3].
Математическая модель процесса разложения газогидрата в пористой среде без учета конвективного переноса тепла построена в работах [2,6,7]. Некоторые особенности процесса образования газогидрата в пористой среде рассмотрены в работах [4,5,8,10]. Математическая модель диссоциации газа в пористой среде при инжекции теплого газа представлена в работе [9]. В настоящей работе представлено решение задачи о диссоциации газогидрата в пористой среде при депрессионном воздействии с учетом конвективного переноса тепла.
Основные уравнения
Для описания процессов тепломассопереноса в пористой среде примем следующие допущения. Процесс однотемпературный, т.е. температуры пористой среды и насыщающего вещества (газа, гидрата или воды) совпадают. Гидрат является двухкомпонентной системой с массовой концентрацией газа G. Кроме того, скелет пористой среды, газогидрат и вода несжимаемы и неподвижны, пористость постоянна, газ является калорически совершенным. В рамках отмеченных допущений запишем для плоскоодномерной задачи уравнения сохранения массы, закон Дарси, уравнения состояния газа и притока тепла (без учета баротермического эффекта):
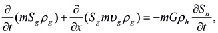
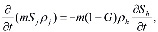
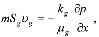 (1)
(1)
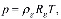
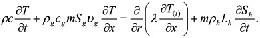
Здесь m – пористость; p – давление, T – температура; ρj и Sj – истинная плотность и насыщенность пор j–й фазы (j = h, l, g); индексы h, l и g относятся к параметрам гидрата, воды и газа соответственно; 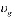 ,
, 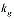 и
и 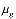 – скорость, проницаемость и динамическая вязкость для газовой фазы; Lh – удельная теплота разложения гидрата; cg – удельная теплоемкость газа; ρc и λ – удельная объемная теплоемкость и коэффициент теплопроводности системы.
– скорость, проницаемость и динамическая вязкость для газовой фазы; Lh – удельная теплота разложения гидрата; cg – удельная теплоемкость газа; ρc и λ – удельная объемная теплоемкость и коэффициент теплопроводности системы.
Зависимость коэффициента проницаемости для газа kg от газонасыщенности можно задать на основе формулы Козени:
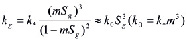
Значения температуры и давления в области разложения гидрата связаны условием фазового равновесия [1]:
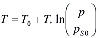 , (2)
, (2)
где T0 – исходная температура системы; ps0 – равновесное давление, соответствующее исходной температуре; T* – эмпирический параметр, зависящий от вида газогидрата.
При диссоциации газогидрата в общем случае могут возникнуть три характерные области. В первой области, находящейся вблизи скважины, поры заполнены газом и водой. Во второй (промежуточной) области происходит разложение газогидрата, поэтому здесь поры заполнены газом, водой и гидратом. В третьей (дальней) области присутствуют газ и гидрат. На границах этих областей должны выполняться условия баланса массы и тепла:
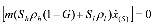 ,
,
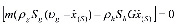 , (3)
, (3)
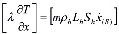 .
.
Здесь 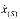 – скорость движения этой границы. Температуру и давление на этой границе будем полагать непрерывными.
– скорость движения этой границы. Температуру и давление на этой границе будем полагать непрерывными.
Будем полагать, что полубесконечный пористый пласт в начальный момент времени насыщен газом и гидратом, давление p0 и температура T0 которых в исходном состоянии соответствуют термодинамическим условиям стабильного существования гидрата (p0>ps0) и изначально одинаковы во всем пласте. Эти условия могут быть записаны следующим образом:
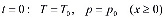 .
.
Пусть через границу пласта отбирается газ и одновременно производится нагрев так, что давление и температура поддерживаются на этой границе постоянными:
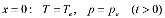 .
.
Аналитическое решение
Сформулированная задача имеет автомодельное решение. Рассмотрим решение с фронтальной поверхностью разложения гидратов. В данном случае возникают две характерные области. В первой области, находящейся вблизи границы пласта, гидрат полностью диссоциировал, поэтому в порах присутствуют только газ и вода. Во второй (дальней) области поры пласта заполнены газом и гидратом. Таким образом, в данном случае разложение газогидрата полностью происходит на фронтальной поверхности между этими областями, а промежуточная область отсутствует.
В автомодельных переменных решение для распределения давления (после применения метода линеаризации Лейбензона) и температуры в каждой из областей может быть записано в виде:
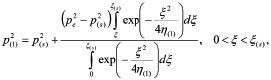
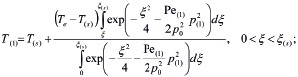 (4)
(4)
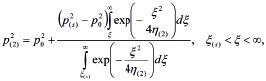
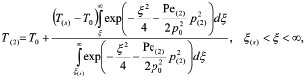 (5)
(5)
где 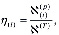
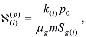
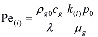 .
.
Параметры первой и второй областей снабжены нижними индексами в скобках i = 1, 2.
На поверхности, разделяющей ближнюю и дальнюю области, происходит скачок гидратонасыщенности от 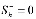 до
до 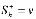 , где v – исходная гидратонасыщенность пласта.
, где v – исходная гидратонасыщенность пласта.
Для значений температуры и давления на границе между областями выполняется условие фазового равновесия (2).
На основе решений (4), (5) и условий баланса массы и тепла на фронтальной границе разложения гидрата (3) получена система трансцендентных уравнений, исходя из которой численно определяются автомодельная координата 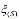 данной границы и значения параметров
данной границы и значения параметров 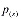 и
и 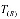 на ней.
на ней.
Полученные решения исследованы на условие термодинамической непротиворечивости, которое состоит в том, что локальная температура в первой (ближней) области должна быть выше локальной температуры разложения гидрата, вычисляемой по найденному в процессе решения распределению давления. Соответственно, температура во второй (дальней) области должна быть ниже данной равновесной температуры.
Результаты расчетов
На рис. 1 приведены распределения температуры и давления для разных значений давления, под которым метан откачивается из пласта. Для параметров, характеризующих систему, приняты следующие значения: m = 0.1, G = 0.12, Si0 = 0.2, p0 = 7 МПа, T0 = 280 К, T* = 10 К, ps0 = 5.5МПа, k0 = 10-14 м2, Rg = 520Дж/(К∙кг), ph = 900 кг/ м3, pl = 1000 кг/ м3, cg = 1560 Дж/(К·кг), pc = 2.5∙10-14 Дж/(К∙кг), λ = 2Вт/(м∙К), μn = 10-5 кг/(м∙с), Lh = 5·105 Дж/кг. Штриховая линия 2 показывает равновесную температуру, соответствующую вычисленному распределению давления. Рисунок показывает, что при небольшом значении депрессии (случай a) температура пласта перед фронтом диссоциации гидрата (т.е. со стороны первой области) выше равновесной температуры, а за фронтом – ниже этой температуры. Следовательно, в этом случае решение с фронтальной поверхностью образования гидрата является непротиворечивым. При более высокой величине депрессии (случай b) температура пласта за фронтом разложения гидрата (т.е. со стороны второй области) поднимается выше равновесной температуры, что соответствует перегреву гетерогенной смеси газа и гидрата в этой области. Следовательно, в этом случае модель с фронтальной поверхностью диссоциации гидрата не позволяет построить физически непротиворечивое решение. Для устранения этого противоречия необходимо вводить объемную область разложения гидрата.
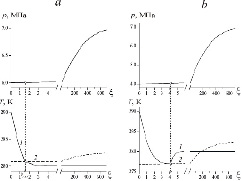
Рис. 1. Распределение давления, температуры пласта (1) и равновесной температуры (2); pe = 6 МПа (a) и pe = 4 МПа (b)
Для определения критического значения давления на границе пласта p*, ниже которого возникает объемная область разложения гидрата, были проведены вычислительные эксперименты в широком диапазоне параметров. На рис. 2 приведены зависимости величины критического давления от абсолютной проницаемости пласта при разных значениях исходной температуры и давления в пласте. Штриховые линии, параллельные оси абсцисс и являющиеся горизонтальными асимптотами сплошных кривых, показывают равновесные давления pso, соответствующие исходным температурам пласта. Графики показывают, что для высокопроницаемой пористой среды значение критического давления практически совпадает со значением равновесного давления, соответствующего исходной температуре пласта. При уменьшении проницаемости величина критического давления снижается, причем тем быстрее, чем ниже исходная пластовая температура и чем выше исходное пластовое давление. Следоваельно, фронтальный режим реализуется в низкопроницаемых пористых средах, а также в низкотемпературных пластах с высоким пластовым давлением, т.е. в пластах, исходное состояние гидрата в которых далеко от условий его разложения.
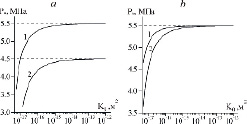
Рис. 2. Зависимость критического значения давления на границе пласта от абсолютной проницаемости пласта при разных значениях: a – начальной температуры пласта: T0 = 280 К (1) и 278 К (2); b – начального давления в пласте: p0 = 6 МПа (1) и 8 МПа (2)
Выводы
Основываясь на проведенных численных расчетах, можно сделать вывод о том, что при отборе газа возможны два принципиально различных режима разложения гидрата. Для величины давления на границе пласта существует некоторое предельное значение, зависящее прежде всего от проницаемости и исходной температуры, ниже которого необходимо рассматривать объемную область разложения гидрата. Для значений проницаемости, характерных для реальных пластов 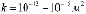 и высокопроницаемых пористых сред, величина этого предельного давления с высокой степенью точности совпадает с величиной равновесного давления ps0, соответствующего исходной температуре.
и высокопроницаемых пористых сред, величина этого предельного давления с высокой степенью точности совпадает с величиной равновесного давления ps0, соответствующего исходной температуре.
Работа поддержана грантом Российского фонда фундаментальных исследований.
Рецензенты:
Мустафина С.А., д.ф.-м.н., профессор, декан физико-математического факультета Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак;
Михайлов П.Н., д.ф.-м.н., профессор, заведующий кафедрой «Алгебра, геометрия и методика обучения математике» Стерлитамакского филиала Башкирского государственного университета, г. Стерлитамак.
Работа поступила в редакцию 04.06.2014.
Библиографическая ссылка
Хасанов М.К., Доровская М.С. ДИНАМИКА ДИССОЦИАЦИИ ГАЗОГИДРАТА В ПОРИСТОЙ СРЕДЕ ПРИ ОТБОРЕ ГАЗА // Фундаментальные исследования. 2014. № 9-1. С. 59-63;URL: https://fundamental-research.ru/ru/article/view?id=34642 (дата обращения: 14.02.2026).



