Эффективное решение задач, связанных с проектированием технологии в процессах обработки металлов давлением (ОМД), требует проведения дорогостоящего экспериментального исследования, вместо которого часто прибегают к имитационному моделированию. В силу высокой достоверности результатов и возможности решения ряда сопутствующих задач наиболее эффективным средством моделирования формоизменения является метод конечных элементов (МКЭ). Широкое внедрение в практику анализа конечно-элементной технологии привело к появлению соответствующих пакетов прикладных программ; в задачах моделирования пластического формоизменения таковыми являются DEFORM, QForm, Simufact.forming и ряд других. Несмотря на наличие профессиональных инструментов, исследования в данной области по-прежнему актуальны в связи с высокой стоимостью и малой доступностью существующего программного обеспечения, закрытостью применяемого математического аппарата и невозможностью моделирования в ситуациях, требующих специального описания граничных условий.
Применение МКЭ требует построения «сетки» элементов – топологического множества точек (также используются термины «узел» и «вершина»), связанных между собой ребрами – отрезками прямых или кривых линий таким образом, что исходная дву- или трехмерная область разбивается на элементы заданной формы. В качестве элементов сетки чаще всего используются геометрические симплексы – треугольники в двумерном и тетраэдры в трехмерном случае. А сам процесс построения сетки принято называть дискретизацией, или триангуляцией. Как указано в работе [2], в настоящее время двумерная триангуляция без адаптации к конкретной предметной области считается решенной проблемой. Актуальными остаются исследования, ориентированные на формирование сеток в специфических условиях. Одной из таких областей является моделирование пластического формоизменения, при котором возникают значительные градиенты скоростей деформации и температур, а деформируемая заготовка принимает сложную форму. Из всего многообразия методов для дискретизации сложных областей наиболее предпочтительными являются два класса – это методы на основе критерия Делоне и методы исчерпывания.
Методы на основе критерия Делоне основаны на формировании триангуляции по существующему множеству опорных точек, которые становятся узлами сетки [4]. Триангуляция Делоне на плоскости – это множество непересекающихся треугольников, в котором ни одна вершина, не принадлежащая данному треугольнику, не попадает в описанную вокруг этого треугольника окружность [7]. В двумерном случае этот подход является наиболее популярным [3], поскольку позволяет эффективно создавать высококачественные сетки. Однако его применение требует рационального решения сложной задачи первичного разбиения – построения множества опорных точек.
Сущность методов исчерпывания заключается в последовательном исключении элементов из заданной области до тех пор, пока вся область не будет исчерпана [2]. В англоязычной литературе данный подход принято называть «advancing front» – продвигающийся фронт, что полностью соответствует идее метода. Исходными данными метода на любой итерации является «фронт» – граница еще не исчерпанной части области. На каждой итерации изымается один или более элемент, после чего «фронт» обновляется, и производится следующая итерация. Идея методов исчерпывания была предложена и развита в конце 80-х годов прошлого века в работах Дж. Перейры, К. Моргана, С.Х. Ло, Р. Лонера и др. Подобные алгоритмы разрабатывались и отечественными учеными [1, 4]. Относительно недавно И.А. Щегловым [6] были предложены алгоритмы «от угла» и «от ребра», позволяющие дискретизировать дву- и трехмерные области сложной формы. Данная работа посвящена адаптации и уточнению алгоритма «от угла» для построения триангуляции двумерной области в задачах моделирования пластического формоизменения, поскольку он в исходном варианте не позволяет генерировать качественную сетку для рассматриваемых областей.
Рассмотрим основные требования, предъявляемые к алгоритму триангуляции при решении задач моделирования пластической деформации:
- сетка должна обеспечивать перемещение элементов вдоль границы инструмента, в том числе на участках с изменением направления течения металла, где на каждом элементе границы должно находиться несколько узлов сетки;
- сетка должна строиться в сложных для затекания металла участках (например, в облойной канавке при горячей штамповке);
- сетка должна иметь возможность сгущения в областях с высокими градиентами скоростей деформации;
- форма элементов должна стремиться к правильной (равносторонний треугольник) для повышения стабильности расчетов;
- плотность сетки должна быть контролируемой, т.е. пользователь должен иметь возможность увеличить количество элементов, если это позволяют вычислительные возможности, но сетка всегда должна оставаться качественной.
Блок–схема предлагаемого алгоритма приведена на рис. 1. Рассмотрим основные его этапы. Исходной информацией для построения триангуляции является кусочно–линейная кривая, охватывающая заполняемую треугольниками область. В нашем случае она формируется как сечение трехмерной модели заготовки на разных этапах деформации, импортируемой из САПР КОМПАС–3D (блок 1) [5].
Для контроля плотности сетки необходимо определить желаемый размер элементов сетки, а точнее среднюю длину ребра (длину стороны треугольника); эту величину принято называть шагом триангуляции (блок 2). С точки зрения пользователя удобнее задавать не размеры элементов, а их количество. Использование итерационного метода с возможностью сгущения сетки не позволяет заранее спрогнозировать количество элементов. Можно рассчитать верхнее значение глобального шага триангуляции исходя из заданного количества элементов и площади деформируемой заготовки с учетом правильной формы элемента:
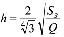 ,
,
где h – шаг триангуляции; S3 – площадь сечения заготовки; Q – заданное количество элементов. Рассчитанная таким образом величина является ориентировочной и корректируется алгоритмом в зависимости от сложности участка области, в котором производится построение элемента, что ведет к увеличению количества элементов относительно указанного пользователем.
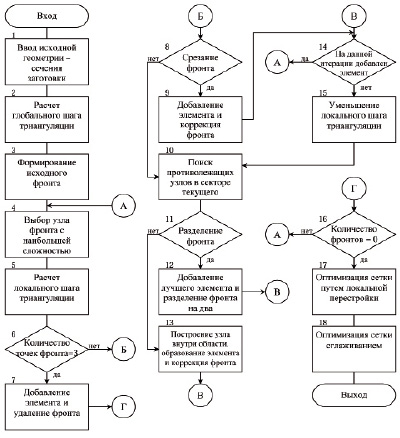
Рис. 1. Блок-схема алгоритма двумерной триангуляции методом исчерпывания
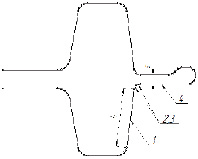
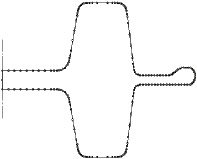
Основным понятием алгоритмов исчерпывания является фронт, который представляется замкнутой последовательностью узлов. Первоначально фронт формируется на основе кусочно-линейной границы, являющейся сечением деформируемой заготовки, исходя из шага триангуляции и дополнительных условий (блок 3). В ходе триангуляции фронт постепенно сжимается вокруг незаполненной части области, при этом может происходить его разделение на два и большее количество фронтов. Узлы начального фронта в дальнейшем становятся узлами элементов и должны быть найдены так, чтобы максимально соответствовать решаемой задаче. При моделировании пластического формоизменения целесообразно исходить из условия, что на каждом отрезке кусочно-линейной границы должно находиться минимум 2 элемента сетки, кроме того, следует уменьшить размеры элементов в участках сложной формы, таких, как облой и радиусы закругления. С этой целью для каждого отрезка i границы рассчитывается делитель ni, определяющий шаг узлов mi=li/ni. При расчете делителя учитывается длина отрезка li , шаг триангуляции h и расстояние до ближайших линий границы в направлении, ортогональном каждому отрезку границы s. На рис. 2, а показано кусочно-линейное представление границы деформируемой заготовки, а на рис. 2, б – узлы исходного фронта для той же области.
|
а) |
б) |
|
Рис. 2. Кусочно-линейная граница (а) и исходный фронт триангуляции (б) |
|
Здесь для отрезка 1 нет дополнительных ограничений, и делитель определяется как округленное до целого числа отношение его длины к шагу триангуляции: 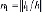 . В случае коротких отрезков 2 и 3 с длиной менее шага триангуляции n 2,3< h выбирается минимальный делитель: n 2,3< 2. На отрезке 4 ограничивающим фактором является малое расстояние до противолежащего элемента, и делитель рассчитывается так, чтобы в данном участке размещались три слоя элементов:
. В случае коротких отрезков 2 и 3 с длиной менее шага триангуляции n 2,3< h выбирается минимальный делитель: n 2,3< 2. На отрезке 4 ограничивающим фактором является малое расстояние до противолежащего элемента, и делитель рассчитывается так, чтобы в данном участке размещались три слоя элементов: 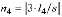 . Для исключения ситуации с резким изменением размеров соседних элементов на внешней границе области, ведущей к появлению очень узких треугольников (например, на стыке отрезков 1 и 2), производится сглаживание фронта, заключающееся во вставке дополнительных узлов между уже существующими: если расстояние от любого узла до двух соседних отличается более чем в 2 раза, то больший отрезок делится пополам путем вставки дополнительного узла.
. Для исключения ситуации с резким изменением размеров соседних элементов на внешней границе области, ведущей к появлению очень узких треугольников (например, на стыке отрезков 1 и 2), производится сглаживание фронта, заключающееся во вставке дополнительных узлов между уже существующими: если расстояние от любого узла до двух соседних отличается более чем в 2 раза, то больший отрезок делится пополам путем вставки дополнительного узла.
Участок алгоритма с 4 по 16 блоки является его основным циклом. Построение элементов сетки начинается с выбора самого сложного участка среди всех фронтов (блок 4), для чего в каждом узле фронта Ni производится расчет сложности Ci по формуле
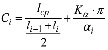 ,
,
где lcp – среднее расстояние между узлами фронта; li-1, li – длины отрезков фронта, прилегающих к узлу Ni (рис. 3); Ka=2 – весовой коэффициент значимости угловой составляющей сложности; ai – угол между отрезками li-1, li . Данный выбор узлов производится только среди узлов с углом ai < p. Согласно этой формуле при близких значениях длин ребер большую сложность будут иметь узлы с малыми углами.
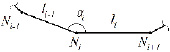
Рис. 3. Участок фронта с узлом Ni
Следующим этапом является определение локального шага триангуляции в выбранном узле (блок 5), который рассчитывается по формуле:
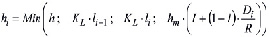 ,
,
где KL=1,35 – коэффициент максимального удлинения стороны элемента, позволяющий получать элементы с незначительным искажением; I – интенсивность сгущения сетки (0,2 ≤ I < 1); R – радиус области сгущения; Di – расстояние от узла до точки сгущения. Последний компонент рассматривается только при нахождении узла Ni в области сгущения Di <R. Использование локального шага триангуляции позволяет формировать сетки со сгущениями на сложных участках границы и в местах с высокими градиентами интенсивностей скоростей деформации, которые обладают достаточно высоким качеством.
Дальнейшая часть алгоритма представляет собой разбор возможных ситуаций, учитывающий значение угла в узле, длины прилегающих к нему ребер и положение близлежащих узлов фронта. Если количество узлов фронта всего 3 (рис. 4, а), то добавляется элемент сетки, а сам фронт удаляется (блоки 6-7).
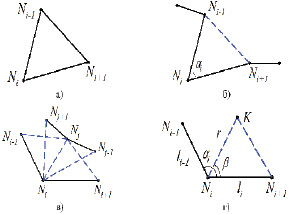
Рис. 4. Формирование элементов в зависимости от геометрии фронта
Следующей возможной ситуацией является срезание фронта (блоки 8-9), которое производится при условии
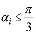
или же
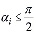 и
и 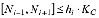 ,
,
где Kc=1,2 – коэффициент удлинения ребра при срезании (рис. 4,б). Необходимым условием, допускающим срезание фронта, также является отсутствие в треугольнике, образованном узлами N i-1, Ni , Ni+1, других узлов. В случае выполнения всех условий в триангуляцию добавляется элемент с узлами Ni-1, Ni , Ni+1, а узел Ni исключается из фронта.
Если срезание фронта невозможно, выполняется поиск ближайших узлов фронта, лежащих в секторе, образованном ребрами 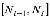 и
и 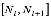 (блок 10). При существовании некоторого узла Nj, расстояние до которого
(блок 10). При существовании некоторого узла Nj, расстояние до которого 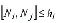 , среди четверки возможных элементов, включающих отрезок
, среди четверки возможных элементов, включающих отрезок 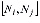 (показаны штриховыми линиями на рис. 4,в), выполняется поиск элемента с наилучшим качеством по критерию отношения самой короткой стороны треугольника к самой длинной. Если такой треугольник является корректным (не имеет пересечений с линиями фронта), производится добавление выбранного элемента в триангуляцию, а текущий фронт разделяется на два, которые в дальнейшем рассматриваются самостоятельно (блок 12).
(показаны штриховыми линиями на рис. 4,в), выполняется поиск элемента с наилучшим качеством по критерию отношения самой короткой стороны треугольника к самой длинной. Если такой треугольник является корректным (не имеет пересечений с линиями фронта), производится добавление выбранного элемента в триангуляцию, а текущий фронт разделяется на два, которые в дальнейшем рассматриваются самостоятельно (блок 12).
В случае, когда не произошло ни срезания, ни разделения фронта, внутрь области добавляется новый узел K (рис. 4, г), формируется элемент триангуляции с узлами, Ni, Ni+1, K, и узел K добавляется во фронт между Ni и Ni+1 (блок 13). При позиционировании узла используются следующие правила: угол 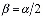 при
при 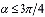 или
или 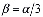 при
при 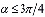 ; длина ребра
; длина ребра
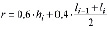 .
.
Значение длины ребра уменьшается, когда расстояние от нового узла до противолежащего участка фронта оказывается меньше 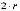 . В данной ситуации целесообразно использовать в качестве длины ребра половину этого расстояния.
. В данной ситуации целесообразно использовать в качестве длины ребра половину этого расстояния.
Если ни один из четырех рассматриваемых на рис. 4 вариантов построения (блоки 6-13) не привел к образованию новых элементов, то локальный шаг триангуляции уменьшается на 20 % (блок 15), производится возврат к блоку 10, и анализ ситуации повторяется.
После заполнения элементами области триангуляции, выражающегося в сокращении всех фронтов, производится оптимизация полученной сетки двумя способами:
- в случае вхождения узла сетки в 8 и более элементов производится локальное перестроение сетки путем разделении узла на 2, приводящее к уменьшению числа вхождений и увеличению минимальных значений углов в элементах (блок 17);
- итерационное сглаживание сетки путем переноса каждого внутреннего узла сетки в точку центра масс системы треугольников, содержащих данный узел (блок 18).
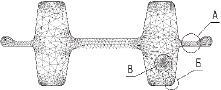
Результаты работы описанного алгоритма представлены на рис. 5. Так, на рис. 5,а показана сетка, построенная с изначально заданным количеством элементов 100, вследствие дробления границы при формировании исходного фронта и использования локального шага триангуляции реальное количество элементов увеличилось до 1772. На участке А можно наблюдать сгущение сетки, необходимое для моделирования затекания металла в облойную канавку. Сгущение на участке Б и аналогичных ему способствует моделированию движения элементов вдоль радиусов закругления штампа. На участке В сгущение элементов сформировано искусственно для демонстрации возможностей алгоритма. Сетка, приведенная на рис. 5, б, построена с заданным количеством элементов 1000, реальное количество составило 1843. Здесь также присутствуют сгущения в облое и на радиусах закругления.
Заключение
Применение описанного алгоритма для триангуляции типичных сечений поковок показало его способность формировать двумерные сетки из треугольных элементов, соответствующие всем поставленным выше требованиям. При решении задачи триангуляции первоначально трудно определить количество элементов, необходимое для качественного заполнения области. Предложенный подход позволяет полностью решить эту проблему для любой формы заготовки. Создаваемые на его основе сетки могут использоваться в двумерных задачах моделирования пластического формоизменения: в осесимметричном случае для круглых в плане поковок и плоском случае для удлиненных поковок, а также при дискретизации полигональных поверхностей в трехмерных задачах.
 а)
а)
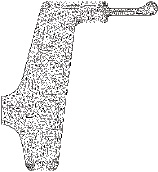 б)
б)
Рис. 5. Примеры триангуляции двумерных областей в задачах ОМД
Рецензенты:
Дементьев В.Б., д.т.н., профессор, директор Института механики Уральского отделения РАН, г. Ижевск;
Добровольский В.И., д.т.н., профессор, проф. каф. «Сопротивление материалов», ФГБОУ ВПО «Ижевский государственный технический университет имени М.Т. Калашникова», г. Ижевск.
Работа поступила в редакцию 04.06.2014.
Библиографическая ссылка
Покрас И.Б., Ахмедзянов Э.Р. АЛГОРИТМ ФОРМИРОВАНИЯ ДВУМЕРНОЙ СЕТКИ КОНЕЧНЫХ ЭЛЕМЕНТОВ В ЗАДАЧАХ МОДЕЛИРОВАНИЯ ПЛАСТИЧЕСКОГО ФОРМОИЗМЕНЕНИЯ // Фундаментальные исследования. 2014. № 9-1. С. 29-35;URL: https://fundamental-research.ru/ru/article/view?id=34636 (дата обращения: 14.02.2026).