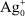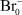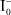Технологии контролируемого формирования наноразмерных структур с заданными свойствами являются одними из приоритетных направлений современной физики твердого тела и смежных с ней областей. Особый интерес в настоящее время представляет разработка методик поатомной сборки кластеров различных химических элементов или соединений на границах раздела двух и более фаз микронного масштаба в объеме различных композиционно-дисперсных материалов. Примером такой ситуации может являться полимерная композиция на основе ионообменной смолы с микровключениями из различных металлов, придающих данному материалу дополнительные электронопроводящие свойства [5], или стеклянная матрица с нанокомпозитным наполнителем из фоточувствительной системы AgI–Ag для создания гибридных «плазмон-экситонных» наноструктур [1]. Как правило, для получения таких и подобных им материалов преимущественно используются различные методы фотолитографии, основанные на диффузии атомов, стимулированной оптическим излучением и вариацией температуры [6, 9]. Однако применимость названных методов ограничена требованием к оптическим свойствам основного материала (матрицы) и содержащихся в нем микровключений. Например, первый должен обладать прозрачностью к ультрафиолетовому излучению, а включения, наоборот, сильно поглощать его. От перечисленных ограничений свободен электротопографический (ЭТГ) метод [4], основанный на эффекте коалесцентного формирования атомных структур по поверхности микрокристаллических включений, стимулированного внешним электрическим полем.
Впервые описанный эффект был обнаружен в 1970 году авторами [4] на примере фотоэмульсионных микрокристаллов (МК) галогенидов серебра (AgHal), распределенных в желатиновой матрице. Показана возможность направленного формирования атомных кластеров металла на поверхности МК в зависимости от напряженности электрического поля, времени его экспозиции и особенно электрофизических характеристик материала залегания – удельной электропроводности σG и диэлектрической проницаемости желатины εG, определяемых ее влагосодержанием PV, а также от толщины dp и диэлектрической проницаемости εp подложки, предотвращающей электрический пробой дисперсной системы [4]. Благодаря вариации столь значительного количества параметров возможно управление коалесценцией атомов в нужном направлении. Однако фактором, сдерживающим применимость ЭТГ-метода в нанотехнологиях, является отсутствие представлений о кинетических процессах названного эффекта. Поэтому в настоящей работе предлагается феноменологическая физико-математическая модель кинетики электрополевой коалесценции атомов серебра на примере дисперсно-распределенных в желатине МК AgBr сферической формы диаметром r = 10–6 m, содержащих варьируемую примесь ионов йода I– в диапазоне его концентраций 1–45 % от общей концентрации ионов брома Br– .
Физико-математическая модель. Для описания кинетических процессов составлялась система одномерных уравнений непрерывности, справедливых для МК AgHal названных размеров [2]. Модель учитывает атомы серебра Ag, группируемые полем не только на поверхности МК, но и в их глубине, а также концентрационную кинетику глубинных атомов галогенов – брома Br и йода I. Кроме перечисленных атомов в систему включены уравнения, отражающие кинетику концентраций катионов серебра Ag+, катионных вакансий VAg, анионов брома Br– и йода I– с их вакансиями VBr и VI, а также темновых электронов e и дырок h, совместно образующихся на стадии синтеза таких МК и находящихся в термодинамическом равновесии при рассматриваемой температуре T в диапазоне 278–303 K. В модели также учитывается характер распределения напряженности электрического поля на границе раздела МК и желатиновой матрицы в зависимости от ее
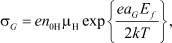
где aG – диаметр молекулы желатины, а μН и n0Н – соответственно подвижность и начальная концентрация протонов, образующихся в биополимере при диссоциации адсорбированных им молекул воды [4]; Ef – напряженность поля в фотоэмульсии.
Как правило, для формирования серебряных кластеров используются импульсные поля длительностью от 0,1 s и более [4]. Поэтому для моделирования был выбран часто встречающийся и технологически просто реализуемый видеоимпульс напряжения U колоколообразной формы, описываемый уравнением вида [2]
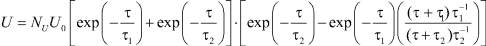 , (1)
, (1)
где NU = 10,49 – поправочный коэффициент; U0 – начальное напряжение импульса; τ = 0,2 s – его длительность, а τ1 = 2,5·10–2 s и τ2 = 4,5·10–2 s – длительности переднего и заднего фронтов видеоимпульса.
Согласно [3], при указанной величине τ существенно проявление релаксационных процессов поля как в объеме МК AgHal Ek, так и Ek на его поверхности ESk. Поэтому с учетом экспериментально исследованных систем МК AgBr – желатина (фотоэмульсий) толщиной df и диэлектрической проницаемостью εf [4], уравнения для Ek и ESk запишутся в виде [3]
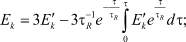 (2)
(2)
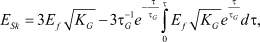 (3)
(3)
где 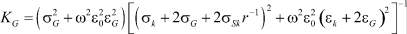 [7];
[7];
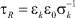 – время ионной релаксации МК AgHal;
– время ионной релаксации МК AgHal; 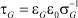 – время протонной релаксации желатины;
– время протонной релаксации желатины; 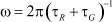 – циклическая частота;
– циклическая частота; 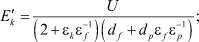
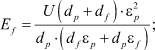
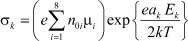 – удельная электропроводность МК и
– удельная электропроводность МК и 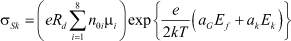
– его поверхностная электропроводность; 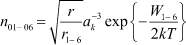 – начальные концентрации для ионов и ионных вакансий (причем, n05 = αn03);
– начальные концентрации для ионов и ионных вакансий (причем, n05 = αn03); 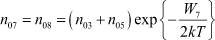 – для электронов и дырок;
– для электронов и дырок; 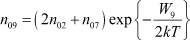 и
и 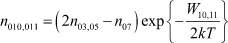 – для соответствующих атомов;
– для соответствующих атомов; 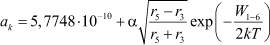 – постоянная кристаллической решетки AgBr; α – коэффициент, характеризующий долевое содержание примеси ионов йода в МК AgBr. Следует отметить, что в рассматриваемой модели диэлектрическая проницаемость МК AgBr εk является функцией от α и T, а εG – от последнего параметра и PV. В свою очередь, εf есть функция от εk, εG и объемной доли МК AgHal в желатине PAgHal. Математическая запись перечисленных зависимостей подробно рассмотрена в нашей обобщенной работе [8]. Вышеизложенное позволяет записать систему кинетических уравнений в общем виде для всех рассматриваемых частиц МК AgBr совместно с уравнением Пуассона и соответствующими граничными условиями:
– постоянная кристаллической решетки AgBr; α – коэффициент, характеризующий долевое содержание примеси ионов йода в МК AgBr. Следует отметить, что в рассматриваемой модели диэлектрическая проницаемость МК AgBr εk является функцией от α и T, а εG – от последнего параметра и PV. В свою очередь, εf есть функция от εk, εG и объемной доли МК AgHal в желатине PAgHal. Математическая запись перечисленных зависимостей подробно рассмотрена в нашей обобщенной работе [8]. Вышеизложенное позволяет записать систему кинетических уравнений в общем виде для всех рассматриваемых частиц МК AgBr совместно с уравнением Пуассона и соответствующими граничными условиями:
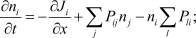 (4)
(4)
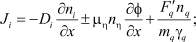 (5)
(5)
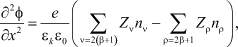
β = 0, 1, 2, 3; (6)
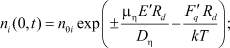 (7)
(7)
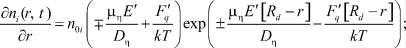 (8)
(8)
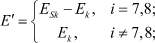
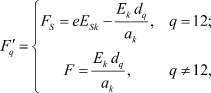 (9)
(9)
где ni – текущие концентрации частиц, участвующих в процессе коалесценции; Ji – потоки этих частиц; 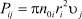 – вероятности захвата i-й частицей j-й частицы, причем для неподвижных ионов кристаллической решетки (i = 13–15) кинетические уравнения отсутствуют;
– вероятности захвата i-й частицей j-й частицы, причем для неподвижных ионов кристаллической решетки (i = 13–15) кинетические уравнения отсутствуют; 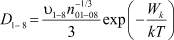 и
и 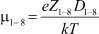 – диффузии и подвижности частиц массами m со скоростями их теплового движения
– диффузии и подвижности частиц массами m со скоростями их теплового движения 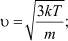
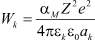 – потенциальная энергия взаимодействия ионов кристаллической решетки AgBr с ее постоянной Маделунга αM;
– потенциальная энергия взаимодействия ионов кристаллической решетки AgBr с ее постоянной Маделунга αM; 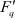 – силы, действующие на соответствующие атомы с их дипольными моментами dq и коэффициентами диффузии
– силы, действующие на соответствующие атомы с их дипольными моментами dq и коэффициентами диффузии 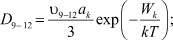
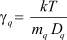 – коэффициент сопротивления среды; φ – потенциал, создаваемый всеми электрически заряженными частицами МК AgHal; Z = 1 – кратности их зарядов;
– коэффициент сопротивления среды; φ – потенциал, создаваемый всеми электрически заряженными частицами МК AgHal; Z = 1 – кратности их зарядов; 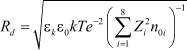 – дебаевский радиус; x и t – текущие координата и время. Расшифровка индексов параметров, входящих в (4)–(9), приведена в табл. 1, а в табл. 2 – название, физические и геометрические значения некоторых из них, а также физических постоянных, при которых проводилось численное решение системы. Отметим, что содержащиеся в уравнениях (4)–(9) слагаемые, индексы параметров которых отсутствуют в табл. 1 (прочерк), обращаются в нуль.
– дебаевский радиус; x и t – текущие координата и время. Расшифровка индексов параметров, входящих в (4)–(9), приведена в табл. 1, а в табл. 2 – название, физические и геометрические значения некоторых из них, а также физических постоянных, при которых проводилось численное решение системы. Отметим, что содержащиеся в уравнениях (4)–(9) слагаемые, индексы параметров которых отсутствуют в табл. 1 (прочерк), обращаются в нуль.
Как видно из системы уравнений, модель позволяет рассчитать, в частности, электрополевую коалесценцию глубинных (i = 9) и поверхностных (i = 12) атомов Ag в зависимости от очень многих физических параметров компонент, входящих в композиционный материал, а также от термодинамических факторов окружающей среды. С практической точки зрения интерес представляет оценка n9 и n12 при вариации следующих технологически просто реализуемых и контролируемо управляемых параметров: U0, T и α. Для рационального решения системы (4)–(9) с начальными и граничными условиями (7), (8) методом Рунге ‒ Кутта в ней было выполнено обезразмеривание уравнений. Расчет n9 и n12 проводился при F = FS (достигаемой вариацией PV) и объемной концентрации МК AgBr или AgBr(I) в фотоэмульсии 30 %. При этом поверхность МК представлялась сферическим слоем толщиной, равной Rd, и объемом
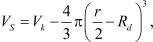
где 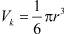 – объем всего МК. Результаты численного моделирования приведены на рис. 1 и 2, где ось ординат выражена в единицах безразмерной концентрации N атомов Ag.
– объем всего МК. Результаты численного моделирования приведены на рис. 1 и 2, где ось ординат выражена в единицах безразмерной концентрации N атомов Ag.
Таблица 1
Индексы параметров, входящих в уравнения (4)–(9)
|
Параметры |
i |
j |
l |
η |
q |
|
Ag+ |
1 |
– |
9–12, 14, 15 |
1 |
– |
|
VAg |
2 |
– |
9–11, 13 |
2 |
– |
|
Br– |
3 |
– |
9–11, 13 |
3 |
– |
|
VBr |
4 |
– |
9–11, 14, 15 |
4 |
– |
|
I– |
5 |
– |
9–11, 13 |
5 |
– |
|
VI |
6 |
– |
9–11, 14, 15 |
6 |
– |
|
e |
7 |
– |
9–13 |
7 |
– |
|
h |
8 |
– |
9–12, 14, 15 |
8 |
– |
|
Ag |
9 |
1–11 |
10, 11 |
– |
9 |
|
Br |
10 |
1–11 |
9, 10 |
— |
10 |
|
I |
11 |
1–11 |
9, 11 |
– |
11 |
|
Ags |
12 |
1, 7, 8, 12 |
– |
– |
12 |
|
|
13 |
– |
– |
– |
— |
|
|
14 |
– |
– |
– |
— |
|
|
15 |
– |
– |
– |
— |
Таблица 2
Значения физических и геометрических параметров, выбранных для численных расчетов (некоторые данные взяты из [2])
|
№ п/п |
Параметр, его обозначение и размерность |
Значение |
|
|
1 |
2 |
3 |
4 |
|
1 |
Постоянная Больцмана, J/K |
k |
1,380658∙10–23 |
|
2 |
Диэлектрическая постоянная, F/m |
ε0 |
8,8541878∙10–12 |
|
3 |
Элементарный электрический заряд, C |
e |
1,6021892∙10–19 |
|
4 |
Эффективная масса электрона, kg |
m7 |
2,642∙10–31 |
|
5 |
Эффективная масса дырки, kg |
m8 |
4,555∙10–30 |
|
6 |
Масса атома серебра, kg |
m 9,12 |
1,791∙10–25 |
|
7 |
Радиус атома серебра, m |
r 9,12 |
1,44∙10–10 |
|
8 |
Масса иона серебра, kg |
m1 |
1,777∙10–25 |
|
9 |
Радиус иона серебра и его вакансии, m |
r 1,2 |
1,13∙10–10 |
|
10 |
Масса ионной вакансии серебра, kg |
m2 |
2,0∙10–20 |
|
11 |
Масса атома брома, kg |
m10 |
1,317∙10–25 |
|
12 |
Радиус атома брома, m |
r10 |
1,14∙10–10 |
|
13 |
Масса иона брома, kg |
m3 |
1,331∙10–25 |
|
14 |
Радиус иона брома и его вакансии, m |
r 3,4 |
1,96∙10–10 |
|
15 |
Масса ионной вакансии брома, kg |
m4 |
1,5∙10–20 |
|
16 |
Масса атома йода, kg |
m11 |
2,107∙10–25 |
|
17 |
Радиус атома йода, m |
r11 |
1,33∙10–10 |
|
18 |
Масса иона йода, kg |
m5 |
2,121∙10–25 |
|
19 |
Радиус иона йода и его вакансии, m |
r 5,6 |
2,2∙10–10 |
|
20 |
Масса ионной вакансии йода, kg |
m6 |
2,387∙10–20 |
|
21 |
Дипольный момент атома серебра, C∙m |
d 9,12 |
4,61430∙10–29 |
|
22 |
Дипольный момент атома брома, C∙m |
d10 |
3,65299∙10–29 |
|
23 |
Дипольный момент атома йода, C∙m |
d11 |
4,26182∙10–29 |
|
24 |
Энергия образования ионов в кристалле AgBr, J |
W 1–6 |
1,698∙10–18–1,089∙10–19∙kT |
|
25 |
Энергия образования электронов и дырок в кристалле AgHal, J |
W 7,8 |
2,3314918∙10–19 |
|
26 |
Энергия образования атомов серебра, J |
W 9,12 |
1,128∙10–19 |
|
27 |
Энергия образования атомов брома , J |
W10 |
1,342∙10–19 |
|
28 |
Энергия образования атомов йода, J |
W11 |
1,29∙10–19 |
|
29 |
Постоянная Маделунга для AgBr |
αM |
1,7476 |
|
30 |
Диэлектрическая проницаемость полиэтилентерефталата |
εp |
3,23 |
|
31 |
Толщина полиэтилентерефталатной подложки, m |
dp |
1,65∙10–4 |
|
32 |
Толщина фотоэмульсионного слоя, m |
df |
5∙10–6 |
Результаты моделирования
Рис. 1, а отражает кинетику изменения концентраций глубинных и поверхностных атомов Ag под действием видеоимпульса напряжения. Математический «портрет» последнего (рассчитан по [1]) наложен на график вместе с кинетическими кривыми релаксации Ek и ESk, величины которых при условии F = FS близки между собой. По рисунку видно, что определяющее влияние на начальный процесс формирования атомарных кластеров Ag играет длительность переднего фронта импульса напряжения. Характерно, что при времени релаксации поля τ ≈ 0,08 s оно стабилизирует n9 и n12 на величине, превышающей их исходную концентрацию на 16,2 %. Этим подтверждается экспериментальный факт существенной зависимости коалесценции атомов Ag от напряжения, имеющей пороговый характер. Ее демонстрирует рис. 1, б. По нему видно, что для рассмотренных размеров сферических МК AgBr резкое накопление атомов Ag на их поверхности начинается при U0 ≈ 1,2 kV, что полностью соответствует результатам исследований электронографических фотопластинок светочувствительностью 45 ед. ГОСТ [4], содержащих МК, близкие к сферической форме. Рис. 1, б, также показывает величину напряжения (U0 ≈ 1,8 kV), при которой n9 и n12 достигают одинаковых значений (при постоянстве остальных рассматриваемых факторов).
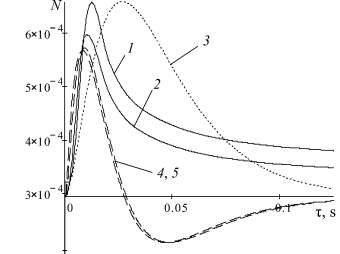 а
а
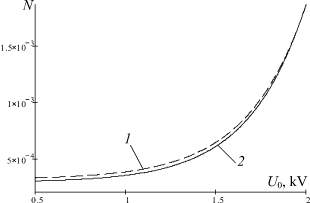 б
б
Рис. 1. Зависимость концентраций глубинных (1) и поверхностных (2) атомов Ag в МК AgBr: а – от формы импульса приложенного напряжения (3) и релаксации созданного им электрического поля в глубине (4) и на поверхности (5) МК (T = 298 K; U0 = 1 kV); б – от напряжения (T = 298 K)
 а
а
 б
б
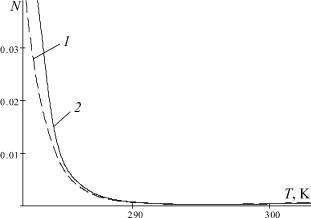
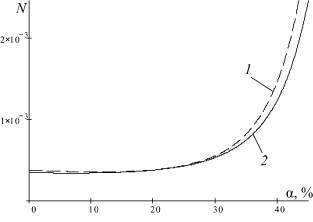
Рис. 2. Зависимость концентраций глубинных (1) и поверхностных (2) атомов Ag в МК AgBr: а – от температуры (U0 = 1 kV); б – от содержания примеси ионов йода (T = 298 K; U0 = 1 kV)
В свете сопоставления теоретически полученных зависимостей с экспериментальными представляет интерес оценка изменения n9 и n12 от T и α, что для ЭТГ-метода делается впервые. Результаты таких оценок приведены на рис. 2. Рис. 2, а, отражает названную зависимость от первого параметра, а рис. 2, б, – от второго (выражен в %). Из них видно, что изменения n9 и n12 от названных параметров носят экспоненциальный характер, идентичный установленной зависимости от напряжения. Результаты численного моделирования показывают, что электрополевая группировка атомов Ag в глубине и на поверхности беспримесного МК AgBr интенсивно происходит при понижении температуры, начиная с ее величины ~288 K, а при ее фиксированной величине 298 K, аналогичный рост n9 и n12 начинается при замещении в МК AgBr ионов Br– на ~27 % ионами I–. Таким образом, предложенная физико-математическая модель позволила не только подтвердить ранее установленные экспериментальные факты электрополевой коалесценции атомов Ag, но и предсказать возможность управления этим процессом вариацией температуры и концентрации вводимых ионов примесей (в нашем случае I–), что указывает на правомочность подходов и адекватность физических представлений о процессах в ЭТГ-технологии при построении модели.
Выводы
Обобщая результаты работы, сделаем из них следующие основные выводы:
- Разработана феноменологическая физико-математическая модель кинетики электрополевой коалесценции атомов Ag как в глубине, так и на их поверхности МК AgHal, распределенных в желатине, и учитывающая многие физические параметры компонент, входящих в дисперсную композицию (фотоэмульсию), а также термодинамические факторы окружающей ее среды.
- На примере распределенных в желатине МК AgBr и AgBr(I) сферической формы и размером 10–6 m показана возможность управления поатомной сборкой Ag не только за счет величины и формы прикладываемого напряжения, но и вариацией T и α в виде ионов I–.
Рецензенты:
Богатов Н.М., д.ф.-м.н., профессор, заведующий кафедрой физики и информационных систем Кубанского государственного университета, г. Краснодар;
Зарецкая М.В., д.ф.-м.н., профессор кафедры интеллектуальных информационных систем Кубанского государственного университета, г. Краснодар.
Работа поступила в редакцию 28.05.2014.
Окончание табл. 2
Библиографическая ссылка
Шишканов О.Н., Бойченко А.П. КИНЕТИЧЕСКАЯ МОДЕЛЬ КОАЛЕСЦЕНЦИИ АТОМОВ СЕРЕБРА В МИКРОКРИСТАЛЛАХ ЕГО ГАЛОГЕНИДОВ ПОД ДЕЙСТВИЕМ ЭЛЕКТРИЧЕСКОГО ПОЛЯ // Фундаментальные исследования. 2014. № 8-3. С. 607-613;URL: https://fundamental-research.ru/ru/article/view?id=34602 (дата обращения: 15.02.2026).