Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Гусев В.Б. 1 Кривошеев О.И. 1

---

1 Институт проблем управления им. В.А. Трапезникова Российской академии наук

В работе рассмотрена проблема анализа циклической динамики производственных и экономических систем с автономным управлением. Цель работы – изучить влияние механизмов автономного управления на характер динамики системы. Дана общая характеристика систем автономного управления. Предложены механизмы автономного управления производственными системами, аналогичные механизмам регулирования в технических системах. Рассмотрены модели экономических систем разной степени сложности с циклической динамикой. Проанализированы условия и примеры циклических режимов. В качестве основного инструмента автономного управления в этих моделях использовался механизм, управляющий инвестиционными потоками. Показано, что именно этот механизм является источником цикличности. Рассмотрены условия ацикличности таких систем. Приведены результаты анализа проблем, связанных с моделированием автономных саморазвивающихся систем. Показана связь между системными целевыми установками и характером циклической динамики саморазвивающихся систем.

Статья в формате PDF

687 KB

саморазвивающаяся система

автономное управление

моделирование

целеполагание

обратные связи

производственные циклы

1. Нейман Дж. Теория самовоспроизводящихся автоматов. – М.: Мир,1971.

2. Вишневский А.Г. Воспроизводство населения и общество: История, современность, взгляд в будущее. – М.: Финансы и статистика. 1982. – 287 с.

3. Разумовский С. М. Закономерности динамики биогеоценозов // Избр. труды. – М.: KMK Scientific Press, 1999.

4. Князева Е.Н., Курдюмов С.П. Законы эволюции и самоорганизации сложных систем. – М.: Наука, 1994. – 238 с.

5. Нейман Дж., Моргенштерн О. Теория игр и экономическое поведение. – М.: Наука, 1970.

6. Самуэльсон П. Экономика. Т. 1. – М.: МГП «АЛГОН» ВНИИСИ, 1992. – 333 с.

7. Егоров А.И. Основы теории управления. – М.: ФИЗМАТЛИТ, 2004. – 504 с.

8. Кривошеев О.И. Модель равновесного риска для инвестиционного бизнес-цикла // Вестник УГАТУ. – Т. 17, № 4 (57). – Уфа: УГАТУ, 2013. – С. 122–137.

Результаты функционирования большого количества саморазвивающихся систем [1], таких как социально-экономические и организационные [2], экологические и биологические [3], определяются качеством действующих механизмов управления. Эти механизмы по большей части носят автономный характер, что обусловлено особенностями их применения: ограниченным отрезком времени наблюдения, усеченным набором анализируемых параметров, упрощенным алгоритмом управления, ограниченными вычислительными затратами. Автономный характер управления в саморазвивающихся системах не всегда способен обеспечивать достижение целевой функции. Более того, автономное управление может само приводить к нестабильности – циклическим или даже хаотическим изменениям состояния системы.

Яркими примерами саморазвивающейся системы с автономным управлением являются национальная и мировая экономики, демонстрирующие циклический характер развития, непредсказуемые спады и кризисы. Тем не менее в условиях изменяющейся (возможно, дестабилизирующей поведение системы) внешней среды саморазвивающиеся системы обладают потенцией поддерживать в течение определенного времени установившийся режим функционирования. Последнее обеспечивается внутренними механизмами выбора как управляющих воздействий, так и критериев принятия решений в соответствии с состоянием самой системы и внешней среды [4].

По временным масштабам оказываемого эффекта механизмы автономного управления могут быть отнесены к краткосрочным или долгосрочным. Так, субъективные решения участников хозяйственной деятельности чаще носят краткосрочный характер [5], что может находиться в противоречии с долгосрочными интересами участников. В долгосрочном плане особое значение имеют механизмы, контролирующие показатели роста и устойчивости процесса развития.

Автономное управление направлено на достижение определенных целей в рамках располагаемых и довольно ограниченных возможностей и имеет следующие отличительные черты.

● Локальная вычислимость:

• Управление основано на локальной информации об объекте (как во времени, так и на множестве параметров).
• Управление соответствует внутренним целям системы.

● Модели автономного управления имитируют реальные механизмы принятия решений:

• Преимущества – не требуется полная информация об объекте управления и его окружении, не используются сложные вычислительные процедуры.
• Недостатки – возможны нежелательные эффекты, кризисы, циклы.

Автономное управление производственных систем

В качестве автономного управления производственных систем могут применяться известные в автоматическом управлении типы регуляторов [6]. Пропорциональная обратная связь функционирует при известном значении целевого показателя или заданном целевом критерии. С интегрирующим звеном – при наличии определенной доли потерь или рисков. С дифференцирующим звеном – при необходимости парирования быстрых возмущений. Объединяет эти типы обратной связи ПИД регулятор.

Модель производственного процесса с регулятором выпуска может быть представлена следующими уравнениями.

Объем выпуска –

y(t) = (z(t) – z₀)/a.

Затраты –

z(t) = z₀ + a·y(t – 1) + d·y(t – 1) + u(t).

Материалоемкость – a

Постоянные издержки – z₀.

Коэффициент потерь – d.

Управление –

u(t) = k·(ŷ – y(t – 1)) + l·i + m·D.

Плановый уровень – ŷ.

Интеграл невязки –

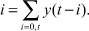
Дифференциал –

D = y(t) – y(t – 1).

Коэффициенты связи – k, l, m.

Эта модель ориентирована на достижение планового уровня выпуска ŷ с применением интегрирующего и дифференцирующего звеньев.

Режимы ПИД регулятора выпуска – ациклический и циклический (перерегулирование) представлены на рис. 1.

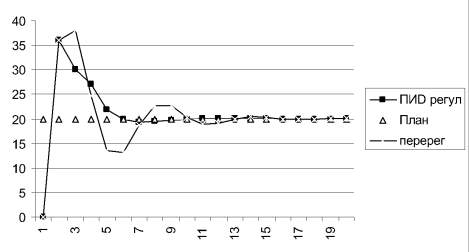
Рис. 1. Режимы ПИД регулятора выпуска

Экономические циклы

Другим примером автономного управления является модель макроэкономических циклов. Согласно Кейнсу, текущий объем валового национального продукта диктуется совокупным спросом на товары и услуги со стороны различных секторов экономики. Механизмы формирования спроса в секторах экономики различны, и это является причиной колебаний уровня и темпов изменения национального продукта. Если не учитывать чистый экспорт товаров и услуг, то основное уравнение выглядит следующим образом:

Y(t) = C(t) + I(t) + G(t).

Здесь Y(t) – валовой национальный продукт; С(t) – потребительские расходы населения; I(t) – планируемые инвестиции частных предприятий; G(t) – государственные закупки товаров и услуг. Модель Самуэльсона – Хикса [7] может быть представлена следующими разностными уравнениями

Y(t) = C(t) + I(t) + G(t);

C(t) = cY(t – 1) + b;

I(t) = v(Y(t – 1) – Y(t – 2));

G(t) = (1 + а)G(t – 1);

Y(t₀) = Y₀, G(t₀) = G₀ – начальные данные; c, b, v, а – параметры модели, где c = dC/dY – предельная склонность к потреблению.

Макродинамика модели Самуэльсона – Хикса представлена на рис. 2. Параметры модели: с = 0,2; b = 1; v = 2; а = 0,05. Полученный колебательный режим обусловлен рискованной инвестиционной политикой, при которой объемы инвестиций значительно превышают прирост ВНП.

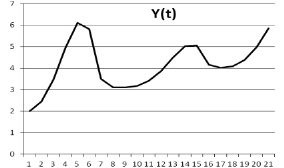
Рис. 2. Макродинамика модели Самуэльсона – Хикса

Автономное управление в модели Самуэльсона – Хикса может интерпретироваться следующим образом. Чистые инвестиции I(t) определяются изменением национального продукта в году t – 1. Подъем в экономике вызывает рост инвестиционных расходов. Стагнация же порождает спад чистых инвестиций. При ней нет стимула даже для поддержания имеющихся основных фондов. Валовых капитальных вложений не хватает на замену и ремонт изношенных зданий и сооружений.

Уравнения усложненной модели учитывают более детально процессы экономической деятельности: ценообразование, конечный спрос, фондообразование, инвестиции [8]. Эти уравнения имеют следующий вид:

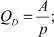
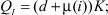
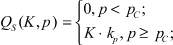
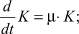
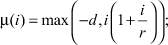
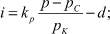
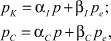
где p – цена; p_K – цена основных фондов; μ – скорость роста капитала, взаимно однозначно связанная со скоростью инвестиций, так называемое инвестиционное правило; Q_S – выпуск; Q_D – внешний спрос, определяется потребностями внешнего потребителя, например, если потребитель тратит фиксированную сумму A на производимый товар, то это гиперболическая зависимость; Q_I – внутренний инвестиционный спрос; i – внутренняя ставка процента Irr; d – скорость выбытия фондов; α_C, β_C – коэффициент текущих затрат собственного и внешнего продукта на единицу выпуска; kp – производительность единицы производственных фондов; α_I, β_I – коэффициент затрат собственного и внешнего продукта на единицу производственных фондов; K – производственный капитал; p_C – текущие затраты на единицу продукции; r – оценка риска.

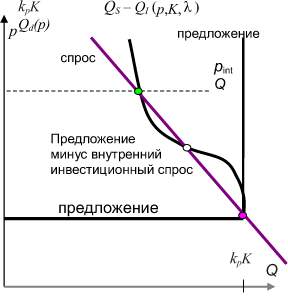
Модель системы рыночного равновесия обладает бистабильностью. На рис. 3 изображены кривые спроса, леонтьевская функция затрат/текущего предложения Q_S и Q_S – Q_I – предложение за вычетом инвестиций. При достаточно большом коэффициенте чувствительности к рентабельности k = r–1 при равновесном капитале K система всегда может иметь несколько равновесий.

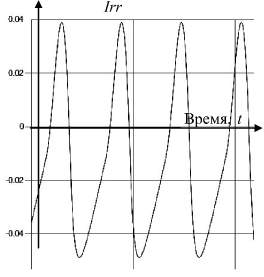а б

Рис. 3. а – бистабильная система рыночного равновесия: изображены кривые спроса (отрицательного наклона прямая), леонтьевская функция затрат/текущего предложения Q_S и Q_S – Q_I – предложение за вычетом инвестиций; б – колебания в зависимости от времени при r = 0,12

Источником цикличности в модели является бистабильность ценовых равновесий в коротком времени при малой величине r. При высоких ценах в верхнем равновесии рентабельность может быть положительна и тогда фонды возрастают – растяжение S-образной кривой внешнего предложения на рис. 3. Причиной S-образности является внутренний инвестиционный спрос, который растет с ростом IRR (рентабельности) и цен, тогда как предложение в состоянии насыщения. Это растяжение вправо приводит к исчезновению верхнего равновесия (динамическая бифуркация) с мгновенным переходом в нижнее. При низких ценах наблюдается падение фондов, что приводит к сжатию кривой внешнего предложения с исчезновением нижнего равновесия в некоторый момент.

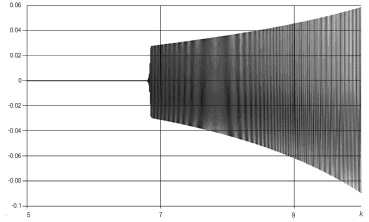
Рис. 4. Изменение амплитуды колебаний рентабельности при адиабатически медленном изменении параметра k = 1/r

Можно задаться вопросом, как подавить колебания посредством простейшего авторегулятора. Можно регулировать процентную ставку

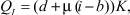
где .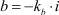

В зоне выше бифуркации (при k = 7,5) имеются автоколебания. В результате эксперимента по подавлению колебаний посредством политики управления процентной ставкой получено, что при kb ≈ 0,24 наблюдается бифуркация исчезновения цикла.

Амплитудная характеристика системы в зависимости от параметра k = 1/r приведена на рис. 4.

Заключение

Одной из центральных задач анализа механизмов автономного управления является определение условий их применимости в соответствии с предъявляемыми требованиями и критериями.

Автономное управление в саморазвивающихся системах может приводить к состояниям, не совпадающим с целевыми и не гарантирует устойчивого поведения системы. Построение механизмов обратной связи на основе целевых показателей в контуре управления, порождающих сходящийся итерационный процесс, является конструктивным приемом в управленческой практике.

Некоторые механизмы автономного управления выполняют функции локальных регуляторов. Область эффективности конкретного механизма автономного управления ограничена. Действие механизмов автономного управления может приводить как к колебательным процессам (перерегулирование), так и к непропорциональному развитию отдельных подсистем, вызывающему общий спад (несбалансированность).

В случае, когда поведение системы становится неудовлетворительным (нежелательные спады, осцилляции и т.д.), необходимо менять существующий алгоритм автономного управления, в том числе подключая механизмы внешнего управления. Такие подключения требуют дополнительных затрат ресурсов и могут носить временный характер.

Для того, чтобы система могла воспроизводить условия функционирования при определенном диапазоне изменения состояний внешней среды, механизмы автономного управления требуют соответствующей настройки. Исследование таких механизмов целесообразно осуществлять с помощью математических моделей процессов и систем, обладающих свойствами саморазвития.

Нижегородцев Р.М., д.э.н., зав. лабораторией, Институт проблем управления им. В.А. Трапезникова Российской академии наук, г. Москва;

Пащенко Ф.Ф., д.т.н., зав. лабораторией, Институт проблем управления им. В.А. Трапезникова Российской академии наук, г. Москва.

Работа поступила в редакцию 21.05.2014.

Библиографическая ссылка