Напряжения в слоях дорожной конструкции, вызывающие их деформации, в частности растрескивание, можно подразделить на две существенно различные группы:
- напряжения, вызванные внешними условиями, приложенными к поверхностям слоёв дорожной конструкции;
- напряжения, возникающие внутри дорожного полотна под влиянием неравномерного изменения элементов его объема вследствие каких-либо физических или химических процессов, например усыхания, охлаждения, диагенеза, рекристаллизации, с изменением объема, солнечной радиации, рельефа местности и условий проложения рабочих отметок.
Тогда как теория напряжений и деформаций первой группы достигла значительного развития и решены многие относящиеся к ним механические задачи, этого нельзя сказать о напряжениях и деформации второй группы. Относительно этих напряжений и деформаций поставлена только частная, так называемая температурная задача теории упругости, причем её решения, представляющие особенный интерес для проектировщиков и строителей, почти совершенно отсутствуют.
Неравномерные изменения связанных между собой элементов объема массива происходят вследствие изменения в массиве некоторой физической величины, например температуры, в некотором направлении или, другими словами, вследствие наличия градиента этой величины. Поэтому внутренние напряжения и деформации второй группы можно назвать вообще «объемно-градиентными» напряжениями и деформациями.
Для выяснения характера объемно-градиентных напряжений рассмотрим в качестве примера напряжения и деформацию элементарного твердого кубика ABCDFWHK, охлаждаемого сверху (рис. 1).
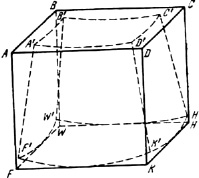
Рис. 1. Характер температурной деформации куба при охлаждении сверху
При равенстве температур во всех точках кубика температурных напряжений нет, и он сохраняет кубическую форму.
При охлаждении сверху верхний горизонтальный слой площадью ABCD стремится сократиться до размеров площади А1В1С1D1 но этому мешает связанный с ним лежащий ниже слой, температура которого выше, а площадь больше.
Вследствие взаимодействия этих слоев в них возникают напряжения: верхний слой растягивается нижним, а нижний сжимается верхним. То же можно сказать о любых двух соседних участках дороги – выемка и насыпь, за исключением поверхностного слоя, который растягивается особенно сильно.
Если отделить рассматриваемый кубик от массива, в нем произойдет деформация сдвига и изгиба. Каждый горизонтальный слой будет сдвигаться к своей центральной точке относительно лежащих ниже слоев. Поверхность ABCD станет вогнутой и займет положение А1В1С1D1, а поверхность FWHK – выпуклой и займет положение F1W1H1K1.
Таким образом, при охлаждении сверху каждый элемент охлаждающегося массива испытывает растягивающие, сжимающие, сдвигающие (касательные) и изгибающие напряжения. Но до наступления разрывов в однородном бесконечно протяженном массиве температурные напряжения проявляются как растяжения или сжатия, а деформации – как сокращения или расширения по вертикали [1].
При промерзании в начале зимы дисперсные грунты могут сначала несколько увеличивать свой объем вследствие увеличения объема при переходе воды в лед, но затем при дальнейшем охлаждении они уменьшают свой объем по причине обычного температурного сокращения твердых тел при охлаждении (рис. 2).
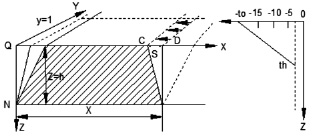
Рис. 2. Схема постановки задачи при приближенном расчете температурных напряжений в массиве, ограниченном горизонтальной и вертикальной поверхностями
Попытаемся приближенно определить напряжения, возникающие в верхнем слое дорожной конструкции при её дальнейшем охлаждении. С этой целью схематизируем задачу следующим образом.
Расположим систему прямоугольных координат (х, у, z), как показано на рис. 2, и будем рассматривать поперечник дороги как нижнюю четверть пространства, ограниченную плоскостями ху и yz, которые в данном случае являются свободными поверхностями.
Пусть при этом температуры в массиве дорожной призмы представлены кривой в правой части рис. 2. Тогда справа от плоскости yz в слое мощностью Δz = h все верхние элементы объема будут стремиться сократиться относительно нижних и ребро Оу отойдет вправо на расстояние ОВ; в то же время в массиве возникнут растягивающие напряжения, уравновешиваемые в пределах упругости силами сцепления.
Определим эти напряжения τ в сечении, параллельном плоскости yz, на расстоянии х от последней; при этом мы будем считать их касательными напряжениями, приложенными к поверхности массива. Такая замена объемных напряжений касательными физически оправдывается характером реальных температурных кривых (рис. 1), показывающим, что изменения температур и, следовательно, температурные напряжения сосредоточены преимущественно в поверхностном слое породы [2].
Задача эта статически неопределима, так как даны только равенство и противоположная направленность сил в любой точке выбранного сечения. Воспользуемся поэтому принципом совместности деформаций.
Рассечем массив плоскостью, параллельной плоскости yz, на расстоянии х от последней, тогда силы сцепления уже не будут уравновешивать силы растяжения; в отсеченной части напряженного слоя произойдет деформация сдвига, и отрезок BD, представляющий ширину отсеченной полосы, переместится влево на расстояние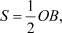 
в положение АС (рис. 2). Длину ОВ можно приближенно считать сокращением длины х при охлаждении на Δt = th – t0 градусов, то есть написать равенство
OB = 2s = αxΔt, (1)
где α – коэффициент линейного сокращения данного массива.
Если мы теперь восстановим действие сил сцепления, то последние произведут деформацию сдвига в обратном направлении, причем абсолютный сдвиг опять будет равен S.
Известно, что абсолютный сдвиг S связан со сдвигающей касательной силой Qx следующим соотношением:
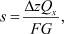(2)
где Δz – расстояние закрепленной плоскости тела от параллельной ей плоскости, по которой действует сила Qx; F – площадь, по которой действует сила Qx (в данном случае F = xy);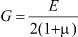 
– модуль упругости при сдвиге, где, в свою очередь, Е – модуль Юнга и μ – коэффициент Пуассона.
Приравнивая S из равенств (1) и (2), получим уравнение для определения силы Qx, действующей в направлении х:
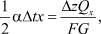(3)
откуда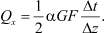 
(4)
Вводя вместо силы Qx тангенциальное напряжение τx = (Qx/F) и имея в виду, что (Δt/Δz) = grandzt, получим окончательно:
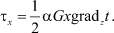(5)
При расчете градиента Δt/Δz за нормальную температуру ненапряженного грунта естественно, принимать среднюю температуру на глубине нулевых годовых амплитуд. Тогда слои при более высоких температурах будут относительно расширены и сжаты, а при более низких – относительно сокращены и растянуты.
Таким образом, тангенциальное напряжение τx в охлаждающейся дорожной конструкции, например в замёршем слое при наличии в нем свободной вертикальной поверхности yz, пропорционально градиенту температур по вертикали Δt/Δz, расстоянию х от свободной вертикальной поверхности, модулю упругости при сдвиге G и коэффициенту линейного расширения (сокращения) грунта α.
Приравнивая τx временному сопротивлению при сдвиге или разрывающему напряжению τb, из формулы (4) можно подсчитать расстояние х от свободной вертикальной поверхности, на котором касательные напряжения достигнут предельных значений, и произойдет разрыв (появится трещина).
Это расстояние равно
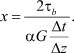(6)
Расчеты показывают, что расстояния между параллельными трещинами, получаемые по формуле (6), хорошо согласуются с наблюдаемыми в природе.
Из формулы (4) можно приближенно подсчитать и глубину зияющей трещины Δz в зависимости от ширины трещины с на поверхности и механических характеристик породы.
Действительно, принимая во внимание, что в формуле (1) OB ≈ xαΔt представляет собой ширину трещины на поверхности и что напряжения τx на линии растрескивания равны разрывающим напряжениям τb, по формуле (4) получаем:
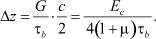(7)
Подход к приближенному расчету напряжений, возникающих в грунте вследствие его неравномерного высыхания, или, другими словами, вследствие образования градиента влажности, может быть совершенно аналогичным с постановкой вопроса в случае температурных напряжений. Характер напряжений в обоих случаях будет совершенно одинаковым, а различие заключается лишь в количественных характеристиках. Вместо коэффициента линейного сокращения (α) мы будем иметь коэффициент линейной усадки при усыхании (k), а вместо градиента температуры – соответственно градиент влажности (Δω/Δz), и формула для разрывающих напряжений τb при усыхании влажного глинистого грунта будет иметь вид:
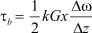. (8)
Появление морозобойных трещин на поверхности автомобильной дороги с асфальтобетонным покрытием является следствием промерзания влажного грунта земляного полотна и представляет собой сложный термодинамический процесс, протекающий в неоднородной капиллярно-пористой среде. Задача о протекании этого процесса является одной из наиболее сложных задач математической физики. Основной трудностью решения указанной задачи является необходимость учета изменения агрегатного состояния и теплофизических характеристик среды, в результате чего задача становится нелинейной. Кроме того, при промерзании и оттаивании одновременно с изменением температурного поля имеет место массоперенос, вызванный перемещением влаги.
Расчет такого единого процесса динамики температурного и влажностного полей при промерзании (оттаивании) крайне сложен. В значительном числе случаев, когда при промерзании отсутствует интенсивное морозное пучение, связанное с массопереносом, для практических целей можно ограничить расчет процесса промерзания влажного грунта расчетом его теплового режима с учетом фазовых переходов воды. Таким образом, в первом приближении расчет промерзания (оттаивания) грунта может быть значительно упрощен.
Для подобных задач существует значительное число методов расчета типового режима промерзающих (протаивающих) влажных грунтов без учета миграции в них влаги, но учитывающих фазовые превращения последней. В силу того, что в зависимости от физических свойств грунта фазовые переходы могут происходить практически полностью при температуре замерзания (грубодисперсные грунты), так и в спектре температур (тонкодисперсные), возможны две постановки задачи о промерзании без учета миграции.
Если влага замерзает при одной температуре, задача состоит в исследовании динамики температурных полей в мерзлой и немерзлой зонах при наличии подвижной границы раздела фаз между ними (задача Стефана). Скорость продвижения границы раздела фаз также подлежит определению. Если же замерзание (протаивание) влаги происходит в некотором диапазоне температур, т.е. с образованием зоны промерзания, задача еще более усложняется.
На основании вышесказанного и полученных зависимостей можно сделать следующие выводы:
- Существование свободной вертикальной поверхности предопределяет направление образующихся трещин, и в однородных массивах при этом условии должна формироваться система параллельных трещин на расстояниях х друг от друга (закон параллельности).
- Так как вектор градиента температуры перпендикулярен изотермическим поверхностям, а последние параллельны свободным горизонтальной и вертикальной поверхностям массива, то система полос, выделяемая системой параллельных трещин, должна разбиваться поперечными трещинами как система прямоугольников. Углы при сопряжении продольных и поперечных трещин должны быть прямыми (закон перпендикулярности).
- Разрывающие напряжения (τb) пропорциональны произведению линейного размера отдельности (х) на градиент температуры (Δt/Δz), поэтому при малых градиентах линейное сооружение распадается на крупные прямоугольные отдельности, а затем при увеличении градиентов эти отдельности последовательно делятся пополам трещинами последующих порядков генерации на все более мелкие отдельности.
- При сопряжении трещин в виде основания и перпендикуляра основание образуется ранее, более длинной трещиной, более низкого порядка генерации, а перпендикуляр – позже, более короткой трещиной, более высокого порядка генерации.
- В неоднородных породах с переменными в некоторых пределах морозобойные трещины могут быть извилистыми и не вполне параллельными друг другу, но перпендикулярность в точке сопряжений остается в силе.
- Кроме двух систем взаимно перпендикулярных вертикальных трещин, выделяющих прямоугольные призмы, последние должны разбиваться горизонтальными трещинами на параллелепипедальные отдельности.
- Анализ распределения полей влажности позволяет установить, что интенсивное изменение влажности грунта при промерзании происходит только непосредственно у фронта нулевых отметок.
Рецензенты:
Сушков С.И., д.т.н., профессор кафедры технологии и машин лесозаготовок, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Павлов А.И., д.т.н., профессор кафедры лесных, деревообрабатывающих машин и материаловедения, ФГБОУ ВПО «Ухтинский государственный технический университет», г. Ухта.
Работа поступила в редакцию 21.05.2014.
Библиографическая ссылка
Бургонутдинов А.М., Юшков Б.С., Бурмистрова О.Н. МЕТОДИКА ОБРАЗОВАНИЯ МОРОЗОБОЙНЫХ ТРЕЩИН НА АВТОМОБИЛЬНЫХ ДОРОГАХ И СПОСОБЫ БОРЬБЫ С ЭТИМ ЯВЛЕНИЕМ // Фундаментальные исследования. 2014. № 8-2. С. 285-289;URL: https://fundamental-research.ru/ru/article/view?id=34546 (дата обращения: 02.04.2025).