Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Петухова Я.В. 1

---

1 ФГБОУ ВПО «Вятский государственный гуманитарный университет»

В работе определяются и изучаются полутела обобщенных треугольных матриц. Полутелом называется алгебраическая структура с двумя бинарными операциями сложения и умножения, являющаяся группой по умножению и коммутативной полугруппой по сложению, причем умножение дистрибутивно относительно сложения с обеих сторон. Приведены основные понятия теории полутел, а также важнейшие примеры полутел обобщенных треугольных матриц. Более подробно рассмотрен частный случай матричных полутел – полутело верхних треугольных матриц n-го порядка с действительными коэффициентами. Сформулированы исходные свойства полутел обобщенных треугольных матриц. Представлен вид ядра матричного полутела, порожденного элементом 2. Получен критерий ограниченности полутела обобщенных треугольных матриц. Дана теорема о центре полутела обобщенных треугольных матриц. Как ее следствие получен критерий коммутативности полутела обобщенных треугольных матриц.

Статья в формате PDF

745 KB

полутело

конгруэнция

ядро

кольцо разностей

обобщенная треугольная матрица

полутело обобщенных матриц

1. Вечтомов Е.М., Черанева А.В. Полутела и их свойства // Фундаментальная и прикладная математика. – 2008. – Т. 14. – № 5. – С. 3–54.

2. Черанева А.В. Кольцо разностей полутела // Вестник Вятского государственного гуманитарного университета. Математика, информатика, язык. – 2007. – № 4. – С. 205–207.

3. Вечтомов Е.М., Петухова Я.В. Полутела обобщенных матриц // Современные проблемы математики и ее приложений: тезисы международной (45-я Всероссийская) молодежной школы-конференции (Екатеринбург, 2–8 февраля 2014 г.)

4. Вечтомов Е.М., Петухова Я.В. Полутела треугольных матриц // Алгебра и логика: теория и применение: тез. докл. междунар. конф. – Красноярск: Сибирский федеральный университет, 2010. – С. 17–18.

5. Кочкина М.А., Петухова Я.В. Конгруэнции полуполей нильмногочленов и полутел треугольных матриц // Международная молодёжная Интеллектуальная Ассамблея: сборник научно-исследовательских работ / отв. ред. М.В. Волкова – Чебоксары: НИИ педагогики и психологии, 2010. – С. 113–116.

Полутелом называется алгебраическая структура S с бинарными операциями сложения (+) и умножения (·) такая, что ⟨S, ·⟩ − группа, ⟨S, +⟩ − коммутативная полугруппа и умножение дистрибутивно относительно сложения с обеих сторон. Полутело с коммутативным умножением называется полуполем. Основные понятия теории полутел можно найти в [1].

Кольцом разностей полутела S называется пара ⟨R, f⟩, где R − кольцо и f : S → R − полукольцевой гомоморфизм, удовлетворяющий условию универсальности: для любого гомоморфизма g: S → T, где T − кольцо, существует единственный кольцевой гомоморфизм h: R → T, такой, что h ◦f = g. Любое полутело S имеет кольцо разностей, однозначно определенное с точностью до изоморфизма над S. Заметим, что кольцо R = {0} − нулевое в том и только в том случае, когда полутело S − зероидное, то есть a + b = a для некоторых a, b ∈ S [2].

Полутело с аддитивным сокращением a + c = b + c ⇒ a = b называется сократимым полутелом. Кольцом разностей сократимого полутела S является кольцо R(S), содержащее S в качестве подполукольца, для которого R(S) = S − S (здесь f − тождественное вложение S в R(S)).

Конгруэнцией на полутеле S называется любое отношение эквивалентности ρ на S, согласованное с операциями:

aρb, cρd ⇒ (a + c)ρ(b + d), (ac)ρ(bd) (∀a, b, c, d ∈ S).

Ядром полутела называется класс единицы 1 произвольной конгруэнции на нем. Нетривиальное полутело называется ограниченным, если оно как ядро порождается элементом 2 = 1 + 1.

Множество Con S всех ядер полутела S замкнуто относительно операций умножения и пересечения и образует полную модулярную алгебраическую решетку, которая изоморфна решетке всех конгруэнций полутела S по отношению включения.

Центром полутела S называется множество его элементов, коммутирующих с любым элементом из S. Легко видеть, что центр полутела S является подполутелом в S.

Пусть ⟨J, ≤⟩ – некоторое локально конечное упорядоченное множество, S – произвольное полутело и ⟨R, f⟩ – кольцо разностей для S.

Определим матричное полутело TJ(S) следующим образом. Множество TJ(S) состоит из всех таких обобщенных матриц A = (a_ij)J×J, что a_ij ∈ R для любых i ≠ j из J, a_ii ∈ S при i ∈ J и a_ij = 0, если неверно, что i ≤ j. [3]

Сложение матриц производится поэлементно. Для матриц (a_ij)J×J и (b_ij)J×J их произведение имеет вид (c_ij)J×J, где 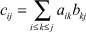при i ≤ j и c_ij = 0 в противном случае. При этом aiibik ∈ S для k = i и a_iib_ik = f(a_ii)b_ik ∈ R для k > i.

Теорема 1. ⟨TJ(S), +, ⋅⟩ – полутело, которое будет сократимым тогда и только тогда, когда S сократимо.

Примеры.

1. Если J = {1 < 2 < … < n} – n-элементная цепь, то T_J(R⁺) = V_n(R⁺) – полутело верхних треугольных матриц размерности n×n c действительными коэффициентами, все диагональные элементы которого положительны [4, 5].

Кольцо M_n(R⁺) всех верхних треугольных матриц n-го порядка с действительными элементами с обычными операциями сложения и умножения матриц является кольцом разностей сократимого полутела V_n(R⁺).

2. T_N(R⁺) – полутело бесконечных верхних треугольных матриц с действительными коэффициентами.

3. Если J – антицепь, то T_J(S) – полутело обобщенных диагональных матриц, изоморфное степени полутела S:T_J(S) ≅ S^J.

Рассмотрим основные свойства полутела верхних треугольных матриц.

Теорема 2. T_J(R⁺) = V_n(R⁺) – ограниченное полутело.

Доказательство. Рассмотрим элемент

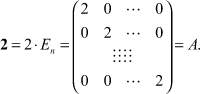
Покажем, что в главном ядре (2) содержится любой элемент из полутела V_n(R⁺), то есть любая верхняя треугольная матрица вида

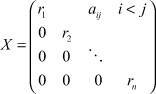
при r_i > 0. Существует такое натуральное m, что 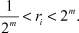Имеем A^m = 2^m ∈ (2) и A^–m = 2^m ∈ (2). Тогда

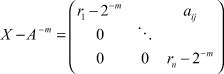
и

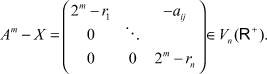
A^-m + (X - A^-m) = X и X + (A^m - X) = A^m. 

Значит, A^-m ≤ X ≤ A^m и, по свойству порядковой выпуклости ядер [1], любая матрица X  V_n(R⁺) включена в ядро (2). Получили, что V_n(R⁺) = (2) - ограниченное полутело. Теорема доказана.

На полуполе R⁺ существует ровно два ядра. Этими ядрами являются {1} и само R⁺. Действительно, рассмотрим произвольное ядро K в R⁺, K ≠ {1}. Пусть a ≠ 1, a > 1, a  K. Возьмем c  R⁺. $n  N такой, что a^-n < c < aⁿ, при этом a^-n, aⁿ  K. Тогда по свойству порядковой выпуклости ядер c  K. И поэтому R⁺ K и K = R⁺.

Значит, полуполе R⁺ имеет ровно два ядра: {1} и R⁺.Предложение 1. На полутеле верхних треугольных матриц второго порядка V₂(R⁺) существует ровно пять ядер.

Доказательство.

Имеем

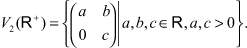
Его ядрами являются

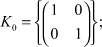
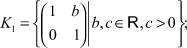
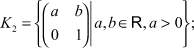
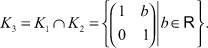
Пусть K произвольное ядро на полутеле V₂(R⁺). Покажем, что оно совпадает с одним из пяти указанных ядер.

Пусть 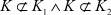. Докажем, что тогда K = V2(R+).

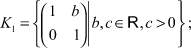
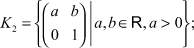
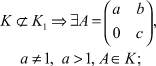
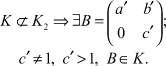
Существует l ∈ N a^l > 2.

Существует m ∈ N (c′)^m > 2.

Тогда

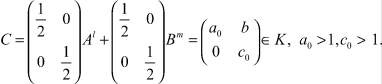
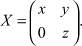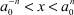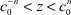Пусть Тогда найдется n ∈ N, для которого и . Поэтому C–n < X < Cn ⇒ X ∈ K, но Cⁿ – X ∈ V₂(R⁺) и X – C^–n ∈ V₂(R⁺). Поскольку C^–n, Cⁿ ∈ K, то по свойству порядковой выпуклости ядер X ∈ K. Значит, K = V₂(R⁺).

K ⊆ K₁.

Если

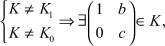
где c ≠ 1 или c = 1 ∧ b ≠ 0.

Если K ⊆ K₃, но K ≠ K₀ то K = K₃.

Покажем, что вместо b могут быть любые действительные числа. Пусть даны матрицы

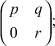
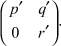
И пусть

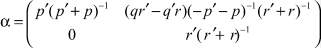
и

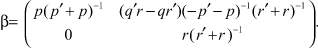
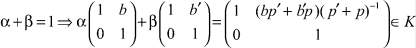
и

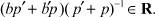
Если K ⊆ K₃ ∧ b = 0, то K = K₀.

Если K ≠ K₀, то K = K₁.

Пусть 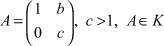. Покажем, что вместо с будет любое положительное действительное число. То есть ∀r ∈ R⁺, α + β = 1, то x < r < y и

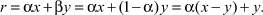
Существует

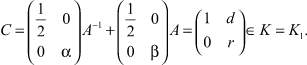
Значит, возводя A^–1 и A в степень, мы получим любые матрицы вида 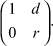То есть

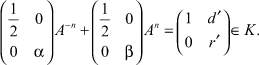
Случай K ⊆ K₂ вполне аналогичен случаю K ⊆ K₁. К найденным ранее четырем ядрам добавляется еще одно – K₂. Предложение доказано.

Для ограниченного полутела S существует естественная связь между его ядрами K и идеалами I кольца разностей M_n(R⁺):

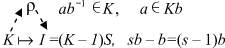
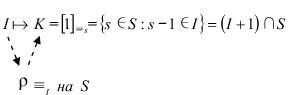
Обозначим через A_n множество пар (i, j) по всем натуральным числам 1  i  j  n. Множество A_n имеет (n²+n )/2 элементов. Каждому идеалу I кольца M_n(R⁺) сопоставляется вполне определенное подмножество A(I) в A_n, задающее общий вид матриц из I: если (i, j)  A(I), то элемент a_ij матриц из I может принимать любое числовое значение; если же (i, j)  A(I), то a_ij = 0 для всех матриц из I. Множество A(I) назовем конфигурацией идеала I. Например, A(M_n ⁺)) = A_n, конфигурацией нулевого идеала является пустое множество, а одноэлементное множество {(1, n)} служит конфигурацией наименьшего ненулевого идеала кольца M_n(R⁺).

Решетка идеалов кольца M_n(R⁺) изоморфна решетке конфигураций A(I). Решетка Con V_n(R⁺) изоморфна решетке конфигураций множества A_n.

Доказательство. Пусть n - натуральное число и M_n(R⁺) - кольцо всех верхних треугольных матриц n-го порядка с действительными элементами, рассматриваемое с обычными операциями сложения и умножения матриц. Тогда V_n(R⁺) есть множество всех матриц из M_{n с}положительными элементами на главной диагонали. Кольцо M_n(R⁺) = V_n(R⁺) - V_n(R⁺) является кольцом разностей полутела V_n(R⁺). Любой элемент из кольца M_n(R⁺) может быть представлен в виде разности элементов полутела V_n(R⁺). Элементы кольца разностей - любые действительные числа, которые могут быть получены из элементов полутела V_n(R⁺), путем вычитания.При n = 1 имеем M₁(R⁺) = R - это поле действительных чисел, а V₁(R⁺) = R⁺- полуполе положительных действительных чисел. При n ³ 2 полутело V_n(R⁺) неком- мутативно.Теорема 3. Для любого натурального числа n все ядра полутела V_n(R⁺) главные, решетка Con V_n(R⁺) дистрибутивна, имеет единственный атом и число ее элементов равно (n + 1)-му числу Каталана.Доказательство. Нам понадобятся так называемые числа Каталана [1]. Если n - неотрицательное целое число, то n-е число Каталана C_n находится как число сочетаний из 2n по n, деленное на n + 1: C_n= 2n(2n - 1)...(n + 2)/n!.

Для доказательства этого утверждения можно рассмотреть и подсчитать идеалы кольца M_n(R⁺), соответствующие ядрам полутела V_n(R⁺). Для первых значений n = 1, 2, 3, 4 утверждение проверено в [5]. Индукцией по порядку n матриц устанавливается, что кольцо M_n(R⁺) имеет ровно C_n+1 идеалов. Поле R = M₁ имеет 2 = C₂ идеала. Предполагаем, что утверждение доказано для всех натуральных чисел m < n. Далее, опираясь на индуктивное предположение, вид конфигураций и рекуррентную формулу С_n= С₀С_n-1+ С₁С_n-2+ ... + С_n-1С₀, подсчитывается общее число идеалов кольца M_n(R⁺) (n ≥ 2).

Заметим, что если полутело S имеет только конечное число ядер, то решетка Con S дистрибутивна [1]. На любом полутеле S следующее бинарное отношение: a  b  a = b или $с  S a + c = b, ‒ является отношением порядка, превращающим S в упорядоченное полутело.Предложение 3. В полутеле T_J(S) ядро, порожденное элементом 2, имеет вид

(2) = {(a_ij) ∈ T_J(S): ∃n ∈ N ∀i ∈ J 2^–n ≤ a_ii ≤ 2ⁿ}.

Теорема 4. Полутело T_J(S) является ограниченным тогда и только тогда, когда S ограничено и J конечно.

Теорема 5. Для любого сократимого полутела S центр матричного полутела T_J(S) совпадает с множеством диагональных матриц (a_ij) с равными элементами aii, принадлежащими центру полутела S.

Предложение 4. Полутело T_J(S) является полуполем тогда и только тогда, когда S – полуполе и J – антицепь.

Вечтомов Е.М., д.ф.-м.н., профессор, заведующий кафедрой алгебры и дискретной математики, ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров;

Чермных В.В., д.ф.-м.н., доцент, профессор кафедры алгебры и дискретной математики, ФГБОУ ВПО «Вятский государственный гуманитарный университет», г. Киров.

Работа поступила в редакцию 07.05.2014.

Библиографическая ссылка