Систематизированное расположение элементов в форме таблицы, придание каждому раз и навсегда определенного места позволило выявить удивительные закономерности в повторяемости свойств простых тел и их соединений. За полтора столетия, прошедших со времени предания гласности опыта периодической системы элементов, ничто не дало основания усомниться в справедливости одного из величайших установлений Природы. Классифицирующий признак «атомная масса» уступил место атомному номеру, но это позволило лишь четче подчеркнуть незыблемость Периодического закона (ПЗ). Создалась парадоксальная ситуация: характеристики объектов достаточно жестко фиксированы, но попытки найти общие математические закономерности количественного изменения свойств в зависимости от положения элемента или их совокупности в системе не имели особого успеха. Нам мало известно даже о тех принципах, которыми следует руководствоваться при формировании таких совокупностей.
В то же время тезис об определяющем влиянии порядкового номера, характеризующего количество носителей свойств в атоме, на численную величину самого свойства, с момента своего возникновения никогда не подвергался сомнению; более того, он заложен в формулировке Периодического закона. Поэтому существует необходимость детальнее проанализировать влияние числа (атомный номер, атомная масса) на энергетику атома (его свойства). При этом в качестве числа можно использовать характеристики общего плана, например, номер периода, семейства и т.д. На их фоне сам атомный номер является свойством, определенным на всем протяжении натурального ряда элементов. Это создает возможности для познания внутренней логики Периодического закона (ПЗ) в целом.
Свойства простых веществ, а также формы и свойства соединений элементов находятся в периодической зависимости от величины заряда их ядер. Но эта зависимость для конкретного члена не может быть периодической, т.к. заряд его ядра является характеристикой неизменной. Поэтому говорить о периодичности можно только применительно к некоторой совокупности, в которой элементы расположены в определенной последовательности и образуют упорядоченное множество – периодическую систему, свойства членов которой зависят от их порядковых номеров, и для элементов, находящихся на определенных интервалах друг от друга (периодах), характер изменения этих свойств повторяется.
Таким образом, Периодический закон – это наиболее общий закон строения упорядоченного химического множества. Поэтому пристальное внимание должно быть уделено форме представления такого химического множества, чье строение и является иллюстрацией ПЗ. Элементы могут быть по-разному упорядочены в пространстве, но любые варианты расположения должны иллюстрировать их принадлежность прежде всего к Системе.
Попытки вывести свойства химических элементов через величины зарядов ядер сталкиваются со значительными трудностями, что предсказывается принципом эмерджентности о несводимости свойств системы к простой сумме свойств слагаемых ее элементов. В то же время в различных отраслях естествознания развиваются представления о познании объектов через свойства систем, в которые указанные объекты входят как составные части.
Продуктивность познания свойств химических элементов зависит от ответа на вопрос: составными частями каких систем их следует рассматривать? Свойства химических соединений позволяют выявлять свойства входящих в них составляющих, но нет соединения, объединяющего в себе все химические элементы. Единственным множеством, в котором все они присутствуют одновременно в качестве равноправных членов, является периодическая система. В ней они действительно составные конструкционные детали, местоположение которых и определяет их функциональные свойства. То есть качества элементов дефинируются на основе сравнительного метода, реализуемого по определенным правилам согласно структуре Системы, выраженной в ее геометрической форме.
Из современных представлений о последовательности возникновения химических элементов во Вселенной вытекает, что Периодический закон – это закон развития, поскольку каждый вновь образуемый химический элемент обладал наперед заданными свойствами [2]. По закону Мозли заряды ядер все более тяжелых элементов возрастали монотонно, а свойства протон-нейтронных конструкций и структура электронной периферии атомов все время оказывались в соответствии с Периодическим законом. По сути, шло заполнение пустых ячеек в сконструированной самой Природой периодической Системе. Поэтому, принимая Периодический закон в качестве структурного закона системы элементов, его геометрию следует воспринимать не как абстракцию, а как меру приближения к познанию объективной реальности некоего явления, имеющего самостоятельную форму и содержание.
Чтобы человек смог нечто воспринимать, чтобы у него были разбужены чувства, нужен образ, идея феномена, а такую роль в химических науках и должна выполнять периодическая система.
Итак, если периодическая таблица – это система, классифицирующая элементы, то, в соответствии с принципами антиредукционизма, облик системы должен в общих чертах отражать облик классифицируемых элементов и данные о свойствах таковых должны выводиться из формы системы в результате строгого обоснования, заключающегося в самих принципах ее построения. Образно говоря, располагая знаниями об океане, мы можем на их основе совершенно точно предсказать свойства капли воды; обратный прогноз проблематичен – даже в самом общем и ограниченном виде.
Одномерный ряд химических элементов не позволяет продемонстрировать торжество Периодического закона, так как аналоги никак не выделяются в генеральном множестве. Разная емкость периодов приводит к тому, что они располагаются друг относительно друга на увеличивающихся в каждой паре периодов расстояниях. Стремление сгруппировать в пространстве химические аналоги привело к построению множества вариантов периодических систем. Аналоги в них, в отличие от одномерного исходного ряда, занимают совместно упорядоченное положение в пространстве. Каковы критерии предпочтительности тех или иных видов периодических систем?
Основное требование, предъявляемое к любому графическому варианту Периодического закона: он должен наглядно отображать общую картину повторяемости (по мере увеличения заряда ядер) характера трансформации свойств элементов. Результатом построений должна являться система, которая позволяет легко находить имеющиеся аналоги, прогнозировать новые, а также оценивать, сравнивать их свойства на количественно-качественной основе. То есть это должна быть классификационно-поисковая система.
Число графических вариантов ПЗ достигает, по разным оценкам, от одной до трех тысяч. Большинство представляет собою лишь геометрические образы, не подкрепленные какими-либо соображениями и содержащие нестыковки или произвольные допущения.
В отличие от них, естественные (натуральные) варианты, число которых не превышает десятков, основываются на тех или иных внятных принципах. Сошлемся на модификации, которые представляются наиболее удачными. Это таблицы Бейли, Бора - Томсена, Жанета, Клечковского, Сиборга [1–3] и т.п. Основные достоинства их в сравнении с прямоугольными формами:
- возможность неограниченного расширения элементов в раскрытое крыло сектора;
- возможность легко придать пирамидальной таблице «телесную» (Д.И. Менделеев) форму;
- возможность математизации Периодического закона;
- периоды в них не подвергаются сжатию или расширению, т.е. в таблице не возникает нелогичных пустот или сгущений.
Недостаток – стремление многих авторов выразить лестничный вариант в виде симметричной конструкции, что неизбежно влечет за собой необходимость соединять элементы-аналоги отрезками прямых, не имея для этого четких критериев. Предложено выравнивать лежащие на боку пирамиды по краевым элементам [5–7], что делает их архитектонику удобной для использования.
Выровняем таблицу Бора - Томсена по крайним элементам. Операцию осуществим двумя путями.
1. По благородным газам (рис. 1, элементы обозначены их порядковыми номерами). Электронные аналоги расположены один подле другого в горизонтальных строках, образуя компактно сгруппированные слои (снизу вверх) р-, d-, f-элементов, а пары начинающих периоды s-элементов помещаются на разных уровнях (их последовательность будем называть лучом), занимая по отношению к нижележащим горизонтальным слоям ступенчато-охватываюшее положение. Если рассматривать этот двухэлементный луч как облекающий, а слой из двух завершающих периоды как подстилающий (галоген – благородный газ), то они ограничивают своеобразный сектор, в котором располагаются все остальные химические элементы. Схождение луча и слоя в вершине сектора обуславливает то, что водород и гелий одновременно принадлежат как s-элементам, что соответствует их электронному строению, так и галогенам – благородным газам, что соответствует их химическим свойствам. Положение водорода и гелия оказывается инвариантным.
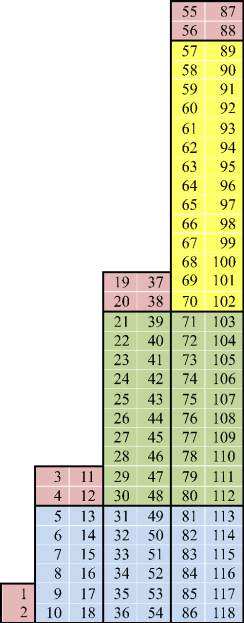
Рис. 1. Выравнивание таблицы Бора ‒ Томсена по благородным газам
Такая конструкция исключает пустые клетки в группах или периодах, дает возможность простого нахождения элементов-аналогов. Заполнение следующих после франциевого периодов требует лишь подстановки новых членов в раскрытое крыло сектора.
Подтверждается и натуральный характер рассматриваемой абстракции. Свернем плоскость таблицы так, чтобы состыковать концы предыдущих и начала следующих периодов. Получим структуру, имеющую множество аналогий в природе. Одни из наиболее распространенных – раковины улиток. Т.е. данный вариант это развертка пространственной формы, в основе которой лежит спираль.
При таком выравнивании члены натурального ряда сформированы в параллельные семейственные кланы. Лишь s-элементы пересекают их все, причем каждая пара аналогов имеет свой отклик в соответствующем семействе членов, близких по свойствам к элементам этой пары. Литий – натрий имеют отклик в виде Cu–Ag–Au; бериллию и магнию соответствуют Zn–Cd–Hg, кальций – стронций имеют продолжением Yb-No и т.п. При движении по семействам от р- к g-сходство вначале достаточно тесное (He–Ne–Ar–..., H–F–CI–... ), размывается, что связано с усложнением электронной структуры атомов. Но тем не менее оно существует. Это явление можно рассматривать в качестве инварианта, во многом подобного инвариантности, водорода – гелия: пары s-элементов (луч) входят составной частью в последовательности слоевых членов.
2. Выравнивание по s-элементам. Можно осуществить таковое, «подвесив» таблицу на щелочных металлах, или путем поворота ее вокруг последних на 180° опереть на них (рис. 2). Такая форма позволяет сосредоточить в слоях, параллельных s-элементам, неполные (в менделеевском смысле) аналоги из разных семейств. Но сами семейства, за исключением s-элементов, утрачивают свою обособленность, поскольку их составляющие «расползаются» по разным уровням. Это становится наглядным, если элементам каждого семейства придать свою окраску. Тем не менее у такой формы есть неоспоримое преимущество.
Поскольку порядковые номера элементов в ней растут слева направо (ось абсцисс) и снизу вверх (ось ординат), ее математическая анизотропия совпадает с таковой для I квадранта декартовой системы координат, и это снимает с конструкции налет виртуальности, который бы наблюдался в том случае, если бы порядок расположения номеров элементов был противоположный.
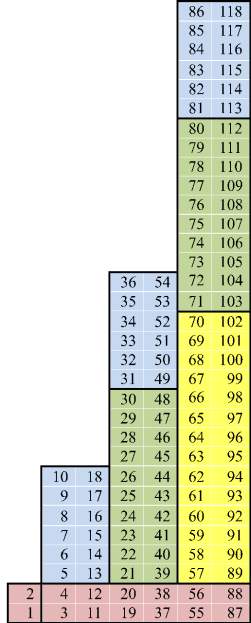
Рис. 2. Выравнивание таблицы Бора ‒ Томсена по s-элементам
Таким образом, выравнивание пирамидальных форм таблиц по краевым элементам приводит к четкому пространственному разграничению членов главных и побочных подгрупп (полных и неполных аналогов по Д.И. Менделееву), позволяет выявить множественность инвариантности положения ряда элементов в натуральной последовательности, что имеет важное значение для целей математизации закона, подчеркивает естественную природу полученных образов системы элементов, и, наконец, использование выровненных таблиц обеспечивает более реальное восприятие химической информации, которую они несут. Возможности таких таблиц мы рассмотрим в следующем сообщении.
Рецензенты:
Козик В.В., д.т.н., профессор, заведующий кафедрой неорганической химии, ФБГОУ ВПО «Национальный исследовательский Томский государственный университет», г. Томск;
Романенко С.В., д.х.н., профессор, заведующий кафедрой экологии и безопасности жизнедеятельности, ФГБОУ ВПО «Национальный исследовательский Томский политехнический университет», г. Томск.
Работа поступила в редакцию 30.04.2014.
Библиографическая ссылка
Спирин Э.К., Сытников А.М., Мальчик А.Г. НАТУРАЛЬНЫЕ ФОРМЫ СИСТЕМЫ ЭЛЕМЕНТОВ ДЛЯ ИЛЛЮСТРАЦИИ И МАТЕМАТИЗАЦИИ ПЕРИОДИЧЕСКОГО ЗАКОНА Д.И. МЕНДЕЛЕЕВА // Фундаментальные исследования. 2014. № 6-6. С. 1199-1203;URL: https://fundamental-research.ru/ru/article/view?id=34313 (дата обращения: 14.02.2026).



