Классическая технология анализа динамических режимов в электрических цепях заключается в составлении системы дифференциальных уравнений состояния, связывающих неизвестные токи и напряжения исследуемой цепи с заданными возмущающими функциями, и последующем ее интегрировании [5].
Ключевым этапом анализа является составление начальных условий, необходимых для определения постоянных интегрирования. Таковыми для цепи n-го порядка являются начальные значения искомых функций и их производных, включая (n – 1)-ю производную.
Начальные значения искомых функций определяются из уравнений состояния, рассматриваемых в момент времени t = 0 с учетом независимых начальных условий (токи в индуктивностях и напряжения на ёмкостях). Для отыскания начальных значений производных от искомых функций приходится многократно (n – 1 раз) дифференцировать исходную систему, каждый раз решая ее при t = 0. Входной информацией для решения систем уравнений являются результаты расчёта на предыдущем шаге [2].
Описанная процедура громоздка, трудоемка и часто носит далеко не очевидный характер. В этой связи актуальной задачей является поиск альтернативных способов решения, позволяющих упростить процедуру интегрирования системы дифференциальных уравнений состояния цепей высокого порядка и выработать легко формализуемый алгоритм.
Целью исследования является анализ канонической процедуры решения уравнений состояния с использованием схемной реализации алгоритма получения начальных условий в электрических цепях высоких порядков.
Материалы и методы исследования
Известно, что любая электрическая цепь описывается системой уравнений состояния, описывающих ее поведение в динамике и статике. Уравнения состояния вне зависимости от способа их получения (метод уравнений Кирхгофа, метод контурных токов, другие известные процедуры) составляют систему дифференциальных уравнений нескольких переменных, описывающих неизвестные реакции на заданные входные воздействия. Рассматриваемую систему уравнений методом исключения можно свести к одному дифференциальному уравнению, составленному относительно одной неизвестной (искомой) реакции электрической цепи [3].
Если исследуемая цепь линейна и инвариантна во времени, полное решение данного уравнения содержит принужденную (частное решение) и свободную (общее решение) составляющие. Свободная составляющая определяется в виде суммы экспонент 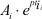 , число которых зависит от порядка цепи. В результате интегрирования дифференциальное уравнение преобразуется в систему n алгебраических уравнений, решаемую относительно постоянных интегрирования при заданных начальных (граничных) условиях Ai, определение которых является ключевым этапом анализа состояния цепи и сводится к решению уравнений состояния, составленных для момента t = 0+ с учетом независимых начальных условий, которым подчиняются напряжения на емкостях и токи в индуктивностях в соответствии с законами коммутации. Для отыскания начальных значений всех производных от искомой функции необходимо к системе уравнений состояния (n – 1) раз применить процедуру дифференцирования, решая при t = 0+. С увеличением порядка цепи число рассматриваемых уравнений растет, что в значительной степени усложняет процедуру решения [6].
, число которых зависит от порядка цепи. В результате интегрирования дифференциальное уравнение преобразуется в систему n алгебраических уравнений, решаемую относительно постоянных интегрирования при заданных начальных (граничных) условиях Ai, определение которых является ключевым этапом анализа состояния цепи и сводится к решению уравнений состояния, составленных для момента t = 0+ с учетом независимых начальных условий, которым подчиняются напряжения на емкостях и токи в индуктивностях в соответствии с законами коммутации. Для отыскания начальных значений всех производных от искомой функции необходимо к системе уравнений состояния (n – 1) раз применить процедуру дифференцирования, решая при t = 0+. С увеличением порядка цепи число рассматриваемых уравнений растет, что в значительной степени усложняет процедуру решения [6].
Предлагается схемная реализация процедуры определения зависимых начальных условий в электрической цепи, придающее этой операции наглядность и сводящееся к расчету резистивных цепей с источниками постоянных воздействий.
Для этого в анализируемой цепи выделяются все задающие воздействия – источники напряжения и тока и все независимые накопители энергии – индуктивности Lk и емкости Сk (рис. 1). Цепь имеет n независимых индуктивностей и n независимых ёмкостей. Порядок цепи равен 2n. Остальная часть цепи, условно изображенная в виде прямоугольника, чисто резистивная.
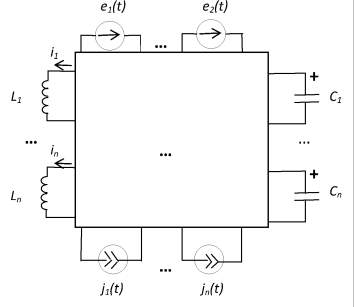
Рис. 1. Исследуемая цепь
Для определения начальных значений токов и напряжений составим расчётную схему для момента времени t = 0+ (рис. 2). Для этого заменим индуктивности источниками тока с задающими токами, равными iLk(0), а ёмкости - источниками напряжения с ЭДС, равными uCk(0), где iLk(0) и uCk(0) - токи в индуктивностях и напряжения на ёмкостях соответственно в момент времени t = 0+ определяются из расчёта докоммутационного режима в момент времени t = 0-.
Кроме исследуемых величин, в полученной резистивной цепи (рис. 2) необходимо найти напряжения uLk(0) на индуктивностях (источниках тока) и токи iCk(0) в ёмкостях (источниках напряжения) для отыскания производных 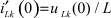 и
и 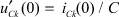 , являющихся начальными значениями для следующей схемы замещения.
, являющихся начальными значениями для следующей схемы замещения.
Значения первых производных искомых величин определяются из соответствующей схемы (рис. 3), эквивалентирующей первое дифференцирование уравнений состояния. Токи и напряжения в этой цепи фактически представляют первые производные этих величин.
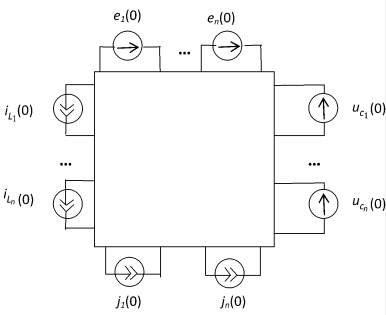
Рис. 2. Схема замещения для t = 0
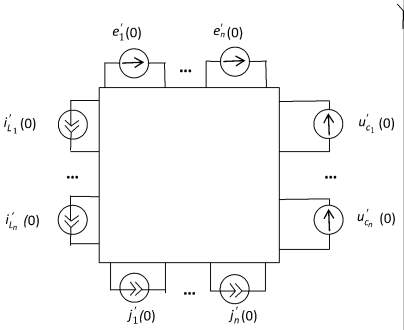
Рис. 3. Схема замещения для первых производных для t = 0
Как и в предыдущем случае, в полученной дискретной резистивной цепи для расчета начальных значений 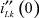 и
и 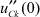 для следующей схемы замещения необходимо найти напряжения на индуктивностях (источниках тока) и токи в ёмкостях (источниках напряжения).
для следующей схемы замещения необходимо найти напряжения на индуктивностях (источниках тока) и токи в ёмкостях (источниках напряжения).
Далее процедура расчёта продолжается аналогично до получения начальных значений высших производных. Разумеется, если действующие в цепи источники питания развивают неизменные во времени воздействия, то во всех схемах, начиная со схемы (рис. 2) и далее, эти источники должны быть заменены короткозамкнутыми участками (источники напряжения) и разомкнутыми (источники тока).
Для источников с гармоническими воздействиями методика применима с поправкой на синусоидальные законы изменения входных сигналов, что обусловливает сохранение источников в схемах для производных.
Следует отметить, что при таком подходе конфигурации всех дискретных схем остаются неизменными и отличающимися только значениями воздействующих функций источников. Это позволяет воспользоваться любой из прикладных программ, например [4], для быстрой калькуляции искомых величин.
Заметим, что подобная технология может быть применена и при отыскании матриц связей для численного решения уравнений состояния [1].
Результаты исследования и их обсуждение
В качестве примера предлагаемая методика применяется для расчета цепи второго порядка (рис. 4).
В цепи даны параметры источников и потребителей:
e(t) = 200 sin(1000t + 90°)В; J = 10 A;
R1 = R2 = R3 = 10 Ом; L = 0,01 Гн; C = 100 мкФ.
Требуется найти начальные значения тока и их производных токов в ветвях.
Независимые начальные условия получим из расчёта докоммутационного режима (рис. 5).
До коммутации в цепи источник синусоидальной ЭДС был отключен, и существовали постоянные токи и напряжения. Поэтому сопротивление индуктивности L равно нулю (кз – замыкается накоротко), а сопротивление ёмкости С – бесконечности (хх – размыкается). Резистивные элементы и источник тока остаются без изменений.
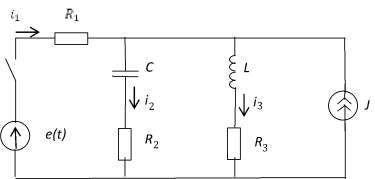
Рис. 4. Исследуемая цепь второго порядка
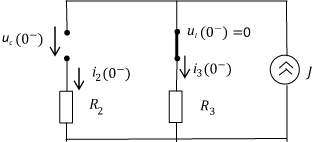
Рис. 5. Схема для t = 0 ̶
Законы (правила) коммутации запишутся:
i3 (0-) = i3(0+) = i3(0) = J = 10 A;
uC(0-) = uC(0+) = uC(0) = R3i3(0) = 100 B.
Схема для расчета начальных значений токов получена заменой реактивных элементов соответствующими источниками представлена на рис. 6.
По методу наложения определим начальное значение искомой величины:
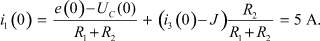
По первому закону Кирхгофа:
i2(0) = i1(0) + J - i3(0) = 5 A.
Составим схему замещения для отыскания начальных значений первых производных от токов.
Для этого определим начальные значения производных величин, подчиняющихся независимым начальным условиям, по формулам
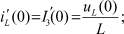
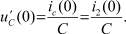
Из второго закона Кирхгофа для контура, содержащего ветви 2 и 3, определим напряжение на индуктивности (замененной на источник тока):
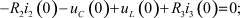
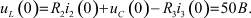
Получим начальные значения для схемы для производных
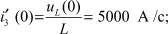
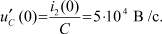
Схема замещения для отыскания начальных значений первых производных от токов изображена на рис. 7.
По методу наложения:
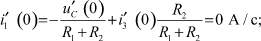
по первому закону Кирхгофа:
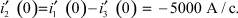
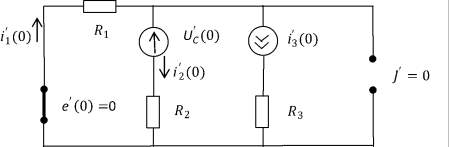
Выводы
Предлагаемая технология отличается высокой наглядностью, сводится к привычному расчету дискретных резистивных цепей с источниками постоянных воздействий.
Описанный способ определения начальных значений выходных сигналов и их производных любых порядков, связанный со схемной реализацией, легко формализуется и может быть частично автоматизирован, что делает его более привлекательным в сравнении с традиционным.
Рассмотренные резистивные схемы замещения могут быть применены при анализе динамических режимов в линейных электрических цепях численными методами (например, в пространстве состояний), преимуществом которых является полная автоматизация, что определяет практическую ценность представленной методики.
Рецензенты:
Труфанова Н.М., д.т.н., профессор, зав. кафедрой конструирования и технологий в электротехнике, ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь;
Кавалеров Б.В., д.т.н., доцент, зав. кафедрой «Электротехника и электромеханика», ФГБОУ ВПО «Пермский национальный исследовательский политехнический университет», г. Пермь.
Работа поступила в редакцию 30.04.2014.
Библиографическая ссылка
Рябуха А.А., Кузнецова Т.А. КАНОНИЧЕСКОЕ РЕШЕНИЕ УРАВНЕНИЙ СОСТОЯНИЯ ВЫСОКОПОРЯДКОВЫХ ЭЛЕКТРОДИНАМИЧЕСКИХ СИСТЕМ C ИСПОЛЬЗОВАНИЕМ ДИСКРЕТНЫХ РЕЗИСТИВНЫХ ЦЕПЕЙ // Фундаментальные исследования. 2014. № 6-6. С. 1154-1158;URL: https://fundamental-research.ru/ru/article/view?id=34304 (дата обращения: 17.12.2025).



