Современные методы проектирования породоразрушающего инструмента находятся на высоком уровне, но для получения максимального КПД от долота при бурении нефтяных и газовых скважин необходимо учитывать множество факторов [1]. Одним из этих факторов являются гидродинамические параметры потока промывочной жидкости в процессе бурения. Так как проводить анализ процессов, происходящих при бурении скважины, довольно сложно из-за большой глубины, то решением данной задачи может быть моделирование физических процессов бурения методом конечных элементов. В настоящее время инженерами по всему миру используется множество инструментов для проведения CFD расчётов, однако международный многолетний опыт использования программ данного типа говорит о преимуществе программного комплекса ANSYS Fluent для конкретной задачи. Важным в данном исследовании является то, что в программном комплексе ANSYS Fluent есть возможность моделирования двухфазных и многокомпонентных сред, в том числе дискретных гранулированных частиц, образующихся в результате разрушения породы. Для выполнения расчётов данного типа необходимы большие вычислительные мощности, однако использование средних параметров среды позволяет определить оптимальное соотношение между точностью получения результатов и временем, затраченным на расчёт. Такой подход позволит создать методику расчётов конструкций буровых долот на стадии проектирования породоразрушающего инструмента, а также системы промывки буровых долот, что значительно повысит основные показатели бурения, такие как механическая скорость и величина проходки на долото.
Постановка задачи
В данной задаче моделируется истечение промывочной жидкости из сопла долота в забой с размытием породы. В качестве промывочной жидкости для начала исследования были использованы параметры воды. Решение такой задачи основывается на численном решении уравнения Навье ‒ Стокса, реализованного в ANSYS Fluent, а момент перехода от ламинарного режима к турбулентному определяется критерием Рейнольдса [2], определяющим соотношение вязких и инерционных сил в потоке,
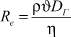 ,
,
где ρ – плотность среды; DГ – гидравлический диаметр; ϑ – скорость потока жидкости; η – динамическая вязкость среды.
Для моделирования гидродинамики течения использовалась двухфазная модель, где одна фаза представляет собой дискретные гранулированные частицы горной породы, другая фаза – промывочная жидкость. Для описания изменения свойств породы использовались эмпирические данные, полученные в работах [5–8].
Изменение вязкости гранулированных частиц описывается уравнением Gidaspow [6]:
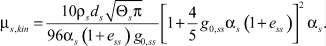
Объёмная вязкость сыпучих веществ определяет сопротивление при расширении и сжатии. Её можно выразить соотношением [7]:
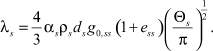
В плотных потоках при низкой скорости сдвига, где высокий предел концентрации твёрдых частиц, возникают напряжения в основном за счёт трения между частицами. Вязкость твёрдых частиц вычисляться по умолчанию не может, поэтому при определении вязкостного трения используется уравнение [8]:
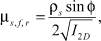
где ps – давление твёрдых частиц; φ – угол внутреннего трения, а I2D – второй инвариант девиатора тензора напряжений.
В потоках с высокой объёмной долей твёрдого вещества мгновенное столкновение является менее важным. Применение кинетической теории для таких потоков больше не является необходимостью, так как частицы находятся в контакте и в результате трения напряжения должны быть приняты во внимание.
В данной части исследование началось с расчёта мягких пород, 1–2 по коду IADC, что соответствует очень мягким и мягким породам с углом внутреннего трения 14–23°.
Численное моделирование и результаты расчётов
Для выполнения CFD расчёта была построена сеточная модель (рис. 1, а), состоящая из тетраэдрической и гексаэдрической сеток на двух доменах, соединённых проницаемым интерфейсом. Размерность сетки 7,5 млн элементов с максимальной скошенностью 0,84. Так же был создан призматический пограничный слой толщиной 1 мм (рис. 1, б).
 а
а
 б
б
Рис. 1. Сеточная модель: а – всей расчётной области; б – канала и пограничного слоя
Задача решалась в нестационарной постановке, с использованием модели турбулентности k–ε. Было получено, что при расходе в 1 кг/с промывочной жидкости через затопленную цилиндрическую насадку диаметром 20 мм через 1 секунду течение выходит на установившийся режим (рис. 2).
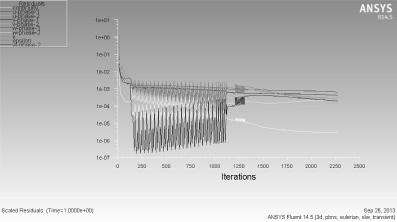
Рис. 2. График сходимости решения задачи
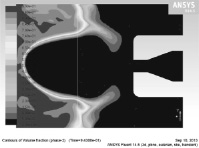
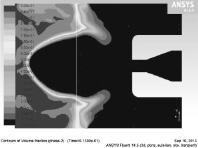
В результате получены картины распределения параметров по сечениям модели, которые позволяют получить необходимые для верификации данные (рис. 3–4). На рис. 3 а, б, в, г показано изменение объёмной доли породы со временем.
 а
а
 б
б
 в
в
 г
г
Рис. 3. Распределение объёмной доли твёрдой породы в разные промежутки времени: а – время расчёта 0,005 с; б – время расчёта 0,26 с; в – время расчёта 0,613 с; г – время расчёта 0,943 с
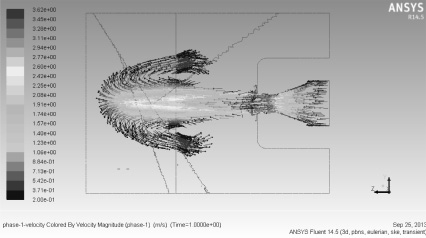
Рис. 4. Вектора скоростей истечения промывочной жидкости
Заключение
По результатам расчёта видно, что в данной постановке задачи для мягких и очень мягких пород глубина проникновения промывочной жидкости в породу составила порядка четырёх диаметров отверстия насадка, что говорит о приближенности численного моделирования к реальности [1]. Но для продолжения исследования необходимо проведение верификации модели и расчёт для других типов пород. А также учёт напряженно-деформированного состояния забоя и неравномерность свойств породы вследствие этого. Данная методика расчёта также позволяет оценивать вынос шлама, образовавшегося в результате воздействия струи промывочной жидкости на забой, его количество и зоны максимальной концентрации в затрубном пространстве, что косвенно может говорить о возможном сальникообразовании.
Рецензенты:
Штеренберг А.М., д.ф.-м.н., профессор, зав. кафедрой «Общая физика и физика неф тегазового производства» Самарского государственного технического университета, г. Самара;
Волокитин А.И., д.ф.-м.н., профессор кафедры «Общая физика и физика нефтегазового производства» Самарского государственного технического университета, г. Самара.
Работа поступила в редакцию 11.04.2014.
Библиографическая ссылка
Тютяев А.В., Сморкалов Д.В. РАСЧЁТ ИСТЕЧЕНИЯ ПРОМЫВОЧНОЙ ЖИДКОСТИ ИЗ НАСАДКИ БУРОВОГО ДОЛОТА В ANSYS FLUENT // Фундаментальные исследования. 2014. № 6-3. С. 495-498;URL: https://fundamental-research.ru/ru/article/view?id=34187 (дата обращения: 05.02.2026).



