Подробный обзор литературы, посвященной исследованию фильтрационных процессов, показывает, что в современных технологиях и методах воздействия на залежах с трудноизвлекаемыми запасами не найдено должного обоснования теории и практики фильтрации флюидов с учетом изменения структуры низкопродуктивного коллектора. Кроме этого, требует дальнейшего развития теоретическое положение по нестационарной пространственной фильтрации флюидов в деформируемой низкопродуктивной пористо-трещиноватой среде с учетом резкой колебательности коэффициентов проницаемости, гидропроводности и энергии в многослойных пластах, оказывающие наиболее существенное влияние на процесс выработки трудноизвлекаемых запасов. Как показывает практика эксплуатации многопластовых месторождений, увеличение добычи нефти путем совершенствования технологии выработки запасов из низкопродуктивных пластов равносильно открытию новых месторождений углеводородов.
Постановка задачи
Горное давление на пласт компенсируется как напряжениями твердого скелета массива, так и давлением жидкости. Изменение последнего возмущает напряженно-деформированное состояние пласта (НДС), т.е. изменение порогового давления в одной точке вызывает перестройку НДС всей системы и в том числе деформацию во всем пласте.
При изучении напряженно-деформируемого состояния пласта предполагается, что под действием приложенных внешних сил деформация пласта протекает без нарушения его сплошности [1]. Поэтому необходимо наложить ограничения на величину компонента деформации.
Рассмотрим упругое статическое состояние горизонтальной скважины, продольная ось которой составляет произвольный угол с линией простирания плоскости изотропии породного массива (рис. 1).
Введем прямоугольную декартову систему координат Оxyz таким образом, что ось Оz направлена вертикально вверх, горизонтальные оси Оx и Оy совпадают с линиями соответственно вкрест и вдоль простирания плоскости изотропии.
Упругое состояние трансверсально-изотропного массива описывается уравнением обобщенного закона Гука в системе координат Ox΄y΄z΄, полученной путем поворота Оxyz на угол φ вокруг вертикальной оси Oz, и имеет вид [2]
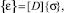
где
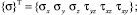
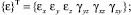
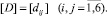
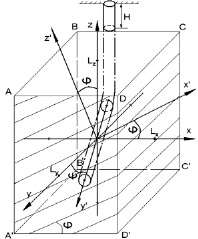
Рис. 1. Расчетная схема наклонного трансверсально-изотропного массива с горизонтальной скважиной
Здесь коэффициенты деформации dij определяются из [3].
Компоненты деформации также можно определить через перемещение u, v и w (по оси Ox, Oy и Oz соответственно) с помощью cоотношения Коши.
Граничные условия зададим в виде
u = v = 0, при
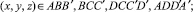
u = v = w = 0 при 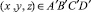 .
.
Далее нестационарная фильтрация жидкости к горизонтальной скважине в трансверсально-изотропной пористой среде (рис.1) описывается следующим уравнением, определяющим давление при пространственной фильтрации:
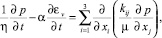
с граничными условиями
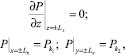
где 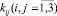 – коэффициенты проницаемости анизотропного (трансверсально-изотропного) пласта.
– коэффициенты проницаемости анизотропного (трансверсально-изотропного) пласта.
При этом полное напряжение [4] трансверсально-изотропного пласта может быть выражено через эффективное напряжение и давление в виде
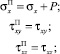
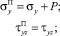
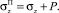
Характерной особенностью модели является предположение о том, что пористая матрица деформируется совершенно свободно до некоторого жесткого предела ε0.
Конечно-элементная модель
Рассмотрим трехмерный изопараметрический шестигранный конечный элемент первого порядка [1], для которого интерполяционный полином является линейной функцией локальных координат ξ, η, ζ (рис. 2). Пределы изменения локальных координат для всех элементов составляют 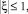
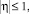
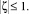 Функции формы такого элемента даются соотношениями вида
Функции формы такого элемента даются соотношениями вида
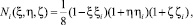
где ξi, ηi, ζi – локальные координаты узловой точки с номером 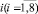 .
.
Интерполяционные соотношения для перемещений в трехмерном изопараметрическом элементе имеют вид
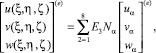
где uα, vα, wα – компоненты вектора перемещений в узлах «e»-го элемента.
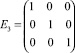 – единичная матрица.
– единичная матрица.
Интерполяционные соотношения для конечного элемента определяются как
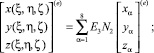
здесь xα, yα, zα – глобальные координаты узловой точки с номером α.
Эти соотношения можно представить в виде
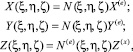
где N(e) – матрица функции форм элемента; X(e), Y(e), Z(e) – векторы узловых значений глобальных координат.
Матрица жесткости конечного изопараметрического элемента имеет вид:
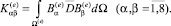
Здесь матрица градиентов 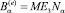 определяется из функции формы Nα.
определяется из функции формы Nα.
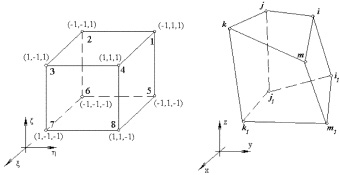
Рис. 2. Трехмерный изопараметрический элемент
В итоге матрицу жесткости изопараметрического элемента получим из
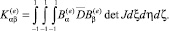 ,
,
численное интегрирование которого осуществляется методом Гаусса, т.е.
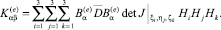
Здесь ξi, ηj, ζk – точки интергрирования Гаусса; n – порядок интегрирования; Hi, Hj, Hk – весовые коэффициенты.
Перемещение точек элемента определяем u(e) = N(e)U. Матрица конечной деформации имеет вид ε(e) = B(e)u(e), в свою очередь компоненты напряжений вычисляются из σ(e) = Dε(e).
Искомые значения определяются из решения систем линейных алгебраических уравнений [5]
KU = F,
здесь
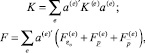
где 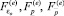 – векторы узловых сил конечного элемента статически эквивалентны действию конечной деформации,
– векторы узловых сил конечного элемента статически эквивалентны действию конечной деформации, 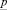 поверхностных и
поверхностных и 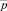 объемных сил.
объемных сил.
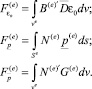
Рассмотренную выше матрицу жесткости элемента можно записать в виде
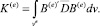
Аналогичным путем применяем процедуру для шестигранного изопараметрического элемента (рис. 2) к решению задачи фильтрации.
Вычислительный эксперимент
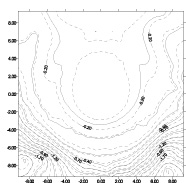
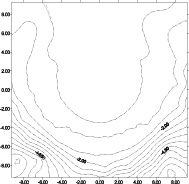
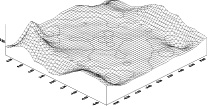
Деформируемое состояние наклонного под углом φ трансверсально-изотропного массива приводится с применением закона Гука и коэффициентов деформации. Численный эксперимент проводился по следующим данным: в качестве пород наклонных слоем взяты [2], аргиллит, алевролит, песчаник, известняк, модуль упругости которых имеет соответственно значения E = 1,34; 0,62; 2,95; 5(10-5 кг/см2) постоянного Пуассона соответственно υ(k) = 0,3; 0,2; 0,35; 0,11. Для трансверсально-изотропных слоев округленные упругие характеристики определяются E1 = 1,54·10-5 кг/см2; E2 = 0,98·10-5 кг/см2; модуль сдвига G2 = 0,36·10-5 кг/см2; υ1 = 0,22; υ1 = 0,25. При этом граничные условия учитываются при определении напряжений в наклонном под ψ = 30° пласте по X и Z. Сравнительные изолинии показаны на рис. 3 в случаях φ = 30° (пунктирные линии) и φ = 60° (сплошные линий). Общий вид функции деформации представлен на рис. 4.
Проведены различные варианты вычисления в зависимости от углов наклона плоскости изотропии и горизонтальной скважины φ, ψ.
Анализ результатов, приведенных в наклонном трансверсально-изотропном пласте, показывает, что с увеличением количества конечных элементов в дискретной модели тела наблюдается совпадение двух значащих цифр в значениях компонента перемещения u, нормальных напряжений σ, а также в значениях интенсивности напряжений и деформаций.
 а
а
 б
б
Рис. 3. Изолинии нормальных напряжений: а – σx; б – σz
 а
а
 б
б
Рис. 4. Функции компонентов деформации: а – εx; б – εz
Заключение
В работе определены напряженно-деформируемое состояние анизотропного (трансверсально-изотропного) пласта при фильтрации в нем жидкости. Установлена связь между напряжениями пласта и давлением фильтрирующейся жидкости. Численное решение поставленной задачи получено на основе МКЭ с применением изопараметрического элемента первого порядка. Представлена конечно-элементная модель напряженного деформируемого состояния пласта с горизонтальной скважиной произвольного профиля. Проанализированы пути определения упругих и фильтрационных характеристик деформируемых неоднородных пластов.
Таким образом, с помощью конечно-элементной модели можно получить оценку изменения давления жидкости в напряженно-деформируемом состоянии трансверсально-изотропного пласта.
Рецензенты:
Муратов А.С., д.т.н., профессор, заведующий кафедрой «Математика» Международного казахско-турецкого университета имени Х.А. Ясави Министерства образования и науки Республики Казахстан, г. Туркестан;
Ашибаев Н.К., д.ф.-м.н., профессор, заведующий кафедрой «Теория и методика преподавания математики» Южно Казахстанского государственного университета имени М. Ауезова Министерства образования и науки Республики Казахстан, г. Шымкент.
Работа поступила в редакцию 04.04.2014.
Библиографическая ссылка
Ажиханов Н.Т., Марасулов У.А. КОНЕЧНО-ЭЛЕМЕНТНАЯ МОДЕЛЬ ФИЛЬТРАЦИИ ЖИДКОСТИ К СКВАЖИНЕ В ДЕФОРМИРУЕМОМ ПЛАСТЕ // Фундаментальные исследования. 2014. № 6-1. С. 13-17;URL: https://fundamental-research.ru/ru/article/view?id=34099 (дата обращения: 09.01.2026).



