Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Бакин М.Н. 1 Капранова А.Б. 1 Верлока И.И. 1

---

1 ФГБОУ ВПО «Ярославский государственный технический университет»

Статья содержит результаты теоретического исследования механизма поведения частиц сыпучих компонентов при их смешивании после разбрасывания гибкими элементами вращающегося барабана в рабочем объеме устройства с подвижной лентой. Моделирование процесса смешивания зернистых сред выполнено с учетом геометрических особенностей расположения по винтовой линии билов на поверхности цилиндрических барабанов. Согласно стохастическому подходу для описания указанной технологической операции применяется теория ударных взаимодействий дисперсных систем. Построены дифференциальные функции распределения сыпучих компонентов в области их смешивания в зависимости от угла распыливания с учетом конструктивных и режимных параметров аппарата, а также физико-механических характеристик сред. Полученные результаты могут быть использованы при оценке качества зернистой смеси, например, по критерию в форме коэффициента ее неоднородности.

Статья в формате PDF

935 KB

смешивание

сыпучие материалы

математическое описание

стохастическая энергия частицы

дифференциальная функция распределения

угол распыливания

1. Дитрих Я. Проектирование и конструирование. Системный подход. – М.: Мир, 1981. – 456 с.

2. Протодьяконов Н.О. Статистическая теория явлений переноса в процессах химических технологии / Н.О. Протодьяконов, С.Р. Богданов. – Л.: Химия, 1983. – 400 с.

3. Бабуха Г.Л. Взаимодействие частиц полидисперсного материала в двухфазных потоках / Г.Л. Бабуха, А.А. Шрайбер. – Киев: Наукова думка, 1972. – 175 с.

4. Зайцев А.И. Ударные процессы в дисперсно-пленочных системах / А.И. Зайцев, Д.О. Бытев. – М.: Химия, 1994. – 176 с.

5. Капранова А.Б. Стохастическое описание движения осветленной фракции суспензии порошков / А.Б. Капранова, А.Е. Лебедев, Д.О. Бытев, А.И. Зайцев // Изв. ВУЗов. Химия и химическая технология. – Иваново, 2004. – Т. 47, вып. 6. – С. 99–101.

6. Исследование ударного смешивания твердых дисперсных сред при вторичных столкновениях частиц / А.Б. Капранова, М.Н. Бакин, А.Е. Лебедев, А.И. Зайцев // Изв. ВУЗов. Химия и химическая технология. – Иваново, 2013. – Т. 56, вып. 6. – С. 83–86.

7. Капранова А.Б. Расчет степени уплотнения порошка в шнековой машине с учетом проскальзывания и трения / А.Б. Капранова, А.И. Зайцев, Т.П. Никитина // Теор. основы хим. технологии. – 2000. – Т. 34, № 6. – С. 649–656.

8.Лебедев А.Е. Математическая модель механики движения сыпучих материалов в разреженных потоках аппаратов с эластичными рабочими элементами / А.Е. Лебедев, А.И. Зайцев, А.Б. Капранова, И.О. Кузьмин // Изв. ВУЗов. Химия и химическая технология. – Иваново, 2012. – Т. 52, вып. 5. – С. 111–113.

Формирование математической модели процесса смешивания сыпучих компонентов на ленте смесителя при вращении барабанов с эластичными элементами относится к необходимому этапу системно-структурного анализа [1] данной технологической операции при проектировании оборудования указанного назначения. Одним из наиболее эффективных способов описания механизма поведения зернистых сред при их смешивании в рабочем объеме аппарата с подвижной лентой является стохастический подход вследствие хаотичности движения частиц, составляющих смешиваемые компоненты [2]. В настоящей работе предлагается построение соответствующей модели движения сыпучих компонентов с помощью теории ударных процессов в дисперсных системах [3, 4], успешно применяемой в случаях разделения суспензий [5], смешивания твердых дисперсных сред при ударных взаимодействиях с отбойной поверхностью [6].

Цель работы: моделирование дифференциальных функций распределения сыпучих компонентов в рабочем объеме барабанно-ленточного смесителя с гибкими элементами, расположенными по винтовой линии на вращающихся относительно горизонтальных осей цилиндрических барабанах в зависимости от угла распыливания частиц.

Геометрические особенности рабочей области барабанно-ленточного смесителя сыпучих компонентов

Пусть дозируемые сыпучие среды условно первого и второго компонентов порознь подаются на горизонтальную движущуюся ленту таким образом, что первый материал покрывает данный транспортер, а второй – может подаваться порционно для получения заданного качества смеси с неравными массовыми долями составляющих, например 1:10 и более. Слои указанных твердых дисперсных систем проходят в барабанно-ленточный зазор и захватываются билами, закрепленными по винту (рис. 1) на вращающихся в различные стороны цилиндрических барабанах. Как навивка смесительных элементов на двух барабанах, так и вращение этой пары цилиндров осуществляются в противоположных направлениях, что способствует формированию рабочей области смешивания между указанными цилиндрическими поверхностями. Готовая сыпучая смесь оседает на транспортерную ленту и удаляется в зону выгрузки.

Рис. 1. Фото барабана с гибкими элементами, закрепленными по винтовой линии на его поверхности

В настоящем изложении ограничимся рассмотрением процесса смешивания зернистых компонентов в потоке частиц, подбрасываемых гибкими элементами одного барабана, вращающегося с угловой скоростью ω (рис. 2). Пусть длина каждого j-го била EjDj (j = 1, ..., nb) равна lb, их число – nb, радиус барабана – rb, его длина – Lb, шаг винтовой линии на цилиндрической поверхности барабана – hs, высота валково-ленточного зазора – h0. Согласно анализу предварительных экспериментальных исследований считается, что деформированные гибкие элементы восстанавливают свою форму при повороте барабана на угол π радиан. При рассмотрении движения частиц, составляющих сыпучие компоненты, в поперечной плоскости вращения барабана воспользуемся аналогией с плоско-деформационной моделью перемещения твердых дисперсных сред в сужающемся канале шнека [7]. Тогда представим уравнение спиральной кривой rs(θ) в указанной плоскости Oxy как геометрическое местоположение проекций концов Dj билов на эту плоскость в форме

(1)

где угол θ соответствует окружной координате цилиндрической системы координат с тем же направлением отсчета, что и угол θj = αj + φj для точки Dj (рис. 2). Последнее выражение с учетом (1) позволяет определить зависимость между углами θj и δj, показанными на рис. 2, а также перечисленными ранее конструктивными параметрами смесителя в следующем приближенном виде:

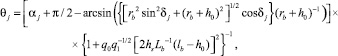(2)

где

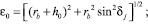
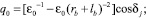
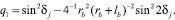
Заметим, что угол βj между полярной нормалью и радиус-вектором rj точки Dj вычисляется в соответствии с уравнением спиральной кривой (1) с помощью соотношения

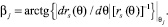(3)

Кинематический анализ движения частиц сыпучих компонентов

Проанализируем движение частицы сыпучего материала как i-го компонента получаемой смеси (i = 1, ..., nk) при ее отрыве от j-го гибкого элемента барабана смесителя (j = 1, ..., nb) в проекции на плоскость Oxy, перпендикулярную оси его вращения (рис. 3). Считая, что направление касательной к спиральной кривой rs(θ) совпадает с направлением проекций vxyij = vrθij вектора для абсолютной скорости движения 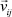указанной частицы, имеем

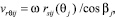(4)

где согласно (1) и (5) угол βj рассчитывается по формуле

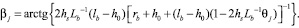(5)

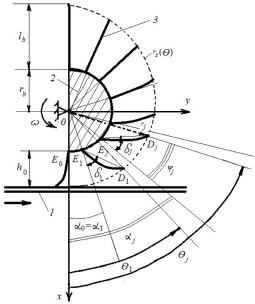
Рис. 2. Условная схема деформирования билов барабанно-ленточного смесителя: 1 – лента, 2 – барабан, 3 – бил

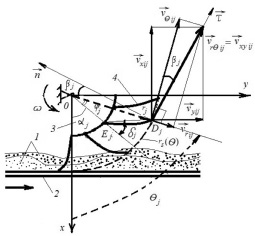
Рис. 3. Условная схема разложения скорости частицы i-го компонента при срыве с j-го била

Описание распределения частиц сыпучих компонентов в зависимости от угла их распыливания

В настоящей работе для описания процесса получения разреженных потоков движения частиц для смешиваемых зернистых компонентов предлагается использовать стохастический подход из теории ударных процессов [2, 3], развитый для течений жидких струй [4], разделения суспензий [5], смешивания сыпучих материалов при ударе об отбойник [6]. Пусть каждый поток i-го компонента смеси (i = 1, ..., nk) состоит из частиц, возможно влажных, произвольной формы с усредненной массой

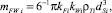
где kFi, kWi – соответственно коэффициенты формы и влажности, учитывающие, во сколько раз отличаются массы несферической и сферической (или влажной и невлажной) частиц; dSi – усредненный диаметр элементов пробы для i-го материала. Движение составляющих разреженных потоков i-го компонента смеси в поперечной плоскости Oxy (рис. 3) с учетом их слипаемости и отрыва от каждого j-го гибкого элемента барабана смесителя (j = 1, ..., nb) моделируется в фазовом пространстве с элементом

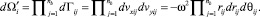(6)

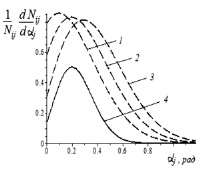
Рис. 4. Дифференциальные функции распределения числа частиц i-го компонента (песка ГОСТ 8735-88) по углу распыливания: пунктирные линии (1–3) – Fij(αj): 1 – j = 1; 2 – j = 2; 3 – j = 3; сплошная линия 4 – Φi(α1, α2, α3)

Однако, считая происходящие взаимодействия частиц i-го компонента с j-м гибким элементом, как независимые друг от друга, при построении модели их распределения в рабочем объеме барабанно-ленточного смесителя можно ограничиться описанием их движения в каждом из фазовых объемов вида dΩij с учетом, что кинематические характеристики (например, vxyij или vrθij) движений частиц сравнимы для различных компонентов (i = 1, ..., nk) в момент указанного отрыва от концов билов (j = 1, ..., nb) барабана

(7)

При этом убывание числа частиц i-го компонента в соответствующем разреженном потоке dNij после срыва с j-го била, происходящее в процессе образования зернистой смеси, представляется экспоненциальным относительно стохастической энергии Eij отдельно рассматриваемой частицы в описанном фазовом пространстве dΩij аналогично [4]

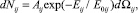(8)

где нормировочный коэффициент Aij задается выражением для числа частиц i-го материала, взаимодействующего с j-м гибким элементом

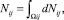(9)

а обобщенный энергетический параметр E0ij обычно вычисляется из закона сохранения энергии для характерного временного интервала [5, 6].

Определяя стохастическую энергию каждой составляющей потока i-го компонента при проецировании ее движения на плоскость Oxy, перпендикулярную оси вращения барабана (рис. 3), как сумму трех слагаемых – кинетических энергий поступательного и вращательного движений частицы, как и в работе [6], с учетом случайного характера ее момента импульсов 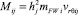при срыве с гибкого элемента, а также согласно подходу [8] – энергии этой частицы при упругом взаимодействии с билом, равной работе его сил упругости, имеем

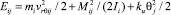(10)

при обозначениях:

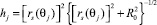
– кратчайшее расстояние от вектора 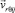до оси вращения барабана; 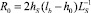; ku – угловой параметр жесткости била; 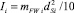– момент инерции для частицы массой mFWi и диаметром dSi.

Следовательно, учитывая (4), (5) для (10), справедливо

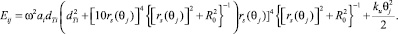(11)

Как уже отмечалось, для поиска Aij используется (9) в форме

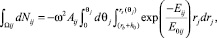(12)

тогда дифференциальная функция распределения сыпучего i-го компонента смеси (i = 1, ..., nk) при отрыве от j-го гибкого элемента смесителя (j = 1, ..., nb) в зависимости от угла распыливания частиц αj в поперечной плоскости Oxy (рис. 3) задается формулой

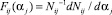(13)

или согласно (11) и (2) при интегрировании dNij в фазовом объеме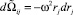

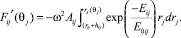(14)

Результаты исследования и их обсуждение

Подстановка (10) в (14) в соответствии с (2) и (13) приводит к выражению

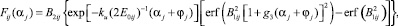(15)

где

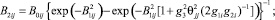
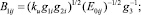
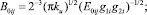
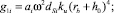
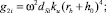
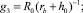
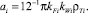
Тогда при выполнении (7) полная дифференциальная функция распределения сыпучего i-го компонента смеси (i = 1, ..., nk) по углу распыливания частиц αi (согласно (2) при 0 ≤ θj ≤ θDj) в поперечной плоскости Oxy (рис. 3) в его рабочем объеме при расположении билов по винтовой линии на вращающемся относительно горизонтальной оси цилиндрическом барабане (рис. 1) с учетом формы составляющих и возможной их влажности имеет форму

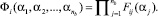(16)

Приведем в качестве примера на рис. 4 набор кривых, соответствующих полученным зависимостям из (15) и (16) в случае следующих значений: (1) конструктивных параметров rb = 3,0∙10–2 м; lb = 4,5∙10–2 м; h0 = 2,0∙10–2 м; hs = 3,0∙10–2 м; Lb = 1,85∙10–1 м; ku = 5,0∙10–4 кг∙м/рад при nb = 3 – числе билов (j = 1, ..., nb) с поворотом барабана на угол π/2 рад; (2) режимного показателя ω =47,12 рад/c; (3) физико-механических характеристик одного из смешиваемых компонентов – песка ГОСТ 8735-88 (i = 1, ..., nk): kF1 = 1,0; kW1 = 1,0; dS1 = 1,5∙10–4 м; ρT1 = 1,525∙103 кг/м3.

Заключение

Таким образом, построенная модель смешивания в его рабочем объеме барабанно-ленточного аппарата с расположением билов по винтовой линии в поперечной плоскости вращения барабана имеет следующие особенности: применима при смешивании нескольких сыпучих компонентов без традиционного деления на ключевой и транспортирующий материалы; определяет дифференциальные функции распределения смешиваемых компонентов и смеси по углам распространения потоков с учетом формы твердых частиц и их возможной влажности.

Приведенные результаты моделирования позволяют сформировать дифференциальную функцию распределения смешиваемых компонентов в продольной плоскости движения частиц их разреженных потоков по другим координатам – x и z; провести оценку качества смеси, например, при расчете ее коэффициента неоднородности.

Рецензенты:

Бачурин В.И., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Ярославского филиала ФГБОУ ВПО «Московский государственный университет путей сообщения (МИИТ)», г. Ярославль;

Ефремов Г.И., д.т.н., профессор, заведующий кафедрой «Проектирование технологических машин и комплексов в химической промышленности», ФГБОУ ВПО «Московский государственный машиностроительный университет (МАМИ)», г. Москва.

Работа поступила в редакцию 26.03.2014.

Библиографическая ссылка