Проблема математического моделирования процесса смешивания сыпучих материалов не теряет своей актуальности, что объясняется широким кругом задач проектирования оборудования по переработке указанных сред для самых различных целей во многих отраслях промышленности [1–5].
Цель работы: разработать условную классификацию современных методов математического моделирования процессов смешивания сыпучих материалов и дать краткое описание наиболее распространённых методов.
Классификация математических моделей процессов смешивания сыпучих материалов
При формировании математической модели процесса смешивания сыпучих сред необходимо провести анализ поведения твердой дисперсной системы (обычно многокомпонентной или многофазовой) с двух позиций, называемых как уровни микро- и макро-. При этом моделирование возможно в нескольких направлениях: (а) только на макроуровне (в рабочей камере аппарата); (б) на макроуровне с учетом специфических особенностей поведения частиц в пределах микроуровня (т.е. при смешивании в локальной области). Условная классификация математических моделей процессов смешения сыпучих материалов представлена на рисунке. В последнее десятилетие наибольшую значимость по сравнению с традиционными детерминированными моделями (регрессии, структуры потока, теории управления, конвекции и т.д.), классифицированными по различным признакам в работах [3–7], приобретают индетерминированные (вероятностные) способы описания смешивания сыпучих компонентов.
Детерминированные модели
Как правило, детерминированные модели соответствуют аналитическому описанию поведения исследуемой системы при условии однозначности сформированной функциональной зависимости с заданными входными параметрами. Построение таких функций в случае смешивания сыпучих компонентов значительно осложняется многофакторностью задачи вследствие необходимости учета физико-механических параметров (для материалов смеси) и конструктивно-режимных параметров (для проектируемого вида смесительного оборудования).
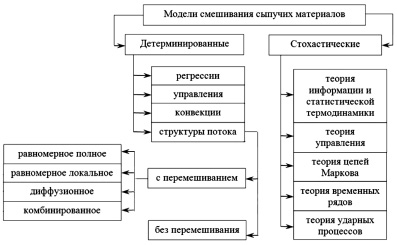
Классификация математических моделей процессов смешивания сыпучих материалов
А. Модели регрессии. Данные модели основаны на множестве результатов предварительных испытаний модельных опытных смесителей выбранного типа. Экспериментальные исследования позволяют выбрать наиболее значимые факторы, влияющие на изучаемый процесс в конкретном виде смесительного аппарата при построении регрессионной кривой для функции показателя качества смеси (например, коэффициента ее неоднородности [1]) от набора учитываемых параметров процесса смешивания. При этом опытным данным ставятся в соответствие регрессионные уравнения, описывающие указанные кривые. Обычно такие зависимости представляются в удобной для проведения анализа форме – с привлечением критериев подобия, характеризующих учет наиболее значимых эффектов, которые наблюдаются в процессе смешивания сыпучих компонентов в конкретном устройстве для пределов изменения характеристических параметров аппарата, определенных условиями опытов [1]. Применение моделей регрессии возможно для различных типов смесителей (механических, вибрационных, пневматических) и видов смешиваемых материалов (полимерных, пищевых, увлажненных сред и т.д.). При этом практически невозможен механический перенос полученных результатов модели на более широкий диапазон характеристических параметров.
Б. Модели структуры потока. Описание смешивания сыпучих компонентов может быть проведено согласно [1] с точки зрения отсутствия перемешивания потоков материалов или его наличия в зависимости от способа реализации:
1) полное равномерное во всем объеме (идеальная модель);
2) локальное равномерное в выделенной ячейке (ячеечная модель);
3) диффузионное в поперечном и (или) продольном направлениях;
4) комбинированное из перечисленных.
Условно смешиваемые компоненты разделяются на два основных потока: ключевой (один из множества материалов как наименее инертный) и транспортирующий (один материал или набор нескольких реальных сред). Модели содержат дифференциальные уравнения, описывающие изменение с течением времени концентрации ключевого компонента. Применяются в основном ячеечные или комбинированные модели, т.к. реализация идеального смешивания требует нулевых значений степени неоднородности и времени смешения, а идеального вытеснения – наличия отличных друг от друга физико-механических свойств для ключевой и транспортирующей составляющих смеси.
Диффузионные детерминированные модели предполагают неоднозначный выбор метода оценки коэффициента макродиффузии, как правило, экспериментальный. Однако имеются работы, совмещающие при построении диффузионной модели детерминированный и вероятностный подходы. С одной стороны, базовые уравнения являются классическими для массообменных процессов, а с другой – поиск параметра макродиффузии производится с помощью стохастического моделирования. Ячеечный подход – для исследования непрерывных режимов работы смесителей или при наличии циркуляционных потоков в замкнутом контурном объеме, а комбинированный – для описания смешивания в рабочих камерах с застойными областями или баспайными, циркуляционными потоками. Основные недостатки данных моделей:
а) не учитывают особенности смешивания сыпучих сред, т.е. возможность проявления эффектов сегрегации, агломерации, конвективного перемешивания;
б) имеют опосредованную связь с конструктивно-режимными параметрами смесителя, выявление которой крайне трудоемко при решении задач оптимизации.
В. Модели теории управления. Кибернетический подход базируется на теории управления автоматизированными системами. При этом считается, что исследователем может быть сформировано два набора параметров, характеризующих состояние перерабатываемой дисперсной системы в смесителе-преобразователе «условного сигнала» – на входе x(t) и на выходе y(t). Постулирование передаточной функции w(ζ) стационарного линейного преобразования относительно комплексной переменной ζ, которая отражает механизм поведения смешиваемых компонентов, позволяет с помощью оператора Лапласа установить функциональную зависимость, применяемую для прогнозирования процесса смешивания сыпучих материалов. К позитивным особенностям таких моделей можно отнести возможность их применения для проектирования смесителей:
1) с учетом способа дозирования сыпучих компонентов в форме отражения на исследуемый процесс в наборе входных параметров;
2) с различными режимами работы (непрерывным, периодическим, рециркуляционным) [2]. Однако данный метод не справляется с определением показателя неоднородности сыпучей смеси вследствие эффекта агломерации составляющих частиц, а также требует сравнительного анализа с регрессионными моделями с целью верификации.
Г. Модели теории конвекции. Применение уравнений гидродинамического типа к описанию движения механической системы с хаотическими смещениями позволяет при разложении их кинематических характеристик в двойной ряд Фурье перейти к другой постановке, называемой задачей аттрактора Лоренца с помощью трех специальных параметров (σ, r, b), когда фазовые переменные (x, y, z) соответствуют скоростным показателям. Некоторые модели теории конвекции описывают формирование слоев сыпучей смеси посредством геометрических преобразований исходного объема компонентов. Кроме того, имеются модели, объединяющие элементы конвективного и диффузионного подхода.
Стохастические модели
Индетерминированные модели для процесса смешивания сыпучих материалов соответствуют стохастическому подходу, когда в связи с хаотичным характером изучаемого процесса конечное состояние системы не может быть однозначно задано ее начальным.
А. Модели теории информации и статистической термодинамики приводят к описанию процесса смешивания сыпучих компонентов с помощью информационной энтропии. Согласно определению К. Шеннона информационная энтропия характеризует неупорядоченность изучаемой информационной системы. Известный закон сохранения суммы информации и энтропии (как их суммы, равной исходной неопределенности) подразумевает, что получение всей полезной информации приводит к нулевой неопределенности (неупорядоченности) системы. В случае статистической термодинамики уменьшение энтропии Больцмана соответствует переходу термодинамической системы из более вероятного состояния в менее вероятное, т.е. возрастание данного показателя наблюдается для значительных временных промежутков. Глубокая связь между понятиями энтропии из теории информации и статистической механики позволяет описать состояние смеси с равными массовыми долями компонентов через максимальное значение информационной энтропии. Согласно анализу [3, 5] принимается допущение о формальном равенстве значений массовой доли выделенного компонента в составе идеальной смеси вероятности обнаружить данную дисперсную составляющую в готовом продукте смешения. Качество смеси предлагается оценивать с помощью параметра эффективности смешивания. Применение энтропийно-информационных моделей является наиболее оправданным в случае получения смеси из компонентов со значительным расхождением их массовых долей в составе (например, 1:100, 1:1000 и более). Недостаток модели – затруднительность учета особенностей движений сред при расчете вероятностных показателей процесса.
Б. Модели теории управления. Данный подход к описанию процесса смешивания сыпучих материалов имеет некоторые общие идеи с кибернетическим методом моделирования, т.к. для получения «выходного сигнала» смесительное оборудование также предполагается рассматривать в форме преобразователя «входного возмущения». Основной целью является получение функции распределения времени пребывания (ФРВП) частиц смешиваемых компонентов в рабочей камере устройства, которая строится по кривой отклика. Однако подбор введенных в ФРВП констант осуществляется по опытным данным для конкретных устройств, что существенно затрудняет учет механизма перемешивания сыпучих компонентов в рабочей камере оборудования и перенос результатов моделирования на расширенные пределы изменения конструктивно-режимных параметров смесителя [7].
В. Модели цепей Маркова. Обычно случайные процессы описываются кинетическими уравнениями относительно условных вероятностей событий. Разделяют следующие режимы протекания случайного процесса: дискретный и непрерывный. Условно такие процессы классифицируются по признаку причинности связи между событиями и разделяются соответственно на два вида операций:
а) без корреляций между событиями (с полностью независимыми значениями);
б) в зависимости только от мгновенных состояний системы (без «предыстории» события – марковские процессы). Например, в [3–6] используется метод цепей Маркова, когда плотности вероятности непрерывного случайного процесса от состояний и времени имеют смысловую нагрузку функции удельной концентрации ключевого компонента. В зависимости от режимов протекания операции смешения можно выделить несколько способов построения моделей указанного типа: диффузионный с учетом изменения концентраций компонентов смеси под действием заданного силового поля; кинетический в соответствии с параметром скорости смешивания и значениями дисперсии распределения концентраций каждого сорта частиц; рождения-гибели для описания совмещенных процессов измельчения и смешивания сыпучих сред с помощью системы дифференциально-разностных уравнений Колмогорова; оценки изменения моментов распределения и т.д. В частности, известны модели с последовательным делением материала на подслои с ячейками со скачкообразным характером изменения концентрации ключевого компонента [4, 8] или с заданием распределения массового количества продукта в матричной форме с элементами в виде вероятностей перемещаемых частиц из одной области в другую.
Г. Модели теории временных рядов предполагают наличие сложной структуры потоков компонентов в виде элементарных временных составляющих трендов, описание поведения которых проводится с помощью суперпозиции моделируемых функций полиномов, тригонометрических зависимостей с учетом цикличности изменений случайных величин. Как показано в [3], результаты моделирования относятся к построению корреляционных функций и других характеристик случайного процесса смешивания.
Д. Модели теории ударных процессов в дисперсных системах, развитые для течений жидких струй [5], разделения суспензий, применяются для смешивания сыпучих материалов при ударе об отбойник [6, 9]. При этом моделируются дифференциальные функции распределения твердых сферических частиц каждого компонента по их диаметрам [6] (при слипаемости или дроблении) или углу распыливания [9] после отрыва от радиальных билов смесительного барабана. Формирование стохастической энергии частицы в фазовом пространстве каждого сыпучего потока (совокупности одной компоненты скорости центра масс и ее диаметра [6] или ее случайного импульса и угла распыливания [9]) проводится с учетом случайного характера моментов импульсов компонентов при вторичных столкновениях частиц [6] или коэффициента жесткости эластичного элемента [9]. Считается, что при смешивании происходит экспоненциальное убывание числа частиц для каждого из потоков. Модели позволяют рассчитать коэффициент неоднородности смеси, но не учитывают форму частиц компонентов.
Выводы
Анализ литературных источников, относящихся к современным методам описания смешивания сыпучих материалов на подвижной ленте, показал перспективность стохастической направленности моделей с учетом особенностей конкретного смесителя, отсутствие моделей смешивания на подвижной ленте при порционном (постепенном) внесении одного из компонентов смеси в другой, возможность эффективного описания данной операции с помощью теории ударных процессов.
Рецензенты:
Бачурин В.И., д.ф.-м.н., профессор кафедры «Высшая и прикладная математика» Ярославского филиала ФГБОУ ВПО «Московский государственный университет путей сообщения (МИИТ)», г. Ярославль;
Ефремов Г.И., д.т.н., профессор, заведующий кафедрой «Проектирование технологических машин и комплексов в химической промышленности», ФГБОУ ВПО «Московский государственный машиностроительный университет (МАМИ)», г. Москва.
Работа поступила в редакцию 21.03.2014.
Библиографическая ссылка
Бакин М.Н., Капранова А.Б., Верлока И.И. СОВРЕМЕННЫЕ МЕТОДЫ МАТЕМАТИЧЕСКОГО ОПИСАНИЯ ПРОЦЕССА СМЕШИВАНИЯ СЫПУЧИХ МАТЕРИАЛОВ // Фундаментальные исследования. 2014. № 5-5. С. 923-927;URL: https://fundamental-research.ru/ru/article/view?id=34019 (дата обращения: 28.02.2026).



