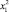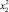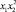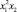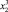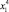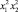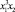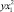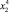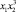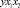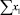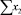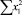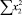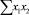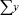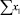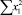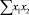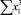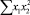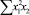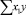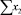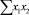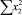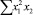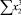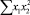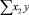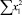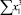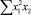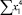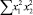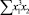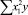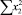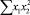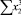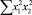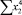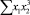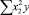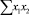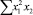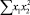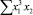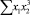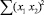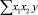Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Адамадзиев К.Р. 1 Адамадзиева А.К. 1

---

1 ФГБОУ ВПО «Дагестанский государственный университет»

Предметом исследования являются связи и зависимости между социально-экономическими показателями регионов. Сформулирована задача, в соответствии с которой требуется выявить зависимость ВРП от численности занятых в экономике и стоимости основных фондов, и построены уравнения регрессии в виде полинома второго порядка, апробированные по данным 27 малых регионов России по величине ВРП за 2010 г. Описаны два разных способа определения параметров и статистических характеристик многофакторных полиномиальных уравнений регрессии с помощью различных функций, процедур и средств MS Excel. Дана авторская методика расчета параметров и характеристик двухфакторных моделей регрессии полиномиального вида и оценка результатов. Разработана и описана компьютерная модель, позволяющая автоматизировать все необходимые расчеты и процедуры обработки информации и строить как полные, так и неполные варианты полиномиальных уравнений регрессии. Дана сравнительная оценка различных вариантов двухфакторных полиномов второго порядка, построенных по данным малых регионов с помощью ключевых статистических характеристик, и определены наиболее значимые из уравнений.

Статья в формате PDF

733 KB

методика

зависимости

экономика

таблица-шаблон

модель

полином

регрессия

параметры

статистические характеристики

1. Адамадзиев К.Р., Адамадзиева А.К. Оценка зависимости ВРП от инвестиций, численности занятых в экономике и стоимости основных фондов с помощью моделей панельных данных (на примере регионов России) // Международный журнал прикладных и фундаментальных исследований. – 2011. – № 9. – С. 68–70.

2. Лавренов С.М. Excel: Сборник примеров и задач. – М.: Финансы и статистика, 2008. – 336 с.

3. Математическое и компьютерное моделирование экономики регионов. 20 фев. 2011 ... III Студенческий научный форум (15–20 февраля 2011 года) rae.ru/forum2011/164.

4. Практикум по эконометрике: под ред. И.И. Елисеевой. – 2-е изд., перераб. и доп. – М.: Финансы и статистика, 2008. – 344 с.

5. Россия в цифрах, 2011: Крат. Стат. Сб. / Росстат. – М., 2011. – 581 с.

6. Эконометрика: учебное пособие в схемах и таблицах; под ред. д-ра экон. наук, проф. С.А. Орехова. – М.: Эксмо, 2008. – 224 с.

Важнейшими функциями, выполняемыми на любых экономических объектах, являются аналитические функции, которые, как правило, выполняются работниками среднего и высшего уровня управления. При проведении анализа часто возникает необходимость в проведении множества расчётов и процедур обработки информации. Для автоматизации расчётов и процедур обработки информации в настоящее время разработаны и применяются так называемые BI-системы (аналитические системы подготовки принятия решений).

К числу наиболее значимых задач для BI-систем можно отнести задачи, в которых требуется количественно выразить и оценить связи и зависимости между различными экономическими показателями и тенденции их изменения.

Особенность таких задач состоит в том, что связи, зависимости и тенденции носят неопределённый, вероятностный характер для любого из выбранных совокупностей и поэтому не могут быть однозначно определены. Во-первых, зависимость даже между одними и теми же показателями для одной и той же совокупности может быть описана разными видами уравнений регрессии (как линейными, так и нелинейными); во-вторых, удаление любого из объектов совокупности или добавление нового объекта в состав исследуемой совокупности может изменить степень тесноты связи и её характеристики.

Содержание

Связи и зависимости между экономическими показателями могут быть описаны одно- и многофакторными моделями регрессии. Особое место среди видов моделей регрессии занимают модели, описываемые полиномами второго порядка. Уже однофакторная модель такого вида, записываемая в виде уравнения параболы, отличается от остальных однофакторных тем, что, во-первых, она содержит три параметра (а не два, как, например, линейное, показательное и степенное); во-вторых, на ее основе можно определить величину показателя-фактора, при котором результативный показатель принимает максимальное (или минимальное) значение.

Так, если однофакторное уравнение параболы записать в виде

y = b + m1x + m2x2,

то при 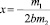y принимает max или min.

При этом сама величина ymax (ymin) равна

.

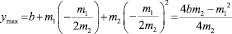Т.о., точка max (min) – это вершина параболы, координаты которой равны .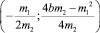

Двухфакторная полиномиальная модель регрессии параболического вида в общем случае представляет собой уравнение, которое имеет следующую математическую запись:

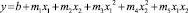.(1)

Методика расчёта параметров этого уравнения аналогична методике построения пятифакторного уравнения линейного вида:

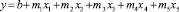. (2)

Параметры уравнения (1) можно рассчитать методом наименьших квадратов, в соответствии с которым требуется составить и решить систему нормальных уравнений [4, 6].

Поскольку с помощью уравнений регрессии выявляются и оцениваются приближенные траектории связей и зависимостей, называемые корреляционными, то для обоснования их адекватности и возможности практического применения принято рассчитывать статистические характеристики.

На основе учебной литературы по эконометрике [2, 4, 6] нами разработан модельный инструментарий, включающий комплекс из 20 формул.

Особенности построения двухфакторных уравнений параболического вида (см. формулу (1)) и методика оценки связей и зависимостей с их помощью рассмотрим на конкретном практическом примере.

Пусть требуется построить двухфакторное уравнение регрессии для зависимости ВРП (y, млрд руб.) от численности занятых в экономике (х1, тыс. чел.) и стоимости основных фондов (х2, млрд руб.) для 27 малых регионов России по величине ВРП за 2010 г.

Для формирования выборки из 27 малых регионов достаточно создать в MS Excel таблицу с тремя рассматриваемыми показателями для всех регионов России [5], расположить регионы в порядке возрастания величины ВРП, а затем выбрать требуемые 27 регионов (табл. 1).

Таблица 1

Исходные данные по 27 малым регионам России за 2010 г. (фрагмент)

Чтобы рассчитать параметры уравнения с помощью системы нормальных уравнений требуется создать таблицу-шаблон (табл. 2) с исходными данными, предусматривающую выполнение всех необходимых промежуточных расчётов.

В строке «сумма» таблицы-шаблона 2 содержатся все величины (⅀y, ⅀x1, ⅀x2, …, ⅀(x1x2)2, ⅀x1x2y), необходимые для расчета параметров уравнений путем построения и решения системы нормальных уравнений.

Для выполнения промежуточных расчётов по таблице-шаблону (табл. 2) требуется:

а) ввести исходные значения y, x1, x2, в столбцы 2, 3 и 4;

б) в ячейки первой строки столбцов 6,7,…22 ввести с клавиатуры формулы: « = x12» , « = x22», « = x1x2,…», …, « = x1x2y» (см. выражения в столбцах табл. 2);

в) копировать формулы, введённые в ячейки первой строки, в ячейки всех остальных строк (кроме строки «сумма»);

г) в ячейку 2-го столбца строки «сумма» ввести формулу « = сумм» и скопировать её в остальные ячейки этой строки.

Подставив суммы из табл. 2 в систему нормальных уравнений, получим численную модель этой системы, содержащую шесть уравнений и шесть переменных, параметры которых можно рассчитать в MS Excel двумя способами:

а) с помощью процедуры «Поиск решения…»;

б) с помощью встроенной статистической функции «ЛИНЕЙН».

Таблица 2

Фрагмент таблицы-шаблона для расчета суммарных, средних и других промежуточных величин, необходимых для расчета параметров и статистических характеристик 2-факторных уравнений регрессии параболического вида

Продолжение табл. 2

Окончание табл. 2

Рассмотрим методику расчета параметров каждым способом. При применении первого способа создается пустая таблица-шаблон вида табл. 3 и в ее ячейки вводятся численные значения необходимых сумм из таблицы-шаблона 2. Ввод данных можно выполнить с клавиатуры, но лучше с помощью операторов присвоения, связывающих ячейки строки «сумма» и ячейки таблицы-шаблона 3. Это позволяет впоследствии автоматизировать все расчетные операции и процедуры обработки информации с помощью единой компьютерной модели.

При применении первого способа параметры уравнения выводятся в строку «решение» созданной таблицы-шаблона (табл. 3).

Mетодика расчета параметров с помощью процедуры «Поиск решения…» включает следующую последовательность действий:

– в рабочем окне MS Excel создается исходная таблица (которую принято называть расширенной моделью или числовой моделью решаемой задачи) в виде вышеприведенной табл. 3;

– в первую ячейку столбца «Расчетные выражения» вводится расчетное выражение, позволяющее перемножить элементы 1-й строки на элементы строки «решение» (используя встроенную математическую функцию «СУММПРОИЗВ» из MS Excel);

– аналогичные расчетные выражения вводятся (копируются) во все строки столбца «Расчетные выражения», включая строку «целевая функция»;

– установив курсор на ячейку на пересечении строки «целевая функция» и столбца «расчетные выражения», запускается процедура «Поиск решения…» и в появившемся окне выполняются предусмотренные действия: выбор целевой ячейки; указание адресов ячеек, в которые выводится решение; ввод ограничений; нажатие кнопки «выполнить»; (после вывода сообщения «задача решена») нажатие клавиши «ОК».

Таблица 3

Таблица-шаблон для расчёта параметров двухфакторных уравнений регрессии параболического вида с помощью процедуры «Поиск решений…»

Результаты расчетов с помощью процедуры «Поиск решения…» выводятся в ячейки строки «решение» табл. 3.

По данным табл. 3 можно рассчитывать параметры не только двухфакторных моделей регрессии для полного полинома, но и следующих частных вариантов полиномов:

2) у = b + m₁x₁ + m₂x₂ + m₃x₁²;

3) у = b + m₁x₁ + m₂x₂ + m₄x₂²;

4) у = b + m₁x₁ + m₂x₂ + m₅x₁х₂;

5) у = b + m₁x₁ + m₂x₂ + m₃x₁² + m₄x₂²;

6) у = b + m₁x₁ + m₂x₂ + m₃x₁² + m₅x₁х₂;

7) у = b + m₁x₁ + m₂x₂ + m₄x₂² + m₅x₁х₂.

Для аналитических целей параметры, рассчитанные по уравнениям регрессии всех семи видов, целесообразно свести в табл. 4.

Таблица 4

Величины параметров двухфакторного полиномиального уравнения регрессии для зависимости ВРП от численности занятых в экономике и стоимости основных фондов, построенного по данным 27 малых регионов России за 2010 г.

Как было отмечено выше, для оценки приемлемости построенных уравнений регрессии следует рассчитать ряд статистических характеристик.

В табл. 5 приведены данные, иллюстрирующие методику расчета двух наиболее значимых из статистических характеристик: коэффициента детерминации (R) и средней ошибки аппроксимации (А). Эта же таблица иллюстрирует промежуточные расчеты, которые для этого требуется выполнить (определить для каждого из уравнений регрессии расчетные значения (уx), а также

∑(у – у_x)² и ∑(у – у_ср)²).

Рассмотрим методику расчета параметров и статистических характеристик для двухфакторного полинома с помощью встроенной статистической функции «ЛИНЕЙН» (т.е. вторым способом).

В этом случае величины параметров и ряд дополнительных статистических характеристик рассчитываются и выводятся в виде следующей таблицы-шаблона, первая строка которой содержит величины параметров, вторая строка – их стандартные ошибки, остальные три – содержат шесть статистических характеристик. Их сущность и методику расчета см., например, в [2].

Таблица 5

Фрагмент таблицы, иллюстрирующей методику расчета статистических характеристик (индекса корреляции и средней ошибки аппроксимации) для двухфакторных полиномиальных моделей регрессии

Продолжение табл. 5

Окончание табл. 5

Особенность этой методики состоит в том, что для расчетных значений создается таблица–шаблон в виде таблицы 6. При этом количество столбцов в таблице равно числу параметров уравнения, а количество строк равно пяти. В частности, для расчета параметров и характеристик полного полинома 1 создается таблица-шаблон размерности 6×5 (см. табл. 6).

Таким образом, чтобы рассчитать параметры и статистические характеристики полиномиальной модели вторым способом требуется:

– создать таблицу-шаблон (табл. 6);

– активировать процедуру «Мастер функции…», в первом его окне выбрать категорию «статистические», а затем (во втором окне «Мастера функции») – встроенную функцию «ЛИНЕЙН»;

– выполнить во 2-м окне предусмотренные в нем действия, а именно: выбор «известных значений у», выбор «известных значений х», конст., статистика – и нажать клавишу «ОК»;

– нажать комбинацию клавиш Shift + Ctrl + Enter.

В таком виде таблица 6 неудобна для анализа. Поэтому на её основе целесообразно создать одну или несколько аналитических таблиц-шаблонов. В частности, для сравнительной оценки ключевых статистических характеристик двухфакторных полиномов второго порядка нами создана аналитическая табл. 7.

Таблица 6

Величины параметров и статистических характеристик для двухфакторных уравнений регрессии полиномиального вида для зависимости ВРП от численности занятых в экономике и стоимости основных фондов, построенных по данным 27 малых регионов России по данным за 2010 г.

Таблица 7

Величины ключевых статистических характеристик различных вариантов двухфакторных полиномов второго порядка, выражающих зависимость ВРП от численности занятых в экономике и стоимости основных фондов по данным 27 малых регионов России за 2010 г.

Как видно из табл. 7, практически все семь вариантов полиномов второго порядка оказались приемлемыми для оценки исследуемой зависимости, поскольку минимальные и максимальные значения величин трех статистических характеристик различаются по вариантам весьма незначительно: от 13,3 до 13,9 (sey), от 0,8796 до 0,8804 (r2), от 18,0 до 18,8 (A).

Ниже приведены три наиболее значимых из построенных нами вариантов полиномиальных уравнений регрессии:

а) 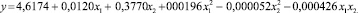– полный полином 2-го порядка (1 вариант);

б) 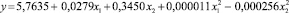– вариант, наиболее близкий к полному полиному (5-й вариант);

в) 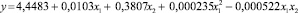. – наиболее приемлемый вариант по статистическим характеристикам (6-й вариант).

Все операции, связанные с выполнением расчетов и процедурами обработки информации, нами сведены в единую компьютерную модель, которая апробирована на примере 27 средних и 25 крупных регионов России за 2010 г.

Рецензенты:

Кутаев Ш.К., д.э.н., зав. отделом Воспроизводства населения и трудовых ресурсов Института социально-экономических исследований Дагестанского научного центра, г. Махачкала;

Алиев М.А., д.э.н., профессор кафедры экономической теории, ФГБОУ ВПО «Дагестанский государственный педагогический университет», г. Махачкала.

Работа поступила в редакцию 23.03.2014.

Библиографическая ссылка