Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,685

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Николаев А.П. 1 Киселёв А.П. 1 Гуреева Н.А. 1 Киселёва Р.З. 1 Леонтьева В.В. 1

---

1 ФГБОУ ВПО «Волгоградский государственный аграрный университет»

Для определения напряженно-деформированного состояния в зонах пересечения произвольно нагруженных оболочек вращения из разнородных материалов на основе метода конечных элементов используется ранее разработанный объемный шестигранный конечный элемент с узловыми неизвестными в виде перемещений и их производных. Для конечных элементов, примыкающих к границе сочленения оболочек вращения, получены соотношения между узловыми неизвестными одной оболочки, принятой за основную, и узловыми неизвестными другой оболочки, примыкающей к основной. На основе полученных соотношений выполнены преобразования матриц жесткости и векторов узловых нагрузок конечных элементов, примыкающих к границе сочленения оболочек из разнородных материалов. На основе анализа результатов расчета можно сделать вывод о корректности алгоритма определения напряженно-деформированного состояния в зонах сочленения оболочек вращения при произвольном нагружении.

Статья в формате PDF

1499 KB

МКЭ

произвольно нагруженные оболочки

объёмный шестигранный конечный элемент

узловые неизвестные

условия на границе пересечения оболочек

разнородный материал

1. Голованов А.И., Тюленева О.Н., Шигабудинов А.Ф. Метод конечных элементов в статике и динамике тонкостенных конструкций. – М.:Физматлит, 2006. – 392 с.

2. Бате К.Ю. Методы конечных элементов. – М.: Физматлит, 2010. – 1022 с.

3. Николаев А.П., Клочков Ю.В., Киселев А.П., Гуреева Н.А. Расчет оболочек на основе МКЭ в двумерной постановке. – Волгоград, 2009. – 194 с.

4. Киселев А.П. Векторная аппроксимация полей перемещений объемного шестигранного конечного элемента // Строительная механика инженерных конструкций и сооружений. – 2007. – № 1.

5. Киселев А.П. Объемный конечный элемент в виде треугольной призмы с первыми производными узловых перемещений / А.П. Киселев, А.П. Николаев // Изв. Вузов, сер. «Строительство». – 2006. – № 1. – С. 13–18.

6. Гуреева Н.А. Восьмиугольный конечный элемент в смешанной формулировке на основе функционала Рейснера // МБТУ им.Баумана, Известия вузов: Машиностроение. – № 5. – С. 23–28.

7. Гуреева Н.А. Расчет многослойной оболочки с использованием объемного конечного элемента / Н.А. Гуреева, А.П. Киселев, Р.З. Киселева // Известия ВолгГТУ. – Волгоград, 2010. – № 4. – С. 125–128.

8. Киселев А.П. Расчет многослойных оболочек вращения и пластин с использованием объёмного конечного элемента / А.П. Киселев, Н.А. Гуреева, Р.З. Киселёва // Изв. Вузов, сер. «Строительство». – 2010. – № 1. – С. 106–112.

9. Киселёв А.П. Использование трёхмерных конечных элементов в расчётах прочности многослойных панелей / А.П. Киселев, Н.А. Гуреева, Р.З. Киселёва // Строительная механика инженерных конструкций и сооружений. – 2009. – № 4. – С. 37–40.

10. Седов А.И. Механика сплошной среды. – М:. Наука, 1976. – т. 1,535.

Из-за сложности решения дифференциальных уравнений, описывающих деформированное состояние оболочек вращения, большое распространение получили численные методы определения их напряженно-деформированного состояния. Среди численных методов особое место занимает метод конечных элементов (МКЭ) в различных формулировках: в формулировке метода перемещений разрабатывались конечные элементы в двумерной постановке [1, 2, 3] и в трехмерной постановке [4, 5]; в смешанной формулировке использовались объемные конечные элементы [6]. Объемные конечные элементы в формулировке метода перемещений успешно использовались для расчета слоистых конструкций [7, 8, 9].

В настоящей работе для расчета произвольно нагруженной оболочки вращения в координатной системе s, θ, ζ используется шестигранный восьмиузловой конечный элемент с узлами i, j, k, l на нижней грани по координате ζ и узлами m, n, p, h по верхней грани [4].

Используемая в настоящей работе матрица жесткости объёмного шестигранного конечного элемента формируется на основе равенства работ внешних и внутренних сил [4, 5] и представляется выражением

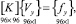(1)

где 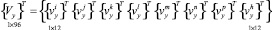– вектор узловых неизвестных в криволинейной системе координат s, θ, ζ;

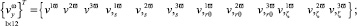
(ϖ = i, j, k, l, m, n, p, h) [K] – матрица жесткости элемента в глобальной системе координат; {f} – вектор узловых нагрузок элемента в глобальной системе координат.

1. Геометрия оболочки вращения в узловой точке. Положение произвольной точки М срединной поверхности произвольно нагруженной оболочки вращения в декартовой системе координат xoz определяется радиус-вектором (рис. 1)

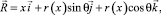(2)

где r = r(x) – радиус вращения точки М относительно оси ox; 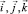– орты декартовой системы координат; θ – угол, отсчитываемый от вертикального диаметра против часовой стрелки.

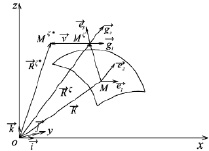
Рис. 1. Перемещение точки в результате деформирования оболочки из положения Mζ в положение Mζ*

Векторы локального базиса точки М определяются выражениями

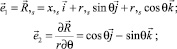
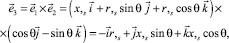(3)

где – производная радиуса вращения по дуге меридиана s.

Соотношения (3) можно представить в матричном виде

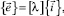
где 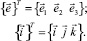(4)

Производные векторов локального базиса определяются дифференцированием (3) и с учетом (4) представляются в матричном виде

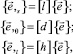(5)

где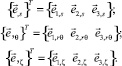

Радиус-вектор произвольной точки оболочки Mζ, отстоящей на расстоянии ζ от срединной поверхности, можно представить выражением

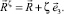(6)

Базисные векторы точки Mζ определяются дифференцированием (5)

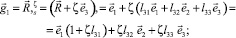
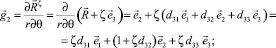(7)

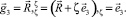
Произвольная точка Mζ оболочки под действием заданной нагрузки займет положение Mζ*, которое определяется вектором с компонентами в базисе точки M срединной поверхности

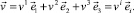(8)

Производные вектора перемещения по координатам s, r, θ, ζ с учётом (5) имеют вид

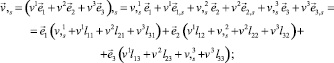
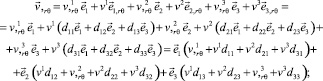
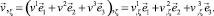(9)

Деформации в точке Mζ* определяются выражениями

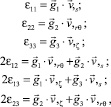(10)

которые можно представить для узловой точки в матричном виде

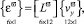(11)

где 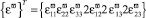– вектор – строка компонент деформаций в узловой точке оболочки.

Связь между напряжениями и деформациями определяется соотношениями механики сплошной среды [10]

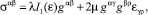(12)

где λ, μ – параметры Ламе;

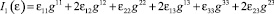
– первый инвариант тензора напряжений; gmn, gmn – ковариантные и контравариантные компоненты метрического тензора.

Зависимость (12) для узловой точки можно представить в виде

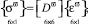(13)

где .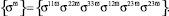

2. Преобразование узловых величин в точке на грани сочленения оболочек из разнородных материалов. Рассматриваются две произвольно нагруженные оболочки вращения в декартовых системах координат xyz и 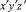. Связь между ортами этих систем считается известной (рис. 2)

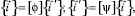(14)

где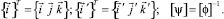

В узловой точке, расположенной на грани пересечения оболочек вращения, нужно найти зависимости между векторами примыкающей и основной оболочек соответственно

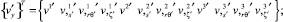(15)

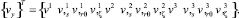(16)

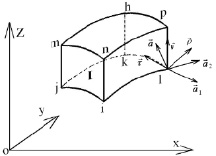
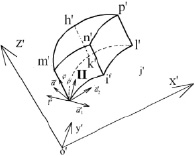
Рис. 2. Оболочки вращения в декартовых системах координат xoz и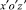

Для этого в узловой точке на заданной поверхности пересечения оболочек используется ортогональный базис 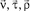, определенный через векторы базиса декартовых координат

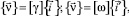(17)

где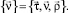

С использованием (4), (7) можно по (17) получить матричное соотношение

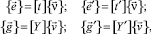(18)

где базисы

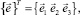
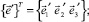
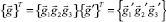
относятся соответственно к основной и примыкающей оболочкам.

Векторы 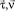лежат в плоскости грани пересечения, а вектор нормален к поверхности пересечения оболочек.

Для выполнения преобразований вводятся следующие промежуточные векторы узловой точки на грани пересечения, относящиеся к примыкающей и основной оболочкам

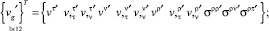(19)

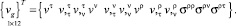(20)

Между векторами (19) и (20) записывается матричная зависимость

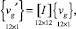(21)

где [I] – матрица, на главной диагонали которой элементы равны единице.

Для определения соотношений между компонентами векторов (20), (16) используются следующие условия.

1. Условие о равенстве векторов перемещений в базисах 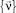и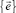

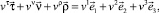
откуда с использованием (18) определяются компоненты 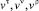через

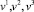
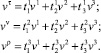(22)

Аналогично для примыкающей оболочки можно получить соотношения

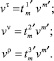(23)

2. Используется выражение производной скаляра a по направлению 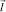в криволинейной ортогональной системе координат

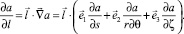(24)

На основании (24) можно записать выражения

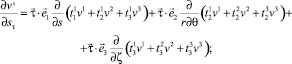
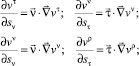
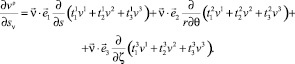(25)

Для примыкающей оболочки можно записать аналогичные соотношения

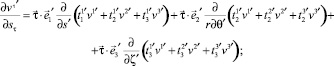
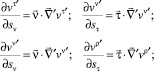
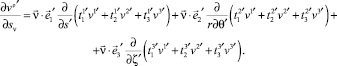(26)

Для тензора напряжений в различных базисах узловой точки границы пересечения оболочек имеют место соотношения

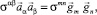(27)

где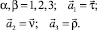

Используя соотношения (18), из (27) можно сформировать матричное выражение

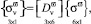(28)

где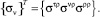

Принимая во внимание (13) и (15), можно выразить напряжения в базисе 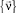через перемещения базиса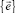

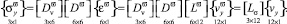(29)

Используя базис 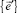примыкающей оболочки, можно получить матричное соотношение

(30)

На основании выражений (29), (30), (25), (26) формируются матричные соотношения

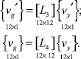(31)

Из условия равенства 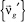и 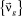получается

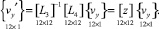(32)

С использованием (32) формируется матрица преобразования [Т] для матрицы жесткости и вектора узловых нагрузок граничного конечного элемента примыкающей оболочки

(33)

Пример № 1. Определялось напряженнo-деформированное состояние цилиндра со сферическим днищем, находящегося под действием внутреннего давления интенсивности q (рис. 3). Цилиндр и днище выполнены из разнородных материалов.

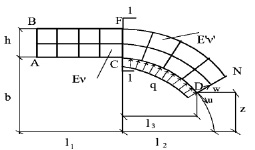
Рис. 3. Цилиндр со сферическим днищем под действием внутреннего давления интенсивности q

Были приняты следующие исходные данные: l1 = 0,2 м, l2 = 0,1 м, l3 = 0,09 м, q = 10 Н, h = 0,0005 м, b = 0,05 м, E = 2·105 МПа, ν = 0,3, E′ = 2·106 МПа, ν′ = 0,25.

Конструкция разбивалась на 10 конечных элементов по толщине, на 100 элементов по длине цилиндра и на 50 по дуге круговой оболочки.

По полученным результатам построена эпюра нормальных напряжений σxx (рис. 4) в сечении 1–1 (рис. 3). Условие равновесия по силам (ΣX = 0) правой части оболочки от сечения 1-1 выполняется с погрешностью δ = 0,6 %.

На основе анализа результатов выполненного примера расчета можно сделать вывод о корректности алгоритма определения напряженно-деформированного состояния в зонах сочленения оболочек вращения на основе разработанного конечного элемента [4].

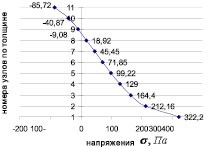
Рис. 4. Эпюра нормальных напряжений σxx в сечении 1–1 цилиндра со сферическим днищем

Рецензенты:

Голованов В.К., д.т.н., профессор кафедры «Начертательная геометрия и графика» ВГТУ, г. Волгоград;

Кукса Л.В., д.т.н., профессор, заведующий кафедрой «Сопротивление материалов», ВолГАСУ, г. Волгоград.

Работа поступила в редакцию 26.02.2014.

Библиографическая ссылка