Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

• Авторы
• Резюме
• Файлы
• Ключевые слова
• Литература

Жолудев С.Е. 1 Кандоба И.Н. 2

---

1 ГБОУ ВПО «Уральский государственный медицинский университет» Минздрава России

2 ФГАОУ ВПО «УрФУ имени первого Президента России Б.Н. Ельцина»

В данной работе приводятся результаты математического и численного моделирования напряженно-деформированного состояния (НДС) зубочелюстной системы (ЗЧС), включающей мягкие и костные ткани челюсти, а также восстановленный с помощью шинирующего дугового протеза зубной ряд. Основной целью такого исследования является построение методологии определения индивидуальной оптимальной формы одного из элементов дугового протеза – подкладочного слоя. Здесь под оптимальной формой подкладочного слоя понимается то рациональное распределение его толщины, которое позволяет минимизировать негативное влияние вертикальной нагрузки на ткани протезного ложа. Предлагается одна математическая модель такой задачи оптимизации формы подкладочного слоя. Эта модель относится к классу многокритериальных задач оптимизации области. В ней оптимизируемые критерии характеризуют как величины напряжений, так и равномерность их распределения на контактной границе «подкладка – мягкие ткани». Обсуждаются некоторые подходы к построению конструктивных методов решения исследуемой оптимизационной задачи. В частности, предлагается один численный алгоритм приближенного решения этой задачи, существенно учитывающий ее специфику. Этот алгоритм основан на использовании линейной выпуклой комбинации оптимизируемых критериев и применении специальных вариаций границы подкладочного слоя. Приводятся результаты вычислительных экспериментов с использованием реальных данных.

Статья в формате PDF

487 KB

дуговые протезы

эластическая подкладка

шинирование зубного ряда

математическое моделирование

численное моделирование

напряженно-деформированное состояние

оптимизация формы

1. Тарико О.С. Математическое обоснование применения подкладочного слоя в шинирующих дуговых протезах при заболеваниях пародонта, сочетающихся с концевыми дефектами зубного ряда / О.С. Тарико, С.Е. Жолудев, И.Н. Кандоба // Уральский медицинский журнал.  – 2010. – № 8(73). – С. 26–28.

2. Кандоба И.Н. Анализ напряженно-деформированного состояния в неоднородных конструкциях / И.Н. Кандоба, О.С. Тарико, Л.Ф. Спевак // Программные продукты и системы // Международный журнал. – 2012. – № 1. –С. 69–75.

3. Чумаченко Е.Н., Арутюнов С.Д., Лебеденко И.Ю. Математическое моделирование напряженно-деформированного состояния зубных протезов. – М.: МГМСУ, 2003. – 273 с.

4. Чуйко А.Н., Шинчуковский И.А. Биомеханика в стоматологии. – Харьков: Изд-во «Форт», 2010. – 466 с.

5. Чуйко А.Н., Вовк В.Е. Особенности биомеханики в стоматологии. – Харьков: Изд-во «Прапор», 2006. – 300 с.

6. Создание научных основ, разработка и внедрение в клиническую практику компьютерного моделирования лечебных технологий и прогнозов реабилитации больных с челюстно-лицевыми дефектами и стоматологическими заболеваниями / В.Н. Олесова, С.Д. Арутюнов, А.И. Воложин, Т.И. Ибрагимов и др.. – М.: МГМСУ, 2010. – 143 с.

7. Влияние циклической нагрузки на свойства эластичных материалов для мягких прокладок съемных протезов / В.Г. Чайка, Л.Н. Мунтян, А.В. Тимошенко, В.В. Коваль // Современная стоматология. – 2013. – № 2. – С. 82–85.

8. Подиновский В.В., Ногин В.Д. Парето-оптимальные решения многокритериальных задач. – М.: Наука, 1982. – 256 с.

9. Лурье А.К. Оптимальное проектирование в задачах математической физики. – М.: Наука, 1975. – 250 c.

10. Кандоба И.Н. Оптимизация формы накладки (pinlay). Моделирование упруго-напряженного состояния зуба / И.Н. Кандоба, П.А. Коледа, С.Е. Жолудев // Проблемы стоматологии. – 2007. – № 5. – С. 19–23.

Во многих клинических случаях у пациентов с заболеваниями пародонта врачу- ортопеду приходится проводить планирование конструкции зубных протезов таким образом, чтобы не только восполнить уже отсутствующие зубы, но и провести шинирование сохранившихся элементов зубного ряда. Актуальной проблемой, возникающей при практической реализации такого подхода, является уменьшение негативного воздействия на ткани протезного ложа жевательной нагрузки и увеличение жизненного цикла протеза. Одним из способов решения этой проблемы является использование мягких подкладок между базисом протеза и подлежащей слизистой оболочкой [1].

1. Математическая модель и напряженно-деформированное состояние системы «зубы-протез-челюсть»

ЗЧС может рассматриваться как неоднородная конструкция, подверженная воздействию заданной внешней статической нагрузки. Эта конструкция представляет собой объединение конечного числа упругих однородных сегментов, обладающих различными механическими свойствами. При этом можно считать, что часть внешней границы конструкции жестко закреплена, а к другой ее части прикладывается нагрузка. В этих условиях применение математического аппарата механики сплошной среды позволяет описать распределение напряжений и деформаций в сегментах указанной конструкции с помощью решения краевой задачи для системы дифференциальных уравнений [2, 3].

В исследуемой ситуации особый интерес представляет распределение напряжений и деформаций, возникающих на контактных границах сегмента, соответствующего подкладочному слою. Поскольку воздействие жевательной нагрузки на слизистую оболочку протезного ложа определяется в основном значениями напряжений и деформаций в несущем (фронтальном) сечении протеза и подкладочного слоя, то здесь можно ограничиться рассмотрением плоской неоднородной упругопластической задачи. Решение этой задачи позволяет провести требуемый анализ распределения напряжений и деформаций на контактной границе сегмента подкладочного слоя.

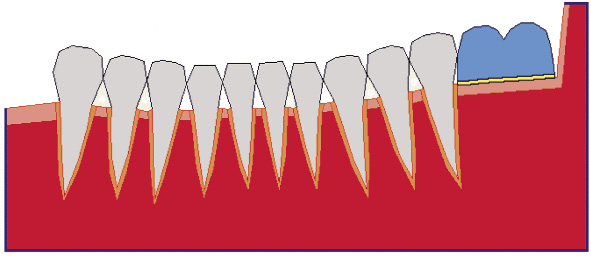
Рис. 1. Геометрическая модель фрагмента плоского сечения ЗЧС. Сегменты различных тканей ЗЧС и дугового протеза.

На рис. 1 представлена геометрическая модель фронтального (плоского) сечения фрагмента ЗЧС, построенная на основе рентгенограммы конкретного пациента. На рис. 1, 2, 3 серым цветом отображены сегменты твердых тканей зуба; розовым – сегменты слизистой оболочки; оранжевым – сегменты периодонта; красным – сегменты губчатой кости; светло-голубым – сегмент седловидной части дугового протеза (далее, для краткости, просто – протеза); желтым – сегмент подкладочного слоя.

Механические свойства всех образующих рассматриваемую неоднородную конструкцию однородных сегментов описываются двумя параметрами – модулем Юнга (μ) и коэффициентом Пуассона (v). Значения этих параметров для различных тканей и материалов индивидуальны. Здесь губчатая кость рассматривается как однородный материал, т.е. считается, что в ней расстояния между включениями во много раз больше размеров этих включений. Значения модуля Юнга и коэффициента Пуассона для различных тканей ЗЧС и материалов приведены в табл. 1. Часть этих данных взята из [3, 4, 5, 10], остальные данные были получены опытным путем. Так, значения упругих параметров пластмассы горячей полимеризации Vertex (материал седловидной части протеза) и материала подкладочного слоя (Mucopren Sof) были получены в результате испытаний по сертифицированной методике образцов этих материалов на универсальной испытательной машине Zwick Z2.5 в Институте машиноведения Уральского Отделения РАН.

Таблица 1

Значения модуля Юнга и коэффициента Пуассона для различных тканей ЗЧС и материалов

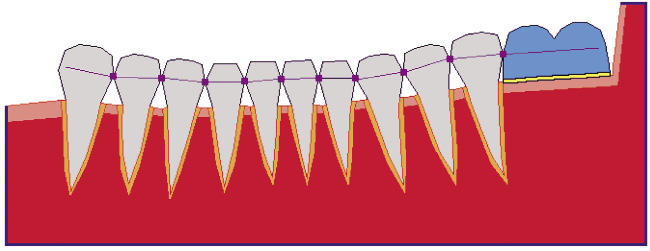
Рис. 2. Моделирование проволочной шины (ломаная линия фиолетового цвета)

Рис. 3. Фрагмент модели плоского сечения ЗЧС. Моделирование функциональной статической нагрузки

Моделирование шин различных типов в рамках плоской геометрической модели плоского сечения фрагмента ЗЧС осуществляется путем создания контактных точек (отрезков) контуров соседних сегментов твердых тканей зубов и сегмента протеза. В частности, шинирование зубного ряда с помощью проволочной шины в геометрической модели ЗЧС описывается набором контактных точек у границ сегментов, соответствующих соединенным шиной зубам и протезу (см. рис. 2). При этом замкнутые ломаные, определяющие границы плоских сечений любой пары соседних зубов и пары зуб-протез, имеют одну общую точку. На рис. 2 маркерами фиолетового цвета указаны контактные точки элементов зубного ряда, объединенных с помощью шины. Далее считается, что в этих точках отсутствуют относительные сдвиги контактирующих сегментов.

Функциональная жевательная нагрузка, прилагаемая через зубы и протез, передается через периодонт на губчатую кость и через подкладочный слой на слизистую оболочку протезного ложа. Такое воздействие на зубы и протез моделируется с помощью внешней статической нагрузки, задаваемой набором внешних сил, приложенным к внешней части контуров сегментов твердых тканей зубов и сегмента протеза. Для каждой силы указывается направление, серединная точка элементарной площадки приложения, величина силы и длина элементарной площадки приложения силы (см. рис. 3). При этом предполагается, что на внешнем контуре сегмента губчатой кости (на рис. 1–3 отображена темно-синим цветом) отсутствуют какие-либо смещения – эта граница жестко закреплена, а на контактных границах смежных сегментов отсутствуют относительные сдвиги. Эти данные позволяют однозначно задать граничные условия для системы дифференциальных уравнений, решение которой описывает НДС плоского сечения исследуемого фрагмента ЗЧС [2].

2. Задача оптимизации формы подкладочного слоя. Методы решения

Содержательно задача оптимизации формы подкладочного слоя заключается в следующем. Фиксируются вариант шинирования зубного ряда, форма седловидной части протеза, жевательная нагрузка на зубы и протез, значения упругих параметров материала подкладочного слоя. Требуется определить форму подкладочного слоя (распределение его толщины), для которой напряжения, возникающие на контактной границе «подкладка-слизистая», будут, во-первых, минимальны и, во-вторых, наиболее равномерно распределены на этой контактной границе. Существует мнение [7], что выполнение этих требований позволяет значительно уменьшить негативное влияние вертикальной нагрузки на слизистую оболочку протезного ложа.

Сформулируем математическую постановку этой оптимизационной задачи. Зафиксируем геометрическую форму однородных упругих сегментов (твердые ткани зубов, периодонт, слизистая, губчатая кость, седловидная часть протеза), образующих неоднородную конструкцию. С помощью заранее определенного набора контактных точек для контуров сегментов смежных зубов и протеза зафиксируем способ шинирования зубного ряда. Зададим на части внешней границы сегментов зубов и протеза напряжения моделирующие один из возможных вариантов воздействия жевательной нагрузки на восстановленный с помощью такого протеза зубной ряд.

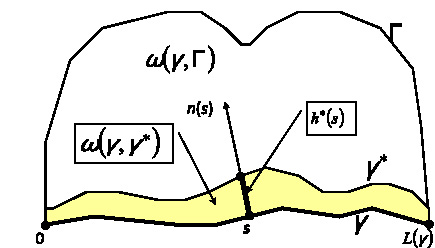
Рис. 4. Несущее плоское сечение седловидной части дугового протеза

Рассмотрим сегмент ω(γ, Γ) плоского сечения седловидной части протеза (рис. 4), где через γ и Γ обозначены контактная граница этого сегмента с сегментом слизистой оболочки и его внешняя граница соответственно. На контуре γ зададим натуральный параметр s ∈ [0, L(γ)], где L(γ) – длина контура γ. На отрезке [0, L(γ)] определим некоторую гладкую функцию h*(s). Для каждого s ∈ [0, L(γ)] значение этой функции h*(s) полагается равным длине отрезка, расположенного на внутренней к ω(γ, Γ) нормали n(s) к контуру γ в точке s (см. рис. 4). Такая функция h*(s) в свою очередь определяет некоторый гладкий контур γ*, который совместно с γ ограничивает дополнительный сегмент ω(γ, γ*), соответствующий подкладочному слою. Здесь контур γ* определяет форму этого подкладочного слоя, где функция h*(s) s ∈ [0, L(γ)] описывает распределение его толщины. Зафиксируем контуры γ, Γ и положительную величину P < mes(ω(γ, Γ)), где mes(ω(γ, Γ)) – площадь сегмента ω(γ, Γ). Зададим в точках контура Γ напряжения f, значения которых определяются внешней статической нагрузкой. Задача оптимизации заключается в определении такой гладкой функции h*(s), s ∈ [0, L(γ)], для которой выполняются следующие условия:

I) (1)

где mes(ω(γ, Γ)) – площадь сегмента ω(γ, γ*);

II) При замене части сегмента ω(γ, Γ) дополнительным сегментом ω(γ, γ*) обеспечивается одновременное достижение минимальных значений следующих критериев:

(2)

II) (3)

Здесь значение критерия V(h*) определяет среднее значение напряжения f на контактной границе γ, а значение критерия G(h*) – среднее значение разброса значений напряжений на этой границе. При некоторых достаточно адекватных реальности предположениях относительно свойств контура γ одновременная минимизация критериев (2) и (3) позволяет совместно минимизировать и напряжения, и добиваться наиболее равномерного распределения их значений на γ – контактной границе «подкладка-слизистая». При этом условие (1) накладывает ограничение на площадь допустимого плоского сечения прокладочного слоя, т.е. ограничение на объем материала этого слоя. Отсутствие этого ограничения приводит либо к полной замене материала седловидной части протеза материалом подкладочного слоя, либо к возникновению недопустимой подвижности седловидной части протеза.

С точки зрения математической, задача (I, II) относится к классу многокритериальных задач оптимизации конструкций. Как правило, в многокритериальных задачах удается найти лишь некоторое компромиссное решение, например, оптимальное по Парето решение [8].

Один из подходов к решению многокритериальной задачи заключается в переходе от такой оптимизационной задачи (I, II) к задаче минимизации при ограничении (1) одного критерия

III) (4)

где α ∈ [0, 1] – числовой параметр, определяющий приоритеты при минимизации критериев (2) и (3) – чем ближе значение параметра α к нулю, тем больший приоритет отдается достижению наиболее равномерного распределения напряжений на контактной границе «подкладка-слизистая», чем ближе к единице – минимизации среднего значения напряжений на этой границе. При α = 0,5 формируются в некотором смысле паритетные условия для одновременной минимизации обоих критериев (2) и (3).

Так как форма конструкции (подкладочного слоя) описывается функцией h*(s), то для минимизации критерия (4) могут быть использованы методы, изложенные в [9]. Кроме того, здесь для минимизации критерия (4) могут быть применены и подходы, основанные на использовании специальных вариаций (изменений) оптимизируемой границы γ* [10]. Последовательное применение этих вариаций позволяет построить близкий к оптимальному контур γ* (функцию h*(s), описывающую оптимальное распределение толщины подкладочного слоя). На этом контуре (функции) при подходящем выборе значения параметра α достигается практически минимальное значение критерия (4). В данном случае упомянутые вариации границы γ* достаточно просто могут быть построены аналитически:

(5),

где n(s) – единичный вектор внутренней к ω(γ, Γ) нормали к контуру γ в точке s ∈ [0, L(γ)] (см. рис. 5); ε – масштабирующий коэффициент вариации. Здесь изопериметрическое ограничение (1) при вариации (5) выполняется в силу очевидного равенства

Здесь сходимость последовательности контуров, приближающей оптимальный контур γ*, обеспечивается за счет последовательного уменьшения значений масштабирующего коэффициента ε вариации (5).

3. Результаты численного моделирования. Анализ результатов

Вычислительные эксперименты проводились с помощью специализированного программного обеспечения «НДС-ОПТИМА» (Свидетельство о государственной регистрации программы для ЭВМ № 2011613416 от 29.04.2011) [2].

Для построения геометрической модели фронтального сечения фрагмента ЗЧС (см. рис. 1, 2) использовалась рентгенограмма реального пациента. Предполагалось, что все зубы ряда шинируются с помощью шины из проволоки флекс. При этом рассматривались несколько возможных вариантов направлений и точек приложения внешних сил. Эти варианты обусловливаются особенностями механизмов функционирования зубочелюстной системы. На рис. 3 представлен один из возможных вариантов воздействия внешней нагрузки в виде набора векторов внешних сил. Здесь для каждого вектора указаны параметры соответствующей силы – величина силы и длина элементарной площадки ее приложения.

Результаты численного решения описанной выше оптимизационной задачи позволяют сделать следующий вывод. Использование подкладочного слоя и конструирование формы его плоского сечения с использованием оптимальной функции h*(s) (см. рис. 4), решения однокритериальной оптимизационной задачи (III) позволяет существенно уменьшить на контактной границе «подкладка-слизистая» как напряжения, так и величину разброса их значений. В отдельных случаях путем выбора значения параметра α в критерии (4) удается за счет рационального выбора формы плоского сечения подкладочного слоя существенно уменьшить значения обоих критериев (2) и (3) по сравнению с ситуацией, когда подкладочный слой распределен равномерно (h*(s) ≡ const).

Таблица 2

Результаты оптимизации формы подкладочного слоя

а б

Рис. 5. Результаты оптимизации формы подкладочного слоя: а – начальное (равномерное –h*(s) ≡ const) распределение толщины слоя; б ‒ близкое к оптимальному распределение толщины слоя (h*(s) ≠ const)

В табл. 2 приведены результаты оптимизации формы подкладочного слоя. В этой таблице содержатся данные о минимальном (f_min), максимальном (f_max) значениях напряжений, возникающих на контактной границе «подкладка-слизистая», а также – их разности (fmax – f_min). В первой строке таблицы указаны перечисленные данные о напряжениях для случая, когда подкладочный слой распределен равномерно (имеет фиксированную толщину – h*(s) ≡ const, s ∈ [0, L(γ)]) (рис. 5(а)). Во второй строке – для случая, когда материал подкладочного слоя специальным образом перераспределен (рис. 5(б)). В обоих случаях площадь P сегмента, соответствующего подкладочному слою, одна и та же.

Здесь в результате решения задачи минимизации критерия (4) при α = 0,5 удается определить достаточно близкое к оптимальному распределение толщины подкладочного слоя. За четыре последовательных вариации (5) границы γ* удается на 25 % уменьшить максимальное значение напряжения и на 17 % понизить значение разности максимального и минимального значений напряжений на контактной границе «подкладка-слизистая» (табл. 2). При этом изменение значения α = 0,5 приводит к тому, что на контактной границе «подкладка-слизистая» либо значительно увеличиваются значения напряжений «в целом», либо существенно увеличивается их разброс.

Заключение

Результаты вычислительных экспериментов с использованием реальных данных свидетельствуют, что форма фронтального плоского сечения подкладочного слоя в шинирующем дуговом протезе является тем ресурсом, за счет рационального или оптимального использования которого можно добиться значительного снижения негативного воздействия функциональной жевательной нагрузки на слизистую оболочку протезного ложа.

Работа выполнена в рамках программ фундаментальных исследований Президиума РАН «Динамические системы и теория управления» при поддержке УрО РАН (проект 12-П-1-1022), (проект 13-1-006-НПО), «Информационные, управляющие и интеллектуальные технологии и системы» (проект 12-П-1-1023).

Мандра Ю.В., д.м.н., доцент, декан стоматологического факультета, ГБОУ ВПО УГМУ МЗ РФ, г. Екатеринбург;

Григорьев С.С., д.м.н., доцент, доцент кафедры пропедевтики и физиотерапии стоматологических заболеваний ГБОУ ВПО УГМУ МЗ РФ, г. Екатеринбург.

Работа поступила в редакцию 26.03.2014.

Библиографическая ссылка