Научный журнал

Фундаментальные исследования

ISSN 1812-7339

"Перечень" ВАК

ИФ РИНЦ = 1,674

Решение задач моделирования ТС необходимо выполнять с позиций теории ДС и системного анализа. Параметры математических моделей (ММ) ТС, как правило, неизвестны и могут быть оценены посредством анализа экспериментальных данных – реакций ТС, которые являются функционалами от искомых параметров. Такая взаимосвязь в теории линейных систем описывается интегральным уравнением Винера-Хопфа, связывающим автокорреляционную функцию стационарного случайного процесса (СП) на входе объекта, взаимнокорреляционную функцию СП на выходе и входе объекта с весовой функцией системы.

Постановка задачи в такой форме приводит к возникновению проблемы идентификации ДС. Понятие идентификации в данном случае тесно связано с понятием неопределенности. Одним из видов классификации неопределенности является классификация по её характеру. Она включает в себя два больших класса неопределенности: параметрическая и структурная. Для широкого класса задач в машиностроении априорная неопределенность может быть сведена к параметрической неопределенности, которая подразумевает, что математические зависимости, описывающие наблюдаемые процессы, известны с точностью до конечного числа параметров. В таком случае исследуемой ТС можно управлять на основе статичной программы, опирающейся лишь на априорную информацию о системе, или на основе применения принципа обратной связи, позволяющего уменьшить существующую априорную неопределенность. Второй из указанных подходов предполагает необходимость наблюдений за системой в течение всего процесса управления.

Таким образом, при известной структуре ММ задача идентификации сводится к так называемой параметрической идентификации, заключающейся в оценивании параметров рассматриваемой ММ исследуемой ТС.

Многие задачи параметрической и непараметрической идентификации ДС, обработки экспериментальных данных и численного анализа относятся к классу так называемых некорректно поставленных задач.

Характерной чертой таких задач является неустойчивость их решения: малые изменения исходных данных могут вызвать произвольно большие изменения решений, т.е. погрешность в исходных данных может играть принципиальную роль. Эта неустойчивость при наличии погрешностей в данных приводит к тому, что решение не будет единственным, а также возникнут трудности в выяснении смысла полученного решения. Поэтому методы устойчивого решения некорректных задач имеют не только теоретическую, но и большую практическую значимость.

Для решения задач такого рода может быть использованы два основных подхода. Первый подход заключается в доопределении априорной информации для исключения неопределенности и получения возможности решить корректно поставленную задачу одним из численных методов. Второй подход подразумевает применение методов регуляризации. Основная идея метода регуляризации заключается в сужении класса функций, среди которых идет поиск решения. Решение некорректных задач невозможно без привлечения дополнительной априорной информации, играющей в таком случае ключевую роль. Существует непосредственная связь между количеством такой априорной информации и устойчивостью алгоритма решения: чем большей априорной информацией мы обладаем, тем более устойчивые алгоритмы могут быть использованы при решении.

Поэтому привлекательными являются методы, которые позволяют решать поставленную некорректную задачу при наличии минимальной априорной информации. Одним из эффективных методов приближенного решения таких задач является метод регуляризации Тихонова, в основе которого лежит понятие регуляризующего алгоритма.

Для интегрального уравнения типа свертки вида (1) с использованием метода Тихонова определяется такое регуляризированное решение , которое минимизирует функционал (2):

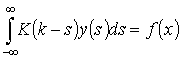              (1)

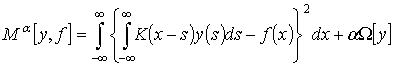,            (2)

где для регуляризации -го порядка

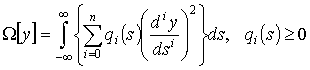.             (3)

Следует отметить, что одним из наиболее сложных этапов в методах регуляризации справедливо считается определение параметра регуляризации . При решении этой задачи необходимо определить такое значение, которое, с одно стороны, являясь немалым, делало бы решение уравнения устойчивым, а с другой стороны, являясь небольшим, не сильно искажало бы первоначальное решение уравнения.

Таким образом, применение методов регуляризации при идентификации и моделировании ТС позволяет получить решение поставленных задач в условиях малой априорной информации и некорректно поставленной исходной задачи.

СПИСОК ЛИТЕРАТУРЫ:

1. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1979, 248 с.
2. Тихонов А.Н., Гончаровский А.В., Степанов В.В., Ягола А.Г. Численные методы решения некорректных задач. – М.: Наука, 1990, 230 с.
3. Современные методы идентификации / Под ред. П. Эйкхоффа. – М.: Мир, 1983, 400 с.