Реальные инвестиции обычно связаны со значительными затратами и во многом определяют будущее предприятия, что обусловливает исключительную важность их оптимального выбора и принадлежность к стратегическим задачам верхнего уровня системы управления предприятием [8]. Процесс выбора проектов и распределения ресурсов включает определение, какие из проектов следует принять, и оптимальное распределение ограниченных ресурсов между несколькими проектами, претендующими на имеющиеся ресурсы [6]. Задача осложняется следующими обстоятельствами [9]: каждый проект подвержен рискам и неопределенности; возможно наличие нескольких, часто конфликтующих целей; некоторые из этих целей могут быть заданы в качественной форме; выбор должен быть сбалансирован с учетом важности многочисленных факторов; некоторые проекты могут быть взаимозависимыми; число потенциальных проектов может быть очень велико. В настоящей статье мы рассматриваем некоторые аспекты первой из этих проблем.
Для задачи принятия инвестиционных решений необходимо установить приоритеты, позволяющие упорядочить потенциально возможные проекты. Эти приоритеты могут оцениваться на основе различных критериев, как экономических, так и стратегических [10]. Наиболее значимой является оценка экономической эффективности проектов, общепринятые методы определения которой основаны на классическом анализе денежных потоков. Предпочтительным критерием для сравнения альтернативных проектов является чистый приведенный доход (NPV), так как критерий внутренней нормы рентабельности (IRR), несмотря на его широкое применение в качестве показателя эффективности инвестиций, имеет серьезные недостатки [5]. Однако, в свою очередь, при расчете NPV возникают проблемы с определением ставки дисконтирования.
Расчет NPV выполняется на основании прогнозных денежных потоков, номинальные значения которых для каждого периода времени умножаются на соответствующий коэффициент дисконтирования:
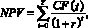
где CF(t) – номинальный суммарный денежный поток в период t; t – порядковый номер периода проекта; T – горизонт планирования проекта; r – ставка дисконтирования (норма дисконта).
Ставка дисконтирования является экзогенно задаваемым основным экономическим нормативом, используемым при оценке эффективности проекта, и отражает максимальную доходность альтернативных и доступных направлений инвестирования и темп падения ценности денег [3].
Главная проблема оценки проектов связана с отсутствием однозначного теоретического и практического метода решения проблем неопределенности [1]. Принятие решений почти всегда происходит в условиях неполной информации. Неполная информация о предпочтениях, например, несколько лиц, принимающих решение, группы с разными интересами и неполная информация о наборе альтернатив определяются как важнейшие характеристики реального процесса принятия решений [7]. Невозможность точного определения параметров расчета сильно снижает достоверность оценок инвестиционных проектов. Это относится и к адекватному выбору ставки дисконтирования, значение которой существенно влияет на результат оценки. Понятно, что если оно занижено, то будет выбран на самом деле неэффективный проект; если завышено, то объективно эффективный проект будет отклонен [3]. Однако полной уверенности в значении принятой ставки дисконтирования обычно нет.
В литературе предлагаются различные способы определения ставки дисконтирования [3, 4]. Основным предметом дискуссий является добавление премии за риск. Прибавление рисковой премии к норме дисконта является наиболее распространенным способом учета неопределенности при выборе инвестиционных проектов. Этот подход критикуется в работе [4], автор которой доказывает теоретическую несостоятельность и серьезную практическую опасность введения в ставку дисконтирования премий за риск, что не только не приводит к адекватному учету экономических рисков, но и уводит в сторону от адекватного прогноза.
Если согласиться с тем, что добавлять премию за риск не следует, альтернативные проекты будут иметь одинаковые значения ставки дисконтирования. Если вводить премии за риск, то альтернативные проекты могут иметь разные значения ставки дисконтирования. Но и в этом случае существует большой класс задач, для которых дисконтирование денежных потоков всех проектов производится по единой ставке. Например, выбор варианта проекта из возможных альтернатив (которые можно рассматривать как различные проекты) на этапе исследования инвестиционных возможностей. Проект может быть реализован различными способами (например, с точки зрения его размещения, используемых технологий, приобретаемого оборудования и т.д.), из которых необходимо определить наилучший. Далее рассматривается именно такая ситуация, когда необходимо ранжировать набор альтернативных проектов, для оценки которых используется единая ставка дисконтирования.
В любом случае, как указывается в работе [2], на стадии разработки проекта норма дисконта может быть точно не известна, а предпочтения лица, принимающего решения, могут изменяться. Таким образом, возникает проблема сравнения проектов при неоднозначном задании ставки дисконтирования. В связи с этим мы предлагаем использовать интегральную оценку проектов по диапазону изменения величины нормы дисконта.
Формально постановку задачу можно представить в следующем виде. Имеется набор из P проектов. Для каждого проекта известны оценки величин чистого приведенного дохода в зависимости от значения ставки дисконтирования NPVk(r); r – ставка дисконтирования; k – номер проекта; k = 1, …, P. Необходимо ранжировать проекты по величинам чистого приведенного дохода при условии единой для всех проектов ставки дисконтирования, заданной интервалом возможных значений, отражающим предпочтения лица, принимающего решения.
На рис. 1 представлены зависимости чистого приведенного дохода от ставки дисконтирования для двух проектов i и j. Граничное значение rbnd разделяет возможные значения нормы дисконта на две области:
– при r > rbnd чистый приведенный доход больше для проекта i;
– при r < rbnd чистый приведенный доход больше для проекта j;
– при r = rbnd величины чистого приведенного дохода для обоих проектов равны.
Так как при реальной оценке инвестиционных проектов однозначно задать значение ставки дисконтирования затруднительно, уверенности в точном установлении этого значения нет, то, если оно должно быть близко к величине rbnd, значительно снижается и уверенность в объективном определении приоритетности проектов.
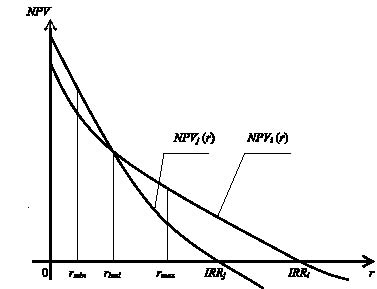
Рис. 1. Зависимости величин чистого приведенного дохода от ставки дисконтирования для проектов i и j
В то же время можно достаточно достоверно определить интервал [rmin, rmax], в пределах которого должно находиться это значение. В этом случае можно предложить адекватный способ сравнения проектов i и j с помощью интегрального показателя RNij, который рассчитывается следующим образом:
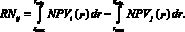
Тогда результат сравнения проектов определяется, исходя из величины этого интегрального показателя:
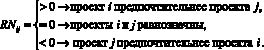
Проиллюстрируем процедуру сравнения проектов следующим реальным примером. В табл. 1 и 2 приведены прогнозные денежные потоки по двум планируемым вариантам реализации проекта модернизации предприятия, производящего строительные материалы. Варианты предполагают использование различного оборудования, отличающегося по стоимости, производительности и эксплуатационным издержкам.
Таблица 1
Денежные потоки по варианту 1 проекта (руб.)
|
Годы Номинальные денежные потоки |
1 |
2 |
3 |
4 |
5 |
|
Поступления от продаж |
6 116 364 |
10 679 772 |
11 543 246 |
12 697 571 |
13 967 328 |
|
Суммарные переменные издержки |
1 161 818 |
2 467 032 |
2 601 170 |
2 730 401 |
3 003 442 |
|
Суммарные постоянные издержки |
3 860 793 |
4 334 344 |
4 482 183 |
4 596 241 |
4 606 734 |
|
Налоги и отчисления |
541 787 |
1 164 697 |
1 249 850 |
1 401 149 |
1 512 319 |
|
Инвестиционные издержки |
8 800 000 |
– |
– |
– |
– |
На рис. 2 представлены зависимости величин чистого приведенного дохода от ставки дисконтирования для каждого варианта проекта. Оба варианта обеспечивают равное значение NPV1 = NPV2 = 1003980 руб. при норме дисконта rbnd = 18,41 %.
Таблица 2
Денежные потоки по варианту 2 проекта (руб.)
|
Годы Номинальные денежные потоки |
1 |
2 |
3 |
4 |
5 |
|
Поступления от продаж |
6 122 480 |
11 662 311 |
13 655 660 |
16 176 705 |
19 065 402 |
|
Суммарные переменные издержки |
1 124 639 |
2 605 185 |
2 975 738 |
3 363 854 |
396 4543 |
|
Суммарные постоянные издержки |
3 822 185 |
4 681 091 |
5 244 154 |
5 791 263 |
6 219 090 |
|
Налоги и отчисления |
530 409 |
1 243 896 |
1 446 076 |
1 745 831 |
2 018 945 |
|
Инвестиционные издержки |
11 616 000 |
– |
– |
– |
– |
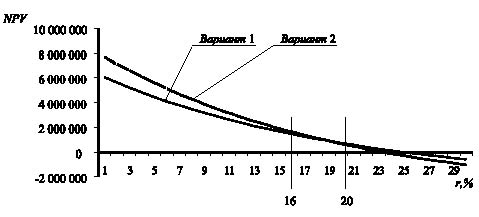
Рис. 2. Зависимости величин чистого приведенного дохода от ставки дисконтирования для двух вариантов проекта модернизации
При определении значений номы дисконта интервалом [rmin = 16 %, rmax = 20 %] интегральный показатель RN12 = 5435650 – 5567709 = – 132059. Так как RN12 < 0, вариант 2 проекта предпочтительнее варианта 1.
Подобным способом можно ранжировать и большее число проектов.
Рецензенты:Крутиков В.К., д.э.н., профессор, проректор по научно-методической работе, НОУ ВПО «Институт управления, бизнеса и технологий», г. Калуга;
Садковская Н.Е., д.т.н., профессор, ФГБОУ ВПО «Московский государственный технический университет имени Н.Э. Баумана», г. Калуга;
Роздольская И.В., д.э.н., профессор, заведующая кафедрой маркетинга и менеджмента Белгородского университета кооперации экономики и права, г. Белгород.
Работа поступила в редакцию 07.02.2014.
Библиографическая ссылка
Птускин А.С., Волков А.И. РАНЖИРОВАНИЕ ВАРИАНТОВ ИНВЕСТИЦИОННЫХ ПРОЕКТОВ ПРИ НЕОДНОЗНАЧНОМ ЗАДАНИИ СТАВКИ ДИСКОНТИРОВАНИЯ // Фундаментальные исследования. 2014. № 3-2. С. 340-343;URL: https://fundamental-research.ru/ru/article/view?id=33635 (дата обращения: 12.02.2026).



